問題:円と接線
次の問いに答えよ。
\({\small (1)}~\)円と直線が1点だけを共有するとき、
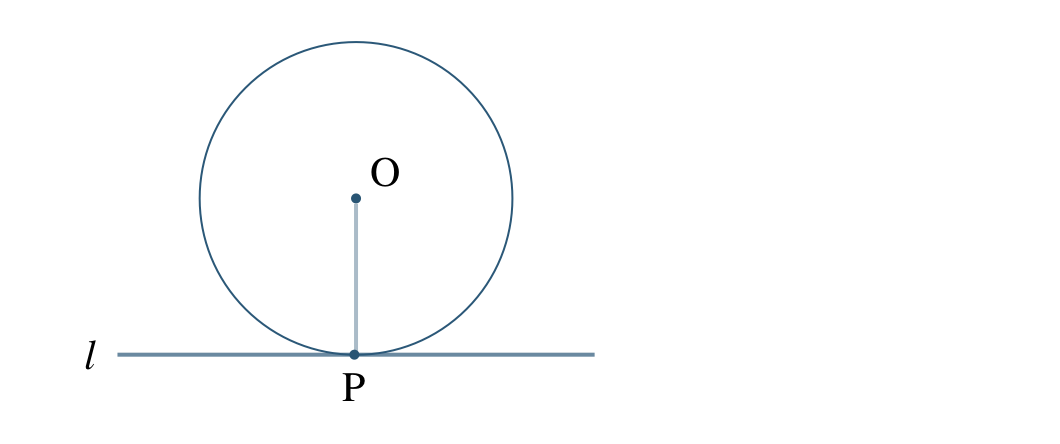
① この円 \({\rm O}\) と直線 \(l\) の関係は何というか答えよ。
② 直線 \(l\) を何というか答えよ。
③ 点 \({\rm P}\) を何というか答えよ。
④ 直線 \(l\) と半径 \({\rm OP}\) の関係を何というか答えよ。
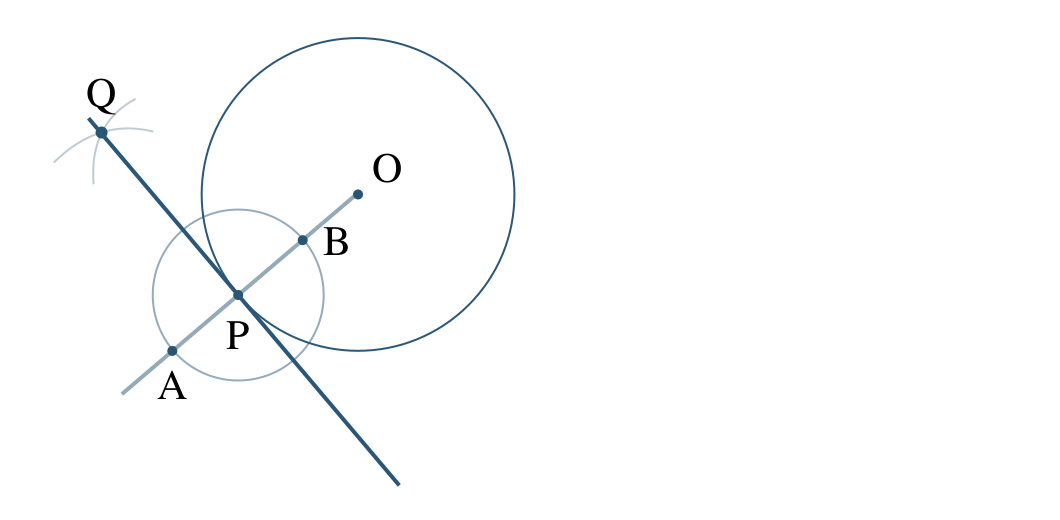
\({\small (2)}~\)次の図の点 \({\rm P}\) が接点となるように、接線を作図せよ。

解法のPoint
円と直線が1点だけを共有するとき、
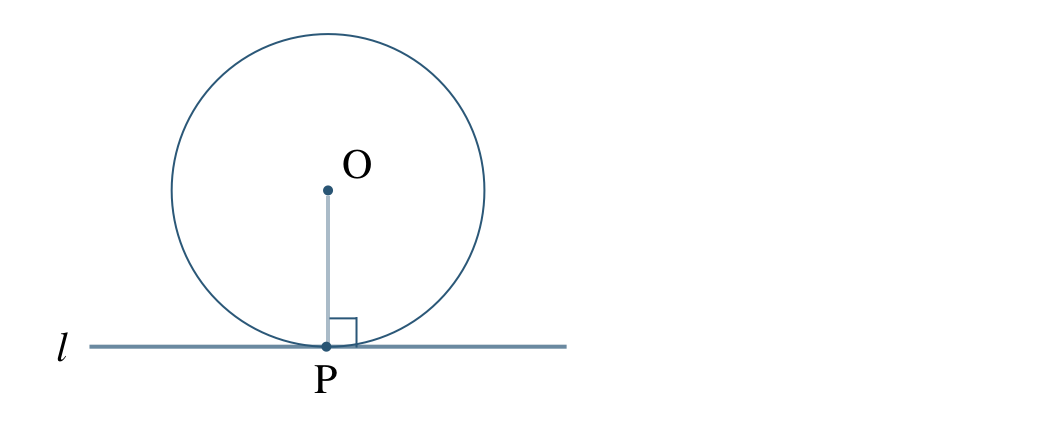
「直線は円に接する」といい、直線 \(l\) を円 \({\rm }\) の「接線」といい、点 \({\rm P}\) を「接点」という。
また、円の接線はその接点を通る半径に垂直である。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
円 \({\rm O}\) の円周上の点 \({\rm P}\) での接線の作図の方法は、
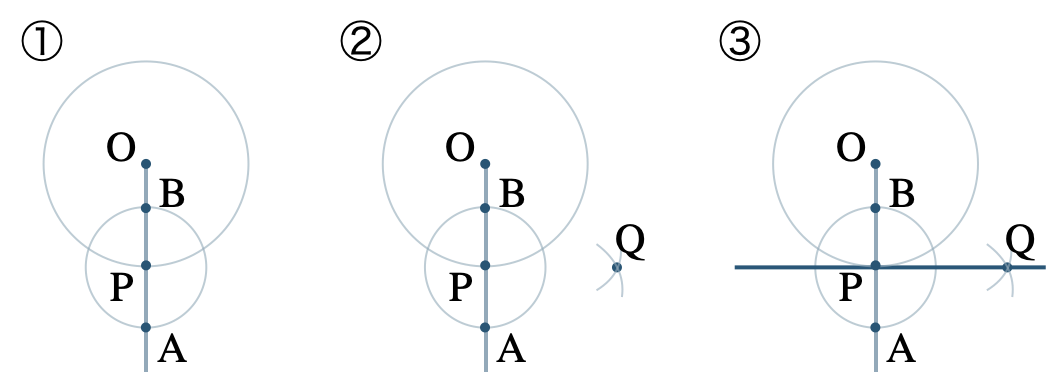
① 半直線 \({\rm OP}\) を引いて、点 \({\rm P}\) が中心の円をかき、半直線 \({\rm OP}\) との交点を \({\rm A~,~B}\) とする。
② 2点 \({\rm A~,~B}\) を中心とする等しい半径の円をかき、その交点を \({\rm Q}\) とする。
③ 直線 \({\rm PQ}\) が円 \({\rm O}\) の点 \({\rm P}\) での接線となる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:円と接線
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)円と直線が1点だけを共有するとき、

① この円 \({\rm O}\) と直線 \(l\) の関係は何というか答えよ。
② 直線 \(l\) を何というか答えよ。
③ 点 \({\rm P}\) を何というか答えよ。
④ 直線 \(l\) と半径 \({\rm OP}\) の関係を何というか答えよ。
① 円と直線は1点だけを共有するので、
直線 \(l\) は円 \({\rm O}\) に接する
となる
② 直線 \(l\) は円 \({\rm O}\) に接するので、
直線 \(l\) は接線
となる
③ 点 \({\rm P}\) は円と直線と共有しているので、
点 \({\rm P}\) は接点
となる
④ 接線 \(l\) は円 \({\rm O}\) に接するので、
接線 \(l\) は半径 \({\rm O}\) と垂直
となる
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)次の図の点 \({\rm P}\) が接点となるように、接線を作図せよ。

接線は、円 \({\rm O}\) の半径の接点 \({\rm P}\) における垂直となるので、
半直線 \({\rm OP}\) をひいて、点 \({\rm P}\) を中心の円をかき、半直線 \({\rm OP}\) との交点を \({\rm A~,~B}\) とする

2点 \({\rm A~,~B}\) をそれぞれ中心とする、半径の等しい円をかき、2つの円の交点を \({\rm Q}\) とする
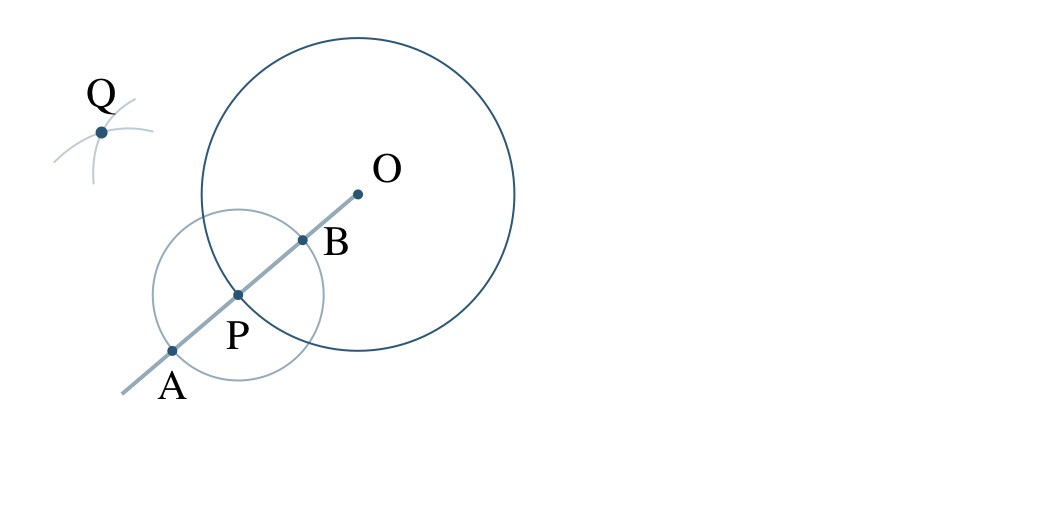
直線 \({\rm PQ}\) をひくと、これが円の接線となる