問題:面や線が動いてできる立体
問題
\({\small (1)}~\)次の立体は、どのような図形を動かしてできるものか答えよ。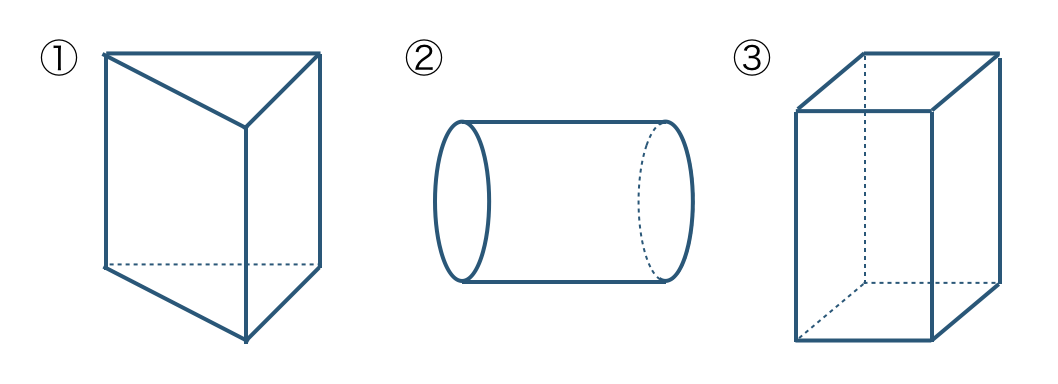
次の問いに答えよ。
\({\small (1)}~\)次の立体は、どのような図形を動かしてできるものか答えよ。

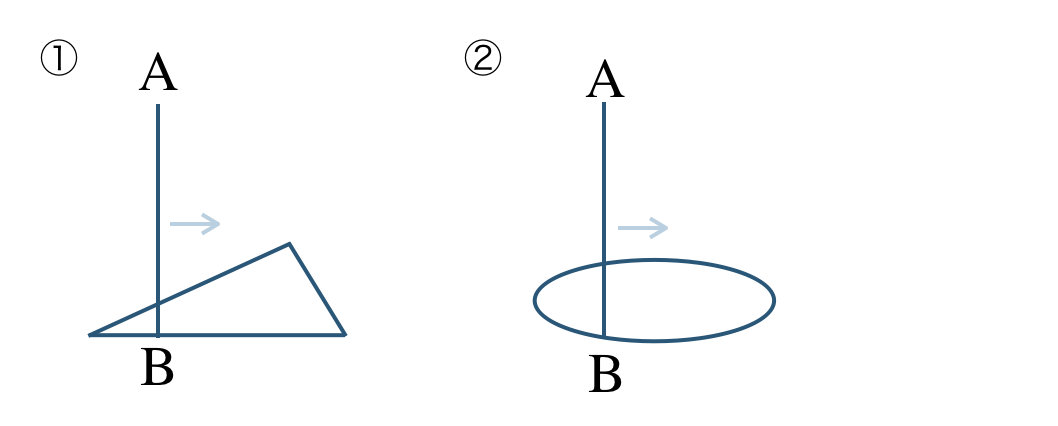
\({\small (2)}~\)次の平面上の図形の周にそって、垂直な直線 \({\rm AB}\) をひとまわり動かしてできる立体を答えよ。

解法のPoint
Point:面が動いてできる立体
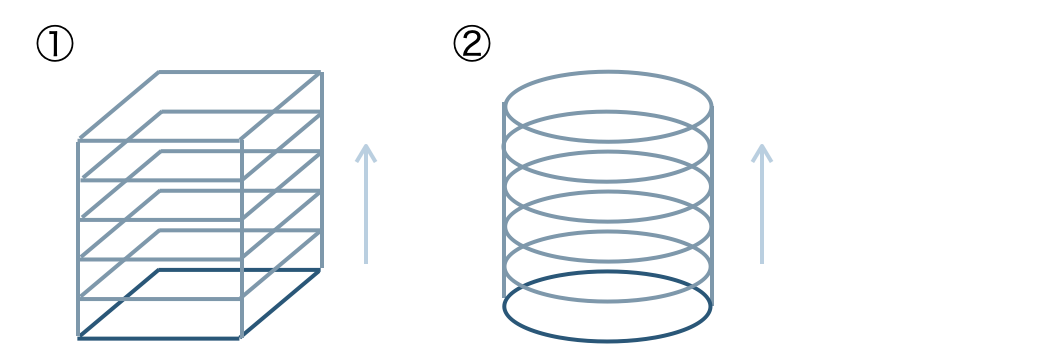
このとき、動いた距離が立体の高さとなる。
角柱や円柱は、多角形や円をその面に垂直な方向に動かしてできる立体と見ることができる。

① 四角形を動かすと、四角柱となる
② 円を動かすと、円柱となる
このとき、動いた距離が立体の高さとなる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
Point:線が動いてできる立体
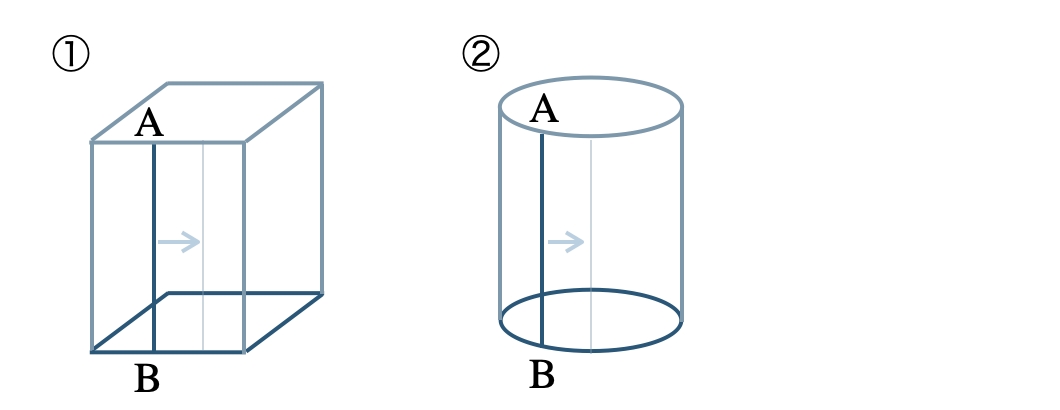
このとき、線分 \({\rm AB}\) を「母線」という。
角柱や円柱は、多角形や円柱に垂直な線分 \({\rm AB}\) をその周にそって、ひとまわりさせてできた立体と見ることができる。

① 四角形の周りを動かすと、四角柱となる
② 円の周りを動かすと、円柱となる
このとき、線分 \({\rm AB}\) を「母線」という。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:面や線が動いてできる立体
問題解説(1)
問題
\({\small (1)}~\)次の立体は、どのような図形を動かしてできるものか答えよ。
次の問いに答えよ。
\({\small (1)}~\)次の立体は、どのような図形を動かしてできるものか答えよ。

① この三角柱の底面は三角形てあるので、
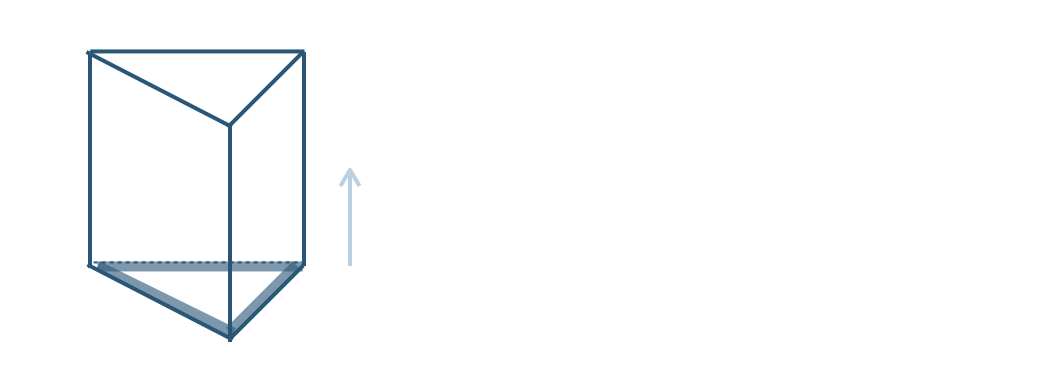
よって、
三角形を動かしてできる立体 となる
② この円柱の底面は円てあるので、

よって、
円を動かしてできる立体 となる
③ この四角柱の底面は四角形てあるので、

よって、
四角形を動かしてできる立体 となる
問題解説(2)
問題
\({\small (2)}~\)次の平面上の図形の周にそって、垂直な直線 \({\rm AB}\) をひとまわり動かしてできる立体を答えよ。
次の問いに答えよ。
\({\small (2)}~\)次の平面上の図形の周にそって、垂直な直線 \({\rm AB}\) をひとまわり動かしてできる立体を答えよ。

① 直線 \({\rm AB}\) を母線として、三角形の周をひとまわり動かすと、

これより、三角柱 となる
② 直線 \({\rm AB}\) を母線として、円の周をひとまわり動かすと、

これより、円柱 となる

【問題一覧】中1|空間図形
このページは「中学数学1 空間図形」の問題一覧ページとなります。解説の見たい単元名がわからないときは...


