問題:グラフから1次関数の式を求める
問題
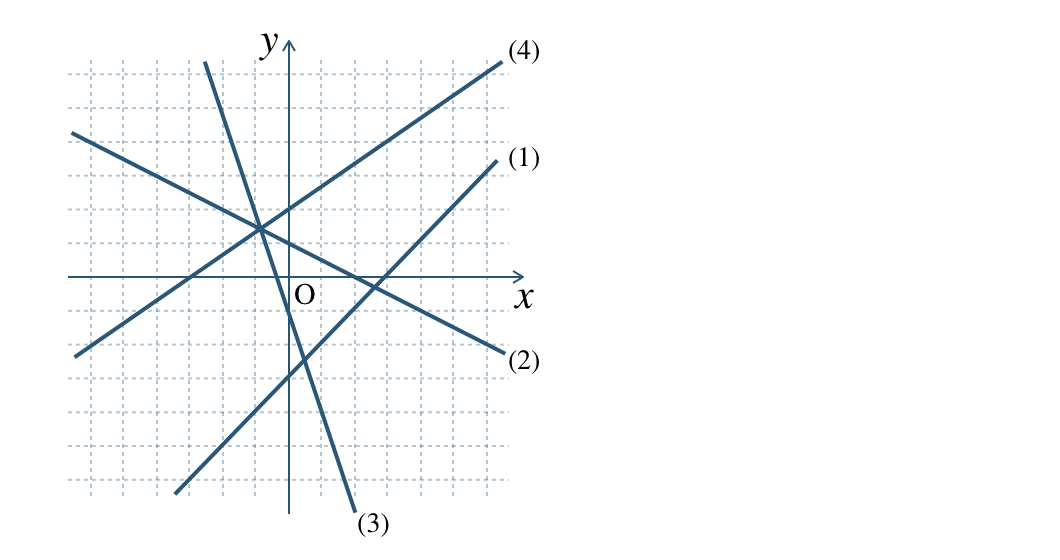
次の図の (1) 〜 (4) の直線の式を求めよ。

解法のPoint
Point:グラフから1次関数の式を求める
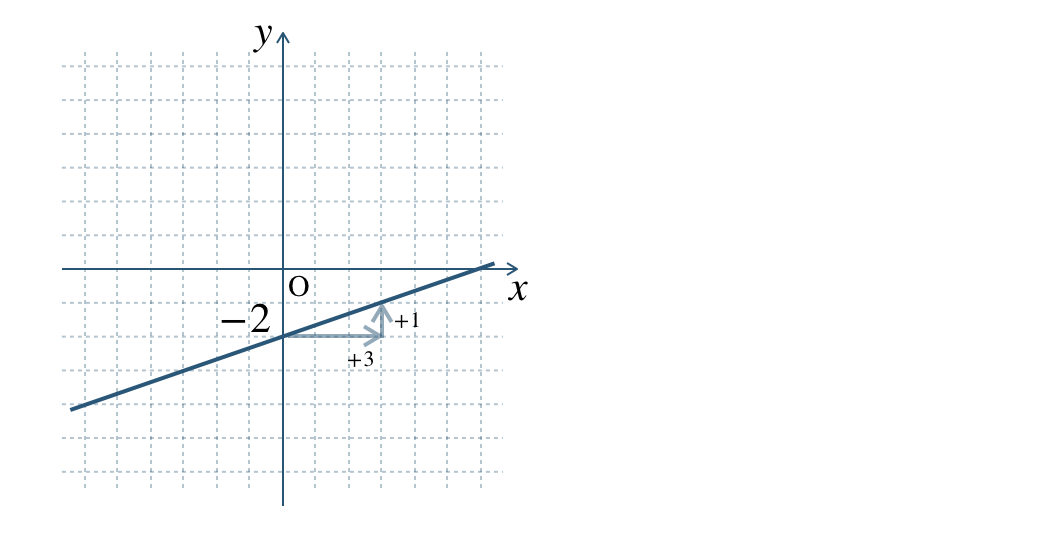
グラフより、\(y\) 軸との交点 \((0~,~-2)\) であり、
切片 \(b=-2\) となる
② 切片とは別の読みとりやすい点をとり、\(x\) の増加量と \(y\) の増加量から傾き \(a\) を求める。
\(x\) の増加量 \(3\) 、 \(y\) の増加量 \(1\) で、傾き \(\begin{split}{\frac{\,1\,}{\,3\,}}\end{split}\)
③ 1次関数の式 \(y=ax+b\) を求める。
\(\begin{split}b=-2~,~a={\frac{\,1\,}{\,3\,}}\end{split}\) より、\(\begin{split}y=\frac{\,1\,}{\,3\,}x-2\end{split}\)
グラフから1次関数の式の求め方は、

① \(y\) 軸との交点 \((0~,~b)\) から切片 \(b\) を読みとる。
グラフより、\(y\) 軸との交点 \((0~,~-2)\) であり、
切片 \(b=-2\) となる
② 切片とは別の読みとりやすい点をとり、\(x\) の増加量と \(y\) の増加量から傾き \(a\) を求める。
\(x\) の増加量 \(3\) 、 \(y\) の増加量 \(1\) で、傾き \(\begin{split}{\frac{\,1\,}{\,3\,}}\end{split}\)
③ 1次関数の式 \(y=ax+b\) を求める。
\(\begin{split}b=-2~,~a={\frac{\,1\,}{\,3\,}}\end{split}\) より、\(\begin{split}y=\frac{\,1\,}{\,3\,}x-2\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:グラフから1次関数の式を求める
問題解説(1)
問題

次の図の (1) 〜 (4) の直線の式を求めよ。

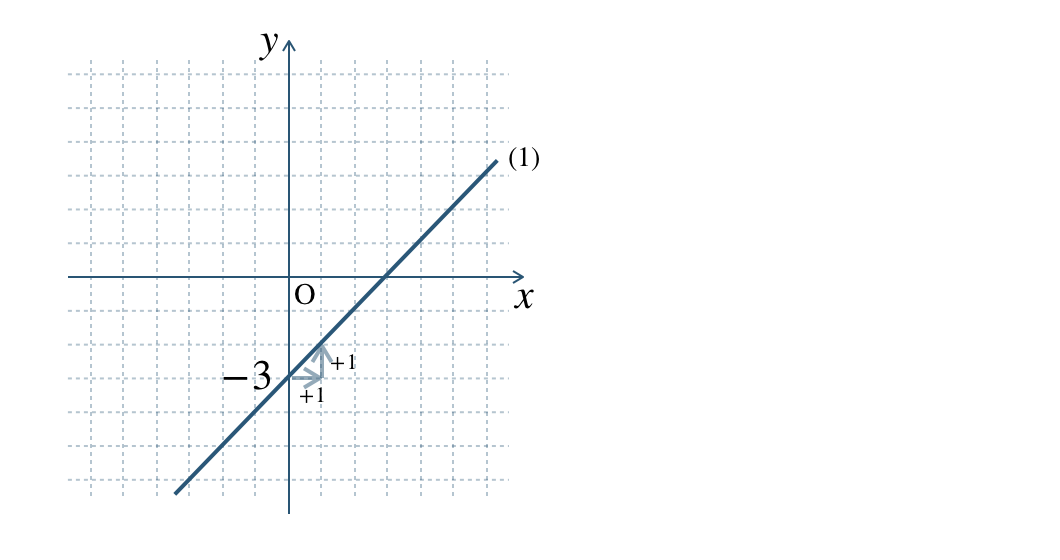
グラフより、
\(y\) 軸との交点 \((0~,~-3)\) で切片 \(-3\) となる
\(x\) の増加量 \(1\) 、 \(y\) の増加量 \(1\) で、傾き \(\begin{split}{\frac{\,1\,}{\,1\,}}=1\end{split}\)
したがって、
1次関数の式は \(\begin{split}y=x-3\end{split}\) となる
問題解説(2)
問題

次の図の (1) 〜 (4) の直線の式を求めよ。

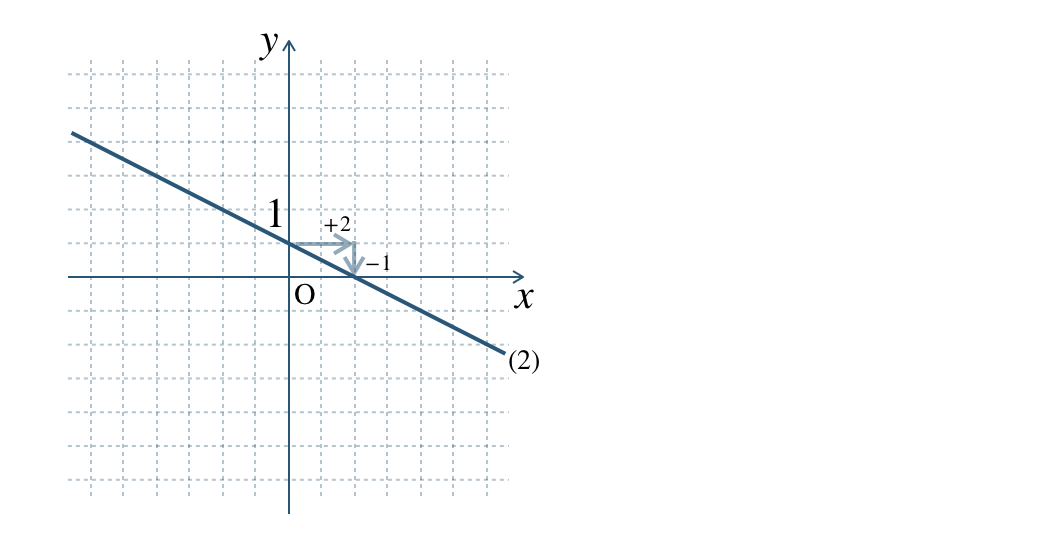
グラフより、
\(y\) 軸との交点 \((0~,~1)\) で切片 \(1\) となる
\(x\) の増加量 \(2\) 、 \(y\) の増加量 \(-1\) で、傾き \(\begin{split}-{\frac{\,1\,}{\,2\,}}\end{split}\)
※ \(x\) の増加量 \(-2\)、\(y\) の増加量 \(1\) でもよい。
したがって、
1次関数の式は \(\begin{split}y=-\frac{\,1\,}{\,2\,}x+1\end{split}\) となる
問題解説(3)
問題

次の図の (1) 〜 (4) の直線の式を求めよ。

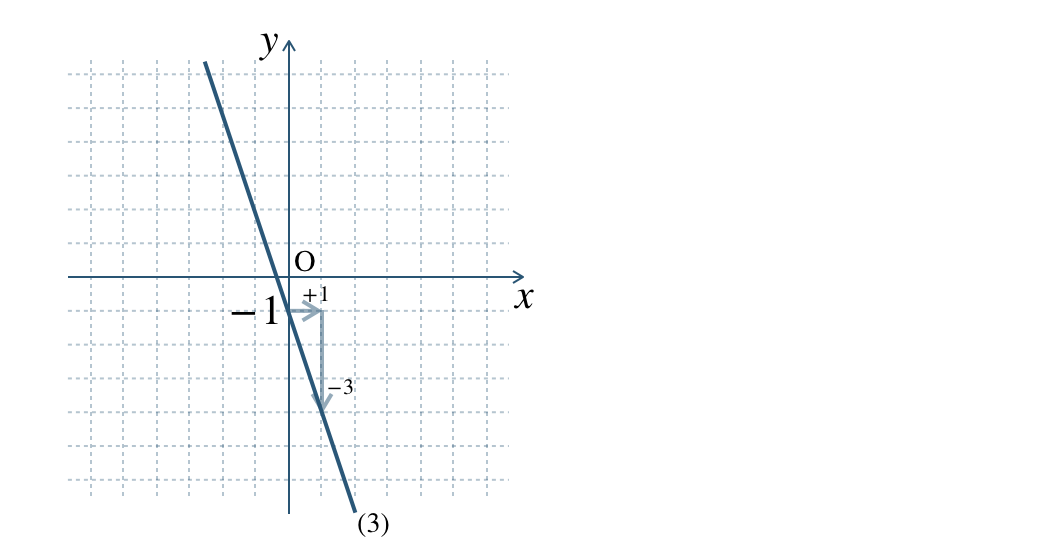
グラフより、
\(y\) 軸との交点 \((0~,~-1)\) で切片 \(-1\) となる
\(x\) の増加量 \(1\) 、 \(y\) の増加量 \(-3\) で、傾き \(\begin{split}-3\end{split}\)
※ \(x\) の増加量 \(-1\)、\(y\) の増加量 \(3\) でもよい。
したがって、
1次関数の式は \(\begin{split}y=-3x-1\end{split}\) となる
問題解説(4)
問題

次の図の (1) 〜 (4) の直線の式を求めよ。

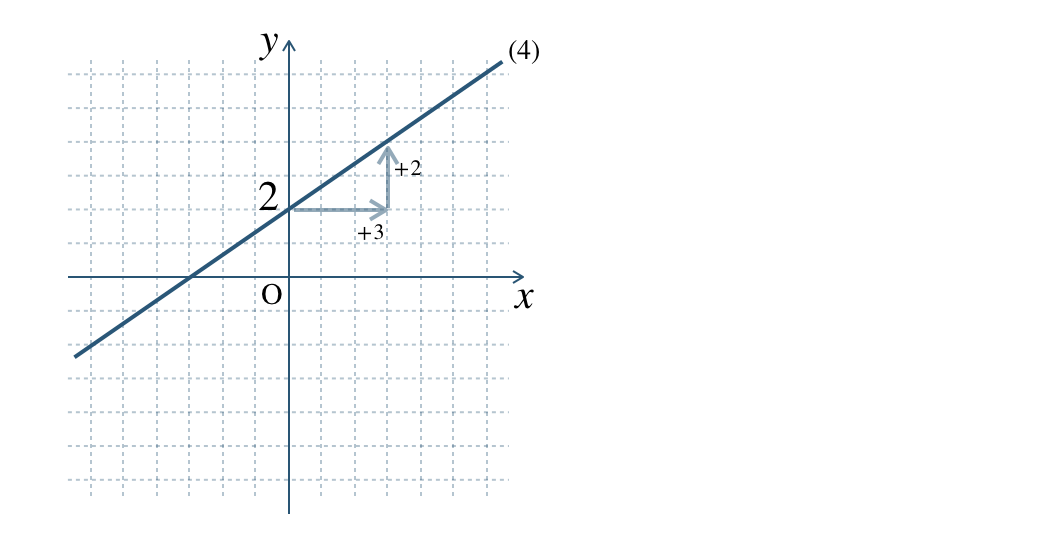
グラフより、
\(y\) 軸との交点 \((0~,~2)\) で切片 \(2\) となる
\(x\) の増加量 \(3\) 、 \(y\) の増加量 \(2\) で、傾き \(\begin{split}{\frac{\,2\,}{\,3\,}}\end{split}\)
したがって、
1次関数の式は \(\begin{split}y=\frac{\,2\,}{\,3\,}x+2\end{split}\) となる

【問題一覧】中2|1次関数
このページは「中学数学2 1次関数」の問題一覧ページとなります。解説の見たい単元名がわからないときは...


