2元1次方程式のグラフの解法
Point:2元1次方程式のグラフ
① \(y\) について解いて、1次関数の式 \(y=ax+b\) の形にする。
\(\begin{eqnarray}~~~2x+y&=&3\\[2pt]~~~y&=&-2x+3\end{eqnarray}\)
② 切片と傾きを読みとり、グラフをかく。
傾き \(-2\)、切片 \(3\) の直線をかく
■ 軸に平行な直線
\({\small (1)}~x=1\) のグラフは、
点 \((1~,~0)\) を通り、\(y\) 軸に平行な直線
\({\small (2)}~y=-2\) のグラフは、
点 \((0~,~-2)\) を通り、\(x\) 軸に平行な直線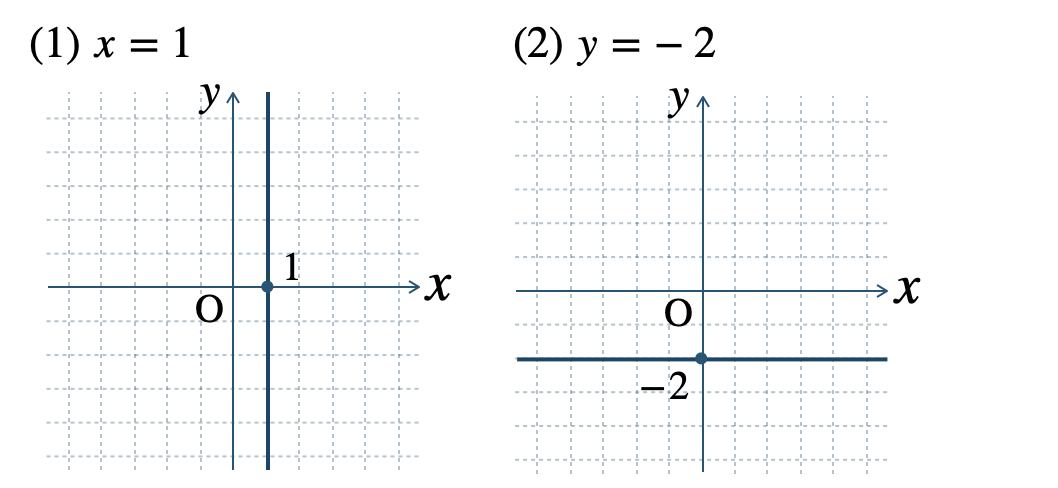
\(x\) と \(y\) の2つの文字についての1次方程式である
2元1次方程式 \(2x+y=3\) のグラフは、
① \(y\) について解いて、1次関数の式 \(y=ax+b\) の形にする。
\(\begin{eqnarray}~~~2x+y&=&3\\[2pt]~~~y&=&-2x+3\end{eqnarray}\)
② 切片と傾きを読みとり、グラフをかく。
傾き \(-2\)、切片 \(3\) の直線をかく
■ 軸に平行な直線
\({\small (1)}~x=1\) のグラフは、
点 \((1~,~0)\) を通り、\(y\) 軸に平行な直線
\({\small (2)}~y=-2\) のグラフは、
点 \((0~,~-2)\) を通り、\(x\) 軸に平行な直線

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:2元1次方程式のグラフ
問題解説(1)
問題
\(\begin{split}{\small (1)}~~3x+2y-6=0\end{split}\)
次の方程式のグラフをかけ。
\(\begin{split}{\small (1)}~~3x+2y-6=0\end{split}\)
\(y\) について解くと、
\(\begin{eqnarray}~~~3x+2y-6&=&0\\[2pt]~~~2y&=&-3x+6\end{eqnarray}\)
両辺を \(2\) で割ると、
\(\begin{eqnarray}\hspace{27pt}~~~\frac{\,2y\,}{\,2\,}&=&\frac{\,-3x\,}{\,2\,}+\frac{\,6\,}{\,2\,}\\[3pt]~~~y&=&-\frac{\,3\,}{\,2\,}x+3\end{eqnarray}\)
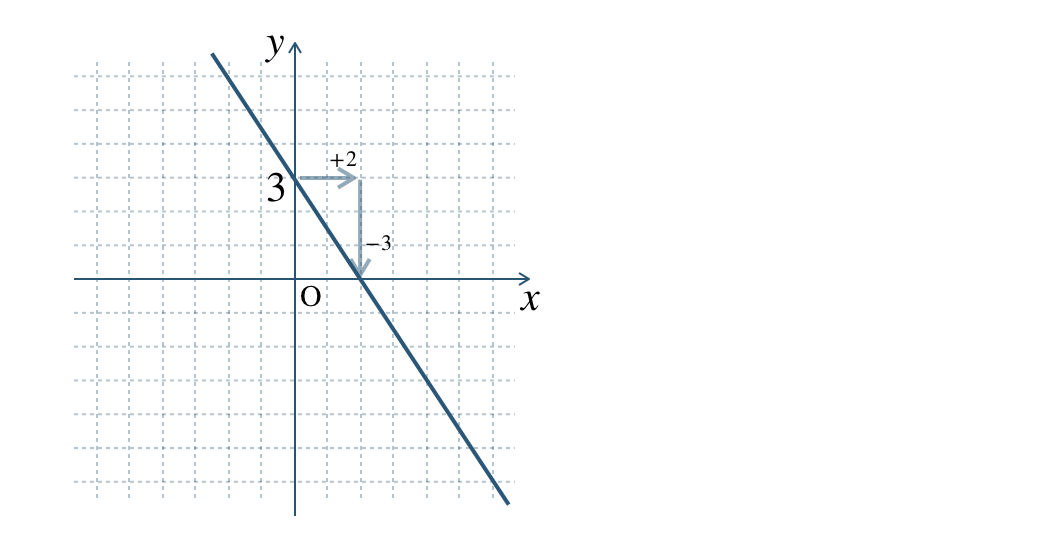
切片 \(3\) より、点 \((0~,~3)\) をとり、
傾き \(\begin{split}-{\frac{\,3\,}{\,2\,}}={\frac{\,-3\,}{\,2\,}}\end{split}\) より、
\(x\) の増加量 \(2\) のとき \(y\) の増加量 \(-3\) であるので、
問題解説(2)
問題
\(\begin{split}{\small (2)}~~\frac{\,1\,}{\,6\,}x-\frac{\,1\,}{\,3\,}y=1\end{split}\)
次の方程式のグラフをかけ。
\(\begin{split}{\small (2)}~~\frac{\,1\,}{\,6\,}x-\frac{\,1\,}{\,3\,}y=1\end{split}\)
\(y\) について解くと、
\(\begin{eqnarray}\hspace{12pt}~~~\frac{\,1\,}{\,6\,}x-\frac{\,1\,}{\,3\,}y&=&1\\[2pt]~~~-\frac{\,1\,}{\,3\,}y&=&-\frac{\,1\,}{\,6\,}x+1\end{eqnarray}\)
両辺を \(-3\) で掛け算すると、
\(\begin{eqnarray}~~~-\frac{\,1\,}{\,3\,}y{\, \small \times \,}(-3)&=&-\frac{\,1\,}{\,6\,}x{\, \small \times \,}(-3)+1{\, \small \times \,}(-3)\\[3pt]~~~y&=&\frac{\,1\,}{\,2\,}x-3\end{eqnarray}\)
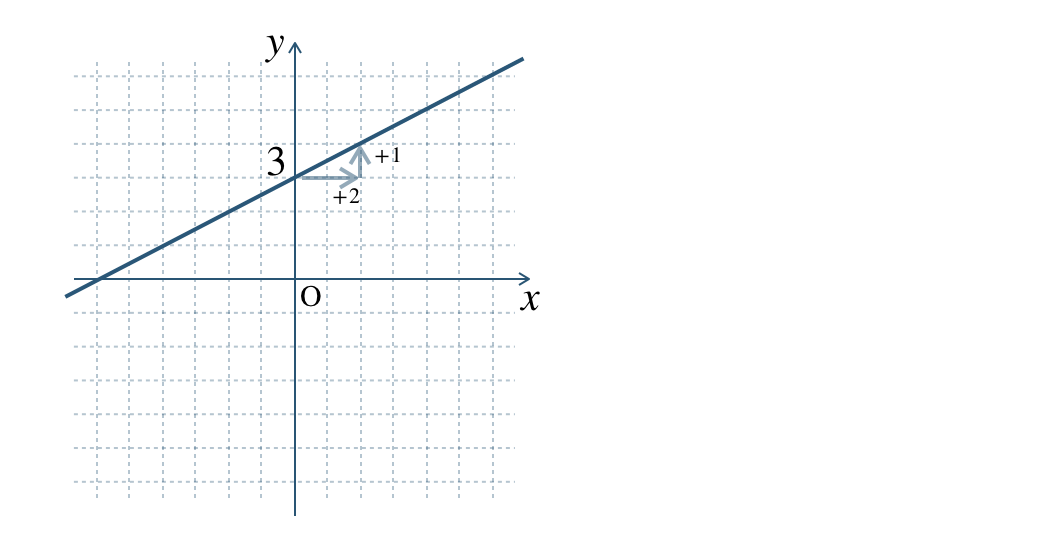
切片 \(-3\) より、点 \((0~,~-3)\) をとり、
傾き \(\begin{split}{\frac{\,1\,}{\,2\,}}\end{split}\) より、
\(x\) の増加量 \(2\) のとき \(y\) の増加量 \(1\) であるので、
問題解説(3)
問題
\(\begin{split}{\small (3)}~~3x=6\end{split}\)
次の方程式のグラフをかけ。
\(\begin{split}{\small (3)}~~3x=6\end{split}\)
\(x\) について解くと、
両辺を \(3\) で割ると、
\(\begin{eqnarray}~~~3x&=&6\\[3pt]~~~\frac{\,3x\,}{\,3\,}&=&\frac{\,6\,}{\,3\,}\\[3pt]~~~x&=&2\end{eqnarray}\)
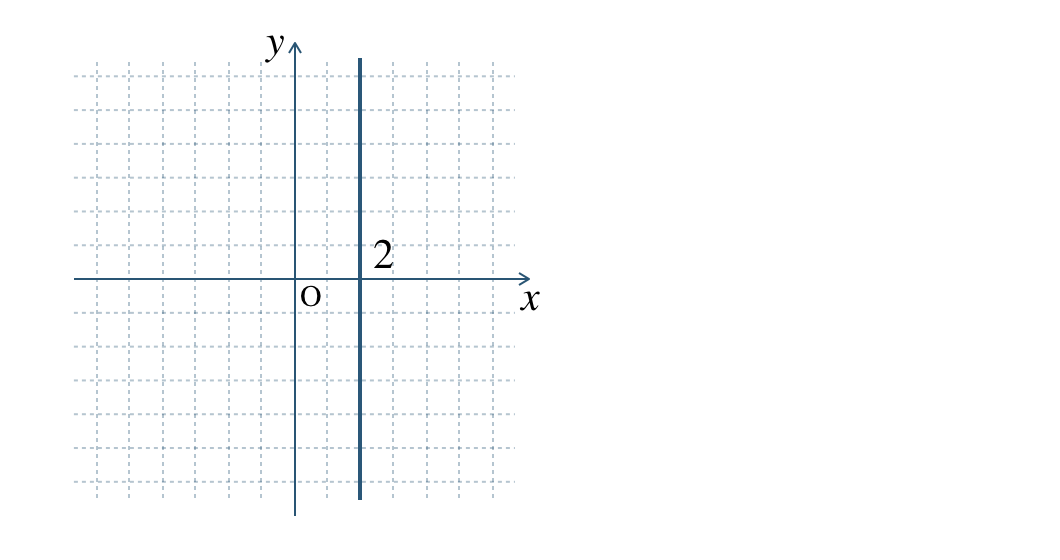
\(y\) がどんな値でも \(x=2\) となるので、
グラフは、点 \((2~,~0)\) を通り、\(y\) 軸に平行な直線となる
問題解説(4)
問題
\(\begin{split}{\small (4)}~~3y+12=0\end{split}\)
次の方程式のグラフをかけ。
\(\begin{split}{\small (4)}~~3y+12=0\end{split}\)
\(y\) について解くと、
( 両辺を \(3\) で割る )
\(\begin{eqnarray}~~~3y+12&=&0\\[2pt]~~~3y&=&-12\\[3pt]~~~\frac{\,3y\,}{\,3\,}&=&\frac{\,-12\,}{\,3\,}\\[3pt]~~~y&=&-4\end{eqnarray}\)
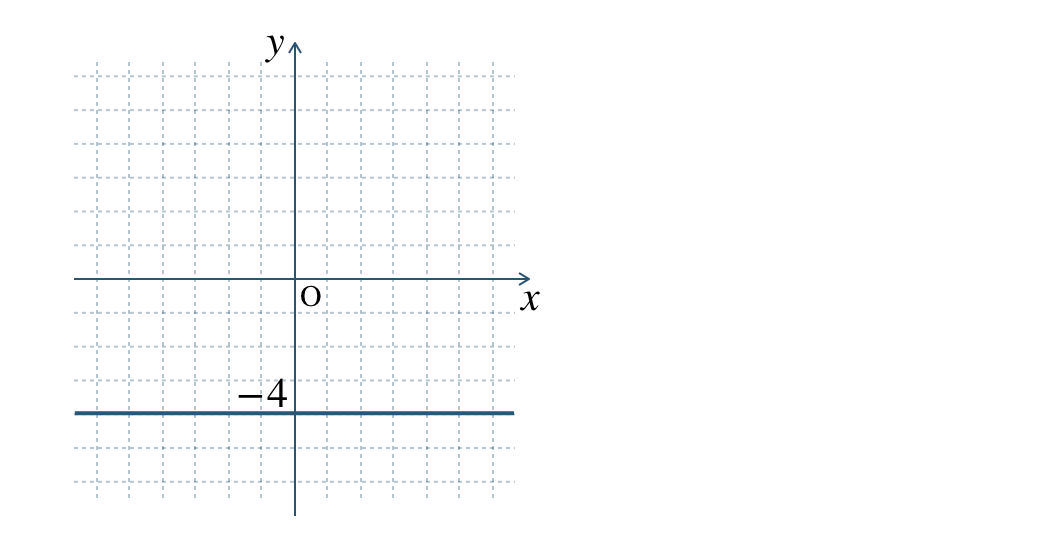
\(x\) がどんな値でも \(y=-4\) となるので、
グラフは、点 \((0~,~-4)\) を通り、\(x\) 軸に平行な直線となる

【問題一覧】中2|1次関数
このページは「中学数学2 1次関数」の問題一覧ページとなります。解説の見たい単元名がわからないときは...


