問題:1次関数と道のり
Aさんは家から学校までの道のり \(1400~{\rm m}\) を7時ちょうどに出発して歩いた。
次のグラフは、家を出発して \(x\) 分後の家からの道のりを \(y~{\rm m}\) として、\(x\) と \(y\) の関係を表したものである。
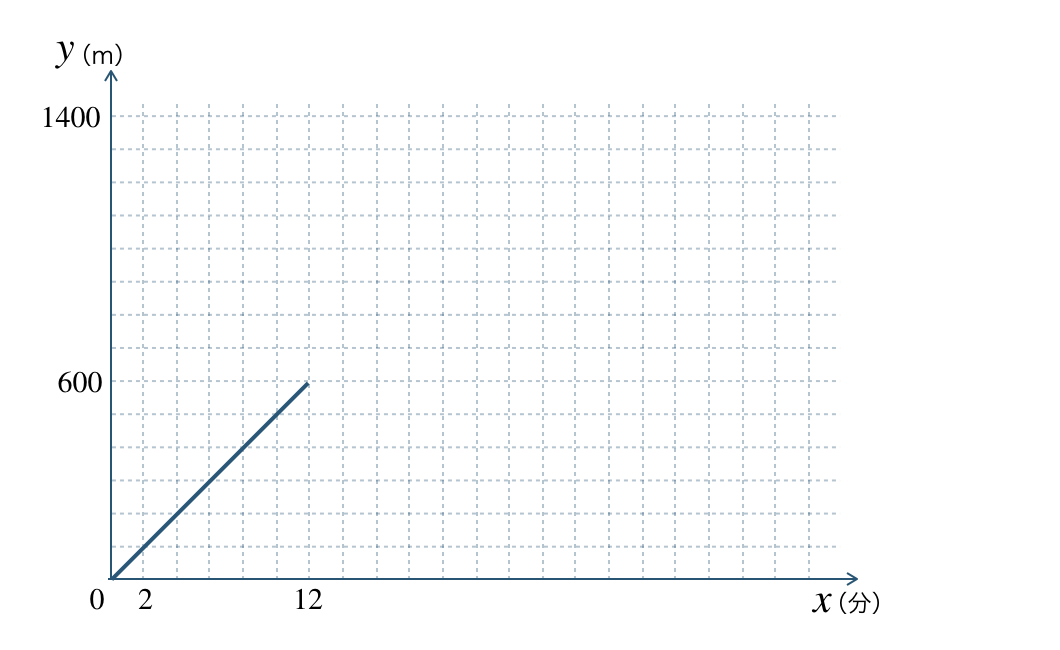
\({\small (1)}~\)Aさんは分速何 \({\rm m}\) で歩いたか答えよ。
\({\small (2)}~\)Aさんは家から \(600~{\rm m}\) の地点で \(10\) 分間休んだ後、学校まで同じ速さで歩いた。このことをグラフて表せ。
\({\small (3)}~\)Aさんが休んだ後、学校まで歩いた関係を \(y\) を \(x\) の式て表せ。
\({\small (4)}~\)Bさんは7時22分に家から学校まで分速 \(140~{\rm m}\) で走った。Bさんが家から学校まで走る \(x\) と \(y\) の関係をグラフで表し、\(y\) を \(x\) の式で表せ。
\({\small (5)}~\)BさんがAさんに追いつくのは7時何分何秒の家から何 \({\rm m}\) の地点か答えよ。
解法のPoint
\(x\) 軸を時間、\(y\) 軸を道のりとする1次関数のグラフの読み取り方は、

\({\small (1)}~\)速さ=直線の傾きとなる。
\(12-2=10\) 分で \(400~{\rm m}\) 進んでいるので、
\(\begin{split}400{\, \small \div \,}10=40\end{split}\) より、分速 \(40~{\rm m}\)
直線の傾きと等しくなる。
\({\small (2)}~\)グラフの直線の式は、
分速 \(40~{\rm m}\)=傾き \(40\) と点 \((2~,~0)\) より、
直線の式は、\(y=40x-80\)
\({\small (3)}~\)「追いつく」や「出会う」ときの時間と場所は、2直線の交点の座標より求める。
2直線の交点の \(x\) 座標=時間
2直線の交点の \(y\) 座標=道のり
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:1次関数と道のり
問題解説(1)
Aさんは家から学校までの道のり \(1400~{\rm m}\) を7時ちょうどに出発して歩いた。
次のグラフは、家を出発して \(x\) 分後の家からの道のりを \(y~{\rm m}\) として、\(x\) と \(y\) の関係を表したものである。

\({\small (1)}~\)Aさんは分速何 \({\rm m}\) で歩いたか答えよ。
グラフより、\(12\) 分で \(600~{\rm m}\) 進んでいるので、
\(\begin{split}~~~600{\, \small \div \,}12=50\end{split}\)
したがって、答えは 分速 \(50~{\rm m}\) となる
問題解説(2)
Aさんは家から学校までの道のり \(1400~{\rm m}\) を7時ちょうどに出発して歩いた。
次のグラフは、家を出発して \(x\) 分後の家からの道のりを \(y~{\rm m}\) として、\(x\) と \(y\) の関係を表したものである。

\({\small (2)}~\)Aさんは家から \(600~{\rm m}\) の地点で \(10\) 分間休んだ後、学校まで同じ速さで歩いた。このことをグラフて表せ。
7時12分から \(10\) 分間は \(600~{\rm m}\) の地点で動かない
また、7時22分からは分速 \(50~{\rm m}\) で
残りの \(1400-600=800~{\rm m}\) 歩くので、
時間=道のり÷速さより、
\(\begin{split}~~~800{\, \small \div \,}50=16
\end{split}\)
\(16\) 分後の7時38分に \(1400~{\rm m}\) 地点にいる
よって、2点 \((22~,~600)~,~(38~,~1400)\) を通る直線を結ぶと、
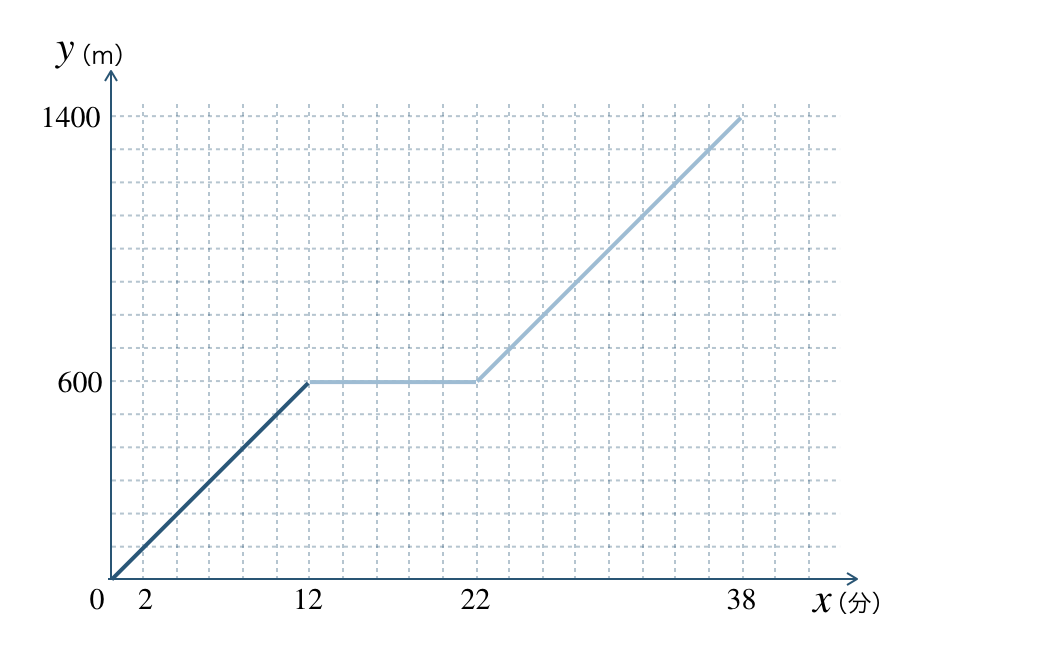
問題解説(3)
Aさんは家から学校までの道のり \(1400~{\rm m}\) を7時ちょうどに出発して歩いた。
次のグラフは、家を出発して \(x\) 分後の家からの道のりを \(y~{\rm m}\) として、\(x\) と \(y\) の関係を表したものである。

\({\small (3)}~\)Aさんが休んだ後、学校まで歩いた関係を \(y\) を \(x\) の式て表せ。
速さ=直線の傾きとなる
分速 \(50~{\rm m}\) であるので直線の式は、
\(\begin{split}~~~y=50x+b\end{split}\)
点 \((22~,~600)\) を通るので、\(x=22~,~y=600\) を代入すると、
(※ 点 \((38~,~1400)\) でもよい。)
\(\begin{eqnarray}~~~600&=&50{\, \small \times \,}22+b\\[2pt]~~~600&=&1100+b\\[2pt]~~~-b&=&1100-600\\[2pt]~~~-b&=&500\\[2pt]~~~b&=&-500\end{eqnarray}\)
したがって、直線の式は \(\begin{split}y=50x-500\end{split}\) となる
問題解説(4)
Aさんは家から学校までの道のり \(1400~{\rm m}\) を7時ちょうどに出発して歩いた。
次のグラフは、家を出発して \(x\) 分後の家からの道のりを \(y~{\rm m}\) として、\(x\) と \(y\) の関係を表したものである。

\({\small (4)}~\)Bさんは7時22分に家から学校まで分速 \(140~{\rm m}\) で走った。
Bさんが家から学校まで走る \(x\) と \(y\) の関係をグラフで表し、\(y\) を \(x\) の式て表せ。
Bさんは7時22分に家から分速 \(140~{\rm m}\) で走っているので、\(1400~{\rm m}\) 先の学校までに進む時間は、
時間=道のり÷速さより、
\(\begin{split}~~~1400{\, \small \div \,}140=10\end{split}\)
これより、\(10\) 分かかり7時32分に学校に着く
よって、2点 \((22~,~0)~,~(32~,~1400)\) を通る直線を結ぶと、
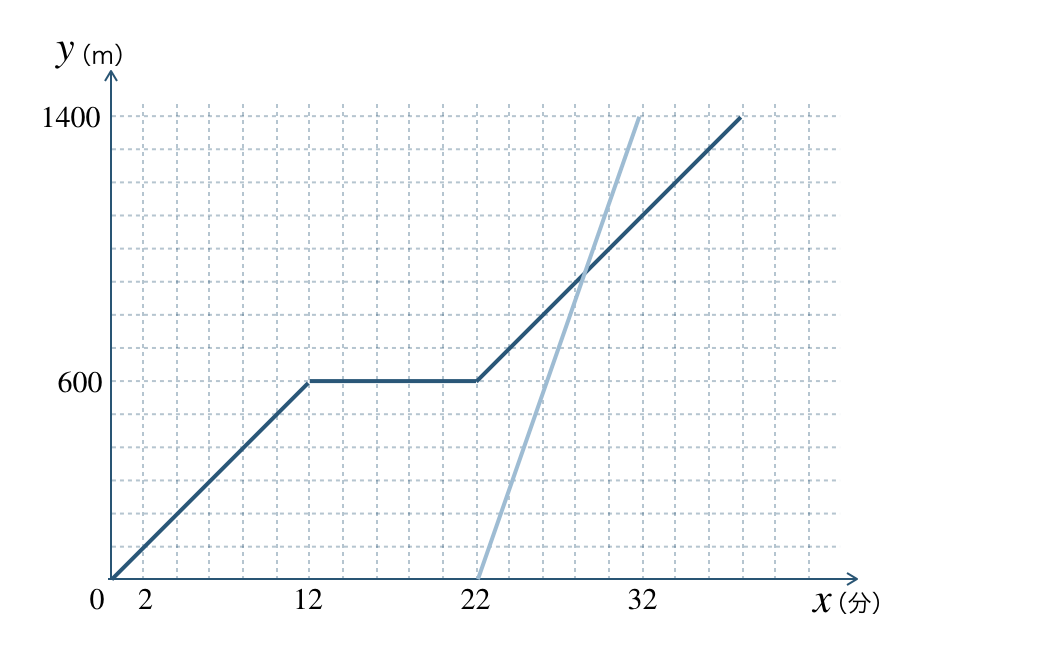
また、直線の式は傾きが分速 \(140~{\rm m}\) となるので、
\(\begin{split}~~~y=140x+c\end{split}\)
点 \((22~,~0)\) を通るので、\(x=22~,~y=0\) を代入すると、
(※ 点 \((32~,~1400)\) でもよい。)
\(\begin{eqnarray}~~~0&=&140{\, \small \times \,}22+c\\[2pt]~~~-c&=&3080\\[2pt]~~~c&=&-3080\end{eqnarray}\)
したがって、直線の式は \(\begin{split}y=140x-3080\end{split}\) となる
問題解説(5)
Aさんは家から学校までの道のり \(1400~{\rm m}\) を7時ちょうどに出発して歩いた。
次のグラフは、家を出発して \(x\) 分後の家からの道のりを \(y~{\rm m}\) として、\(x\) と \(y\) の関係を表したものである。

\({\small (5)}~\)BさんがAさんに追いつくのは7時何分何秒の家から何 \({\rm m}\) の地点か答えよ。
BさんがAさんに追いつくのは、クラブが交わるとき、
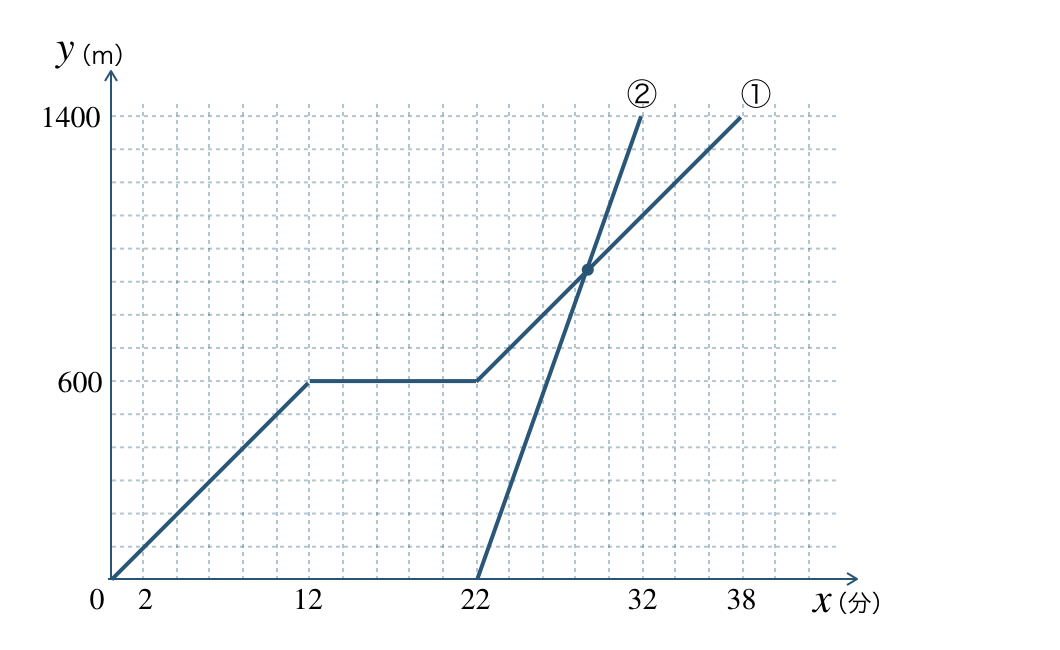
\(22≦x≦32\) でのAさん、Bさんのそれぞれの直線の式を連立すると、
\(~~~\begin{eqnarray} \left\{\begin{array}{l}y=50x-500 ~&\cdots{\large ①}\\y=140x-3080 ~&\cdots{\large ②}\end{array}\right.\end{eqnarray}\)
②を①に代入すると、
\(\begin{eqnarray}~~~140x-3080&=&50x-500\\[2pt]~~~140x-50x&=&-500+3080\\[3pt]~~~90x&=&2580\\[3pt]~~~\frac{\,90x\,}{\,90\,}&=&\frac{\,2580\,}{\,90\,}\\[3pt]~~~x&=&\frac{\,86\,}{\,3\,}\end{eqnarray}\)
①に代入すると、
\(\begin{eqnarray}~~~y&=&50{\, \small \times \,}\frac{\,86\,}{\,3\,}-500\\[3pt]~~~&=&\frac{\,4300-1500\,}{\,3\,}\\[3pt]~~~&=&\frac{\,2800\,}{\,3\,}\end{eqnarray}\)
また、\(\begin{split}{\frac{\,86\,}{\,3\,}}\end{split}\) 分は、
\(\begin{split}~~~\frac{\,86\,}{\,3\,}=28+\frac{\,2\,}{\,3\,}\end{split}\)
\(\begin{split}{\frac{\,2\,}{\,3\,}}\end{split}\) 分を秒にすると、
\(\begin{split}~~~\frac{\,2\,}{\,3\,}{\, \small \times \,}60=2{\, \small \times \,}20=40\end{split}\)
これより、28分40秒となる
したがって、答えは
7時28分40秒、家から \(\begin{split}{\frac{\,2800\,}{\,3\,}}~{\rm m}\end{split}\) の地点
となる



