今回の問題は「図形の性質と証明」です。
\(~\)数研出版 これからの数学2 p.134 問3~4
\(~\)東京書籍 新しい数学2 p.119~121
\(~\)啓林館 未来へひろがる数学2 p.117~119
問題
\({\small (1)}~\)次の図において、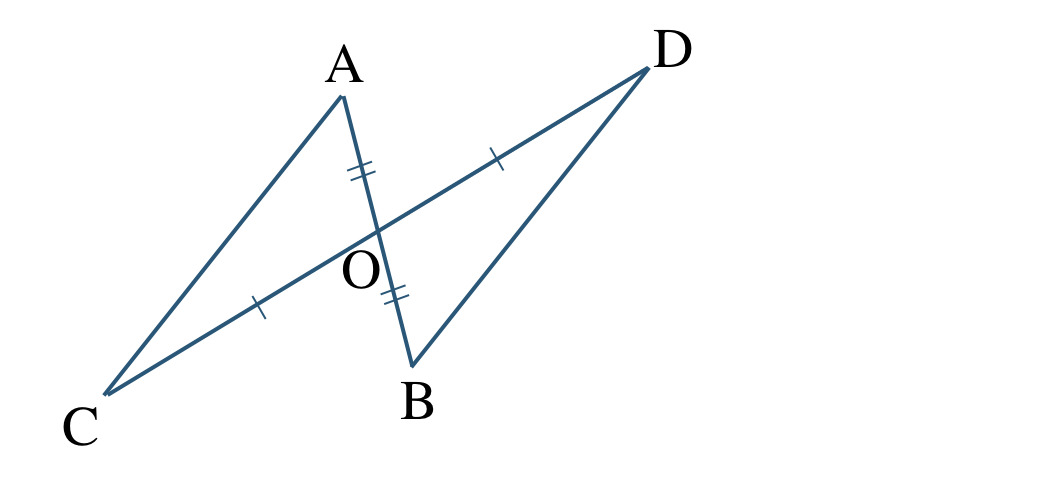
\({\small (2)}~\)次の図において、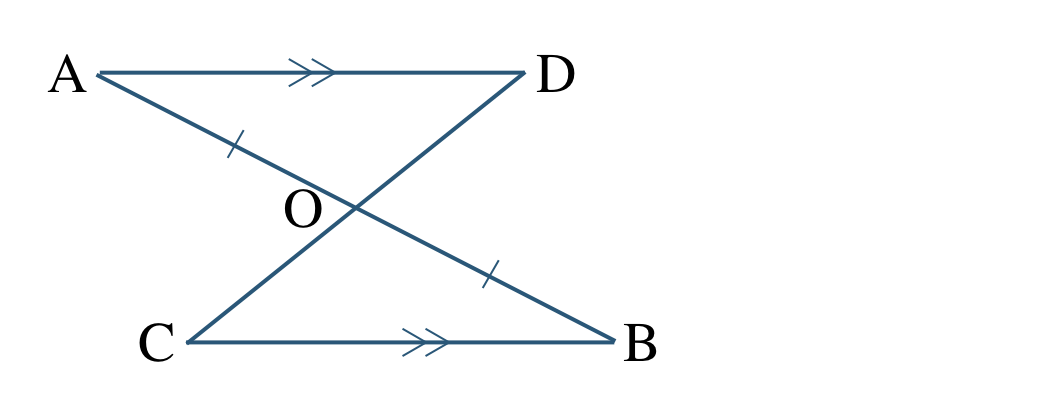
\({\small (3)}~\)角の二等分線の作図において、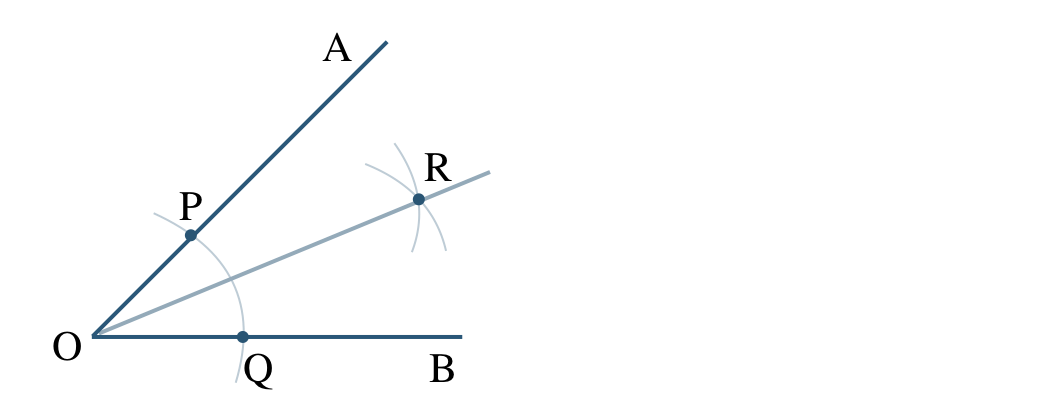
次の証明をせよ。
\({\small (1)}~\)次の図において、
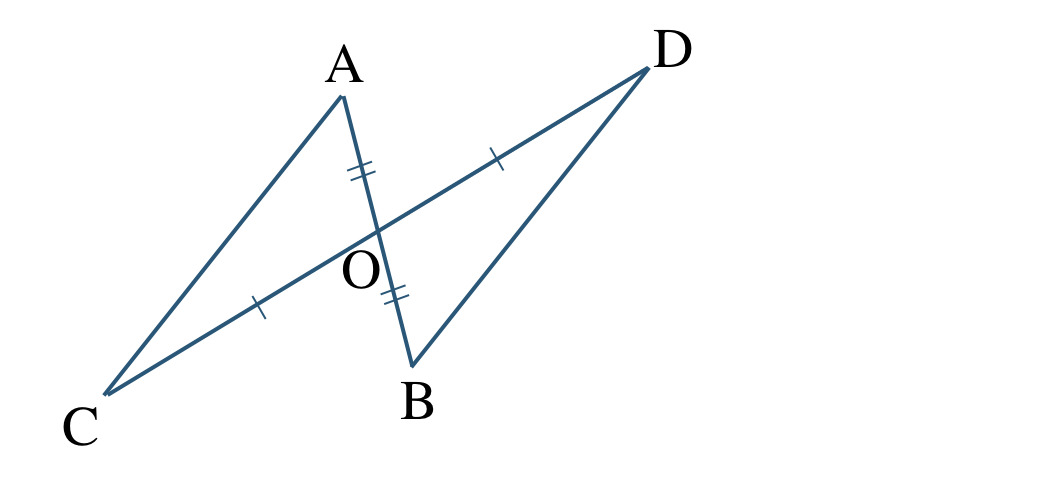
\({\rm AO=BO~,~CO=DO}\) ならば \({\rm AC\,//\,DB}\)
\({\small (2)}~\)次の図において、

\({\rm AO=BO~,~AD\,//\,CB}\) ならば \({\rm AD=CB}\)
\({\small (3)}~\)角の二等分線の作図において、

半直線 \({\rm OR}\) が \(\angle {\rm AOB}\) を二等分する
Point:図形の性質と証明
証明を書き始める前に、見通しをたてる。
・結論を導くために、示すべき合同な2つの三角形を見つける。
・仮定や仮定から導かれる根拠となることがらを考える。
・根拠より、合同条件を考える。
・三角形の合同から結論を導く。
■ 証明のすすめ方
① 着目している三角形がどれとどれかを書く。
② 仮定から根拠となることがらを書く。
③ 仮定から導かられる根拠を書く。
④ 根拠から三角形の合同条件を書く。
⑤ 三角形が合同であることを記号 \(\equiv\) で表す。
⑥ 合同な図形の性質より、結論を導く。
図形の性質の証明方法は、
証明を書き始める前に、見通しをたてる。
・結論を導くために、示すべき合同な2つの三角形を見つける。
・仮定や仮定から導かれる根拠となることがらを考える。
・根拠より、合同条件を考える。
・三角形の合同から結論を導く。
■ 証明のすすめ方
① 着目している三角形がどれとどれかを書く。
② 仮定から根拠となることがらを書く。
③ 仮定から導かられる根拠を書く。
④ 根拠から三角形の合同条件を書く。
⑤ 三角形が合同であることを記号 \(\equiv\) で表す。
⑥ 合同な図形の性質より、結論を導く。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
次のページ「解法のPointと問題解説」


