問題:二等辺三角形の性質
次の問いに答えよ。
\({\small (1)}~\)次の \({\rm AB=AC}\) 二等辺三角形 \({\rm ABC}\) について、
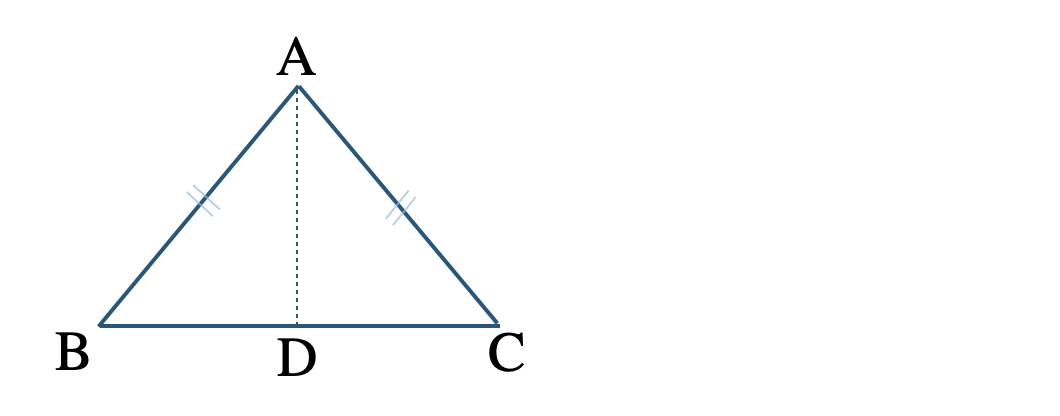
① 二等辺三角形の定義を答えよ。
② \(\angle {\rm A}\) を何というか答えよ。
③ 辺 \({\rm BC}\) を何というか答えよ。
④ \(\angle {\rm B}~,~\angle {\rm C}\) を何というか答えよ。また、\(\angle {\rm B}\) と \(\angle {\rm C}\) の関係を答えよ。
⑤ \(\angle {\rm A}\) の二等分線と辺 \({\rm BC}\) との交点を \({\rm D}\) とするとき、二等分線 \({\rm AD}\) と辺 \({\rm BC}\) の関係、線分 \({\rm BD}\) と \({\rm CD}\) の関係をそれぞれ答えよ。
\({\small (2)}~\)次の \(\triangle {\rm ABC}\) が \({\rm AB=AC}\) の二等辺三角形であるとき、\(\angle x~,~\angle y\) の大きさを求めよ。
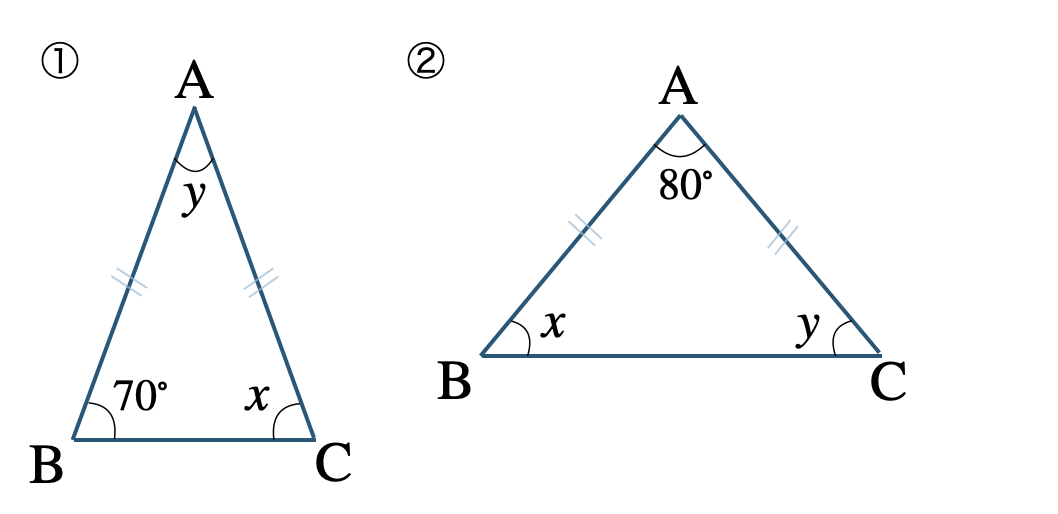
解法のPoint
■ 二等辺三角形
【定義】2つの辺が等しい三角形を二等辺三角形という。
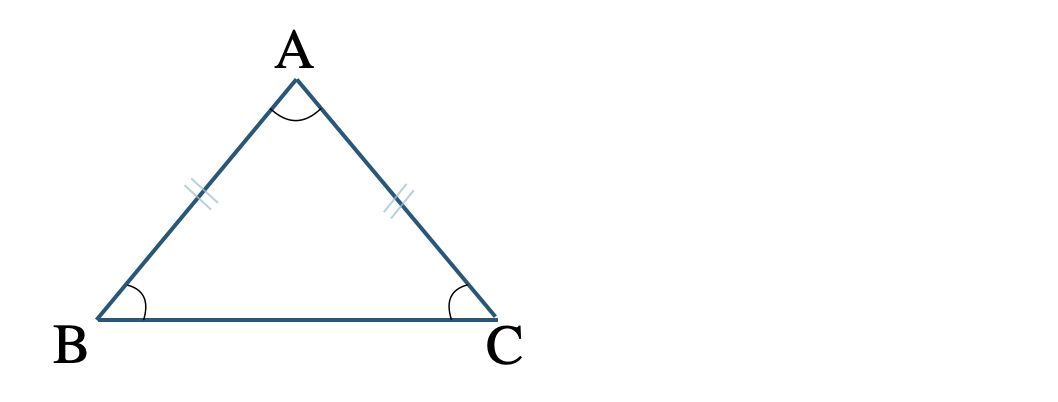
\(\triangle {\rm ABC}\) が \({\rm AB=AC}\) の二等辺三角形であるとき、
等しい辺のつくる角 \(\angle {\rm A}\) を「頂角」
頂角に対する辺 \({\rm BC}\) を「底辺」
底辺の両端の角 \(\angle{\rm B}~,~ \angle{\rm C}\) を「底角」
■ 定義と定理
使うことば(用語や記号)の意味をはっきり述べたものを「定義」という。
また、定義から証明されたことがらのうち、基本となるもの(よく使う大事なもの)を「定理」という。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
\(\triangle {\rm ABC}\) が \({\rm AB=AC}\) の二等辺三角形であるとき、
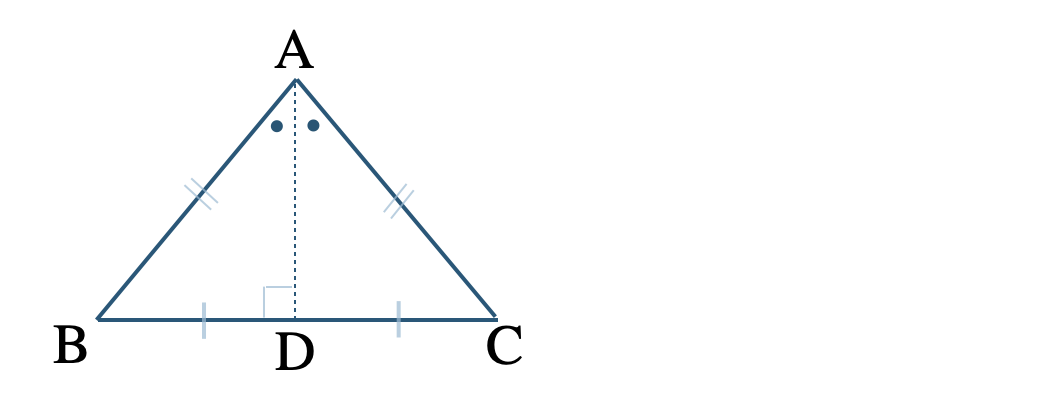
【定理】二等辺三角形の底角が等しい。
上の図で、\(\angle{\rm B}=\angle{\rm C}\)
【定理】二等辺三角形の頂角の二等分線は、底角を垂直に二等分する。
上の図で、\({\rm AD\perp BC~,~BD=CD}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:二等辺三角形の性質
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)次の \({\rm AB=AC}\) 二等辺三角形 \({\rm ABC}\) について、

① 二等辺三角形の定義を答えよ。
② \(\angle {\rm A}\) を何というか答えよ。
③ 辺 \({\rm BC}\) を何というか答えよ。
④ \(\angle {\rm B}~,~\angle {\rm C}\) を何というか答えよ。また、\(\angle {\rm B}\) と \(\angle {\rm C}\) の関係を答えよ。
⑤ \(\angle {\rm A}\) の二等分線と辺 \({\rm BC}\) との交点を \({\rm D}\) とするとき、二等分線 \({\rm AD}\) と辺 \({\rm BC}\) の関係、線分 \({\rm BD}\) と \({\rm CD}\) の関係をそれぞれ答えよ。
① 定義は、
2つの辺が等しい三角形を二等辺三角形
② 等しい辺のつくる角であるので、
\(\angle {\rm A}\) は頂角 という
③ 頂角 \(\angle {\rm A}\) に対する辺であるので、
辺 \({\rm BC}\) は底辺 という
④ 底辺 \({\rm BC}\) の両端の角があるので、
\(\angle {\rm B}~,~\angle {\rm C}\) は底角 という
また、二等辺三角形の定理より、2つの底角が等しいので、
\(\angle {\rm B}=\angle {\rm C}\) となる
⑤ 二等辺三角形の定理より、頂角の二等分線は底辺を垂直に二等分するので、
\({\rm AD\perp BC~,~BD=CD}\) となる
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)次の \(\triangle {\rm ABC}\) が \({\rm AB=AC}\) の二等辺三角形であるとき、\(\angle x~,~\angle y\) の大きさを求めよ。

① 二等辺三角形の底角が等しいので、
\(~~~\angle x=70^\circ\)
三角形な内角の和が \(180^\circ\) より、
\(\begin{eqnarray}~~~\angle y+70^\circ+70^\circ&=&180^\circ\\[2pt]~~~\angle y&=&180^\circ-(70^\circ+70^\circ)\\[2pt]~~~\angle y&=&180^\circ-140^\circ\\[2pt]~~~\angle y&=&40^\circ\end{eqnarray}\)
したがって、\(\angle x=70^\circ~,~\angle y=40^\circ\) となる
② 三角形の内角の和が \(180^\circ\) より、
\(\begin{eqnarray}~~~80^\circ+\angle x+\angle y&=&180^\circ\\[2pt]~~~\angle x+\angle y&=&180^\circ-80^\circ\\[2pt]~~~\angle x+\angle y&=&100^\circ\end{eqnarray}\)
また、二等辺三角形の底角が等しいより、\(\angle x=\angle y\) となるので、
\(\begin{eqnarray}~~~\angle x+\angle x&=&100^\circ\\[2pt]~~~2\angle x&=&100^\circ\\[3pt]~~~\angle x&=&50^\circ\end{eqnarray}\)
また、\(\angle x=\angle y\) となるので、
\(~~~\angle y=50^\circ\)
したがって、\(\angle x=50^\circ~,~\angle y=50^\circ\) となる



