問題:ことがらの逆と反例
次のことがらの逆を答えよ。また、それが正しいかどうかを調べて正しくない場合は反例も答えよ。
\({\small (1)}~\)\(\triangle {\rm ABC}\) で、
\({\rm AB=AC}\) ならば \(\angle{\rm B}=\angle{\rm C}\)
\({\small (2)}~\)整数 \(a~,~b\) で、\(a\) も \(b\) も奇数 ならば \(a+b\) は偶数。
\({\small (3)}~\)\(\triangle {\rm ABC}\) で、
\(\angle{\rm A}\) が直角 ならば \(\angle{\rm B}+\angle{\rm C}=90^\circ\)
\({\small (4)}~\)2直線が平行 ならば 錯角が等しい。
\({\small (5)}~\)2つの三角形が合同 ならば その2つの三角形の面積が等しい。
\({\small (6)}~\)\(x\) が \(6\) の倍数 ならば \(x\) は \(2\) の倍数。
\({\small (7)}~\)整数 \(a~,~b\) で、\(a\) が奇数で \(b\) が偶数 ならば \(ab\) は偶数。
\({\small (8)}~\)\(\triangle {\rm ABC}\) と \(\triangle {\rm A^{\prime}B^{\prime}C^{\prime}}\) において、
\(\triangle {\rm ABC}\equiv\triangle {\rm A^{\prime}B^{\prime}C^{\prime}}\) ならば \({\rm AB=A^{\prime}B^{\prime}}\)
追加の練習問題のページはこちら→
ことがらの逆と反例|練習問題50問
解法のPoint
ことがら「◯◯ならば、◇◇である」の逆は、
仮定と結論を入れかえて、
「◇◇ならば、◯◯である」となる。
■ ことがらの反例
あることがらの仮定が成り立つが、結論が成り立たない例を「反例」という。
※ あることがらが正しい場合でも、そのことがらの逆が正しいとは限らない。
ことがら「 \(x>7\) ならば \(x{\small ~≧~}2\) 」の逆は、
「 \(x{\small ~≧~}2\) ならば \(x>7\) 」
これは反例の \(x=3\) などがあり、正しくない。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:ことがらの逆と反例
問題解説(1)
次のことがらの逆を答えよ。また、それが正しいかどうかを調べて正しくない場合は反例も答えよ。
\({\small (1)}~\)\(\triangle {\rm ABC}\) で、
\({\rm AB=AC}\) ならば \(\angle{\rm B}=\angle{\rm C}\)
このことがらの逆は、
\(\triangle {\rm ABC}\) で、
\(\angle{\rm B}=\angle{\rm C}\) ならば \({\rm AB=AC}\)
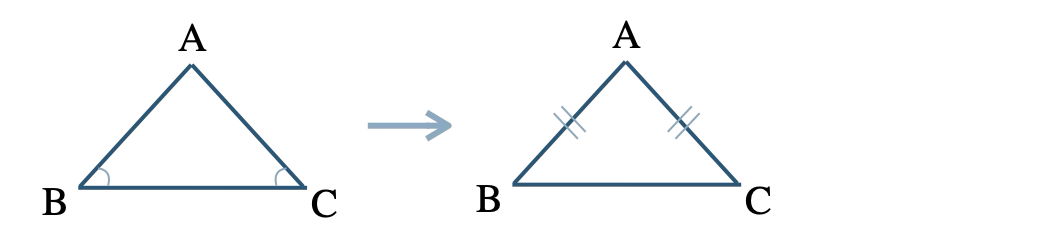
二等辺三角形の定理より、底角が等しいならばその三角形は二等辺三角形となる
したがって、正しい
問題解説(2)
次のことがらの逆を答えよ。また、それが正しいかどうかを調べて正しくない場合は反例も答えよ。
\({\small (2)}~\)整数 \(a~,~b\) で、\(a\) も \(b\) も奇数 ならば \(a+b\) は偶数。
このことがらの逆は、
\(a+b\) が偶数 ならば \(a\) も \(b\) も奇数
\(a=2~,~b=4\) のとき、\(a+b=6\) となり偶数だが \(a\) も \(b\) も偶数となる
よって、正しくない
また、反例は \(a=2~,~b=4\)
(※ 他に \(a=8~,~b=6\) など)
問題解説(3)
次のことがらの逆を答えよ。また、それが正しいかどうかを調べて正しくない場合は反例も答えよ。
\({\small (3)}~\)\(\triangle {\rm ABC}\) で、
\(\angle{\rm A}\) が直角 ならば \(\angle{\rm B}+\angle{\rm C}=90^\circ\)
このことがらの逆は、
\(\triangle {\rm ABC}\) で、
\(\angle{\rm B}+\angle{\rm C}=90^\circ\) ならば \(\angle{\rm A}\) が直角
三角形の内角の和が \(180^\circ\) より、
\(~~~\angle {\rm A}=180^\circ-(\angle {\rm B}+\angle {\rm C})=90^\circ\)
よって、正しい
問題解説(4)
次のことがらの逆を答えよ。また、それが正しいかどうかを調べて正しくない場合は反例も答えよ。
\({\small (4)}~\)2直線が平行 ならば 錯角が等しい。
このことがらの逆は、
錯角が等しい ならば 2直線が平行
平行線と錯角の定理の逆より、錯角が等しいならば2直線が平行となる
したがって、正しい
問題解説(5)
次のことがらの逆を答えよ。また、それが正しいかどうかを調べて正しくない場合は反例も答えよ。
\({\small (5)}~\)2つの三角形が合同 ならば その2つの三角形の面積が等しい。
このことがらの逆は、
2つの三角形の面積が等しい ならば 2つの三角形が合同
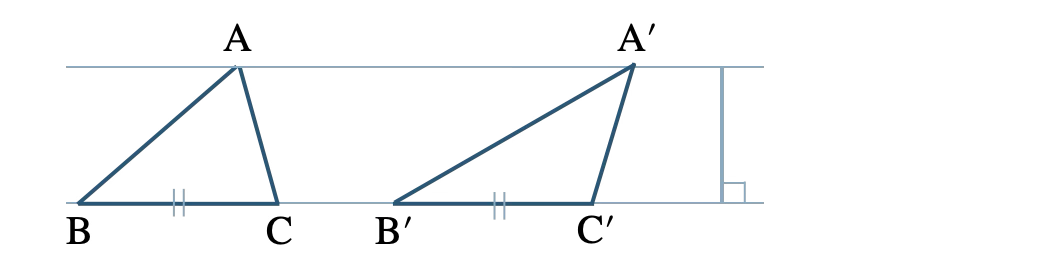
面積が等しい三角形でも合同にならない場合でもある
よって、正しくない
反例は、次の図のようになる
問題解説(6)
次のことがらの逆を答えよ。また、それが正しいかどうかを調べて正しくない場合は反例も答えよ。
\({\small (6)}~\)\(x\) が \(6\) の倍数 ならば \(x\) は \(2\) の倍数。
このことがらの逆は、
\(x\) が \(2\) の倍数 ならば \(x\) は \(6\) の倍数
\(x=4\) のとき、\(2\) の倍数であるが \(6\) の倍数でない
よって、正しくない
反例は、\(x=4\)
(※ \(x=2~,~8~,~10~,~\cdots\) など)
問題解説(7)
次のことがらの逆を答えよ。また、それが正しいかどうかを調べて正しくない場合は反例も答えよ。
\({\small (7)}~\)整数 \(a~,~b\) で、\(a\) が奇数で \(b\) が偶数 ならば \(ab\) は偶数。
このことがらの逆は、
\(ab\) が偶数 ならば \(a\) が奇数で \(b\) が偶数
\(a=2~,~b=3\) のとき、\(ab=6\) となり偶数で \(a\) が偶数で \(b\) が奇数となる
よって、正しくない
反例は、\(a=2~,~b=3\)
(※ \(a=2~,~b=4\) なども)
問題解説(8)
次のことがらの逆を答えよ。また、それが正しいかどうかを調べて正しくない場合は反例も答えよ。
\({\small (8)}~\)\(\triangle {\rm ABC}\) と \(\triangle {\rm A^{\prime}B^{\prime}C^{\prime}}\) において、
\(\triangle {\rm ABC}\equiv\triangle {\rm A^{\prime}B^{\prime}C^{\prime}}\) ならば \({\rm AB=A^{\prime}B^{\prime}}\)
このことがらの逆は、
\(\triangle {\rm ABC}\) と \(\triangle {\rm A^{\prime}B^{\prime}C^{\prime}}\) において、
\({\rm AB=A^{\prime}B^{\prime}}\) ならば \(\triangle {\rm ABC}\equiv\triangle {\rm A^{\prime}B^{\prime}C^{\prime}}\)
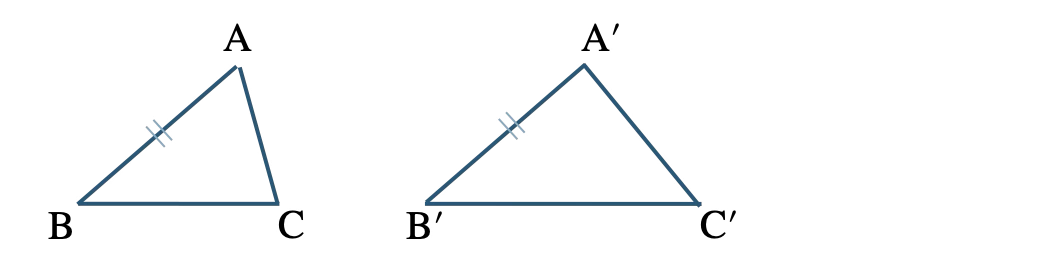
三角形の合同条件より、1組の辺が等しい場合は合同とはいえない
よって、正しくない
反例は、次の図のようになる
追加の練習問題のページはこちら→
ことがらの逆と反例|練習問題50問



