辺や角の条件と平行四辺形

Point：辺や角の条件と平行四辺形

四角形 \({\rm ABCD}\) の辺や角の条件より、この四角形が平行四辺形になるか調べる方法は、

---

① 四角形 \({\rm ABCD}\) の図をかき、条件を書きこむ。

---

② 「平行四辺形になるための条件」のうち当てはまるものがあるかを調べる。

---

　\({\small (1)}~\)２組の対辺がそれぞれ平行である(定義)
　\({\small (2)}~\)２組の対辺がそれぞれ等しい(定理)
　\({\small (3)}~\)２組の対角がそれぞれ等しい(定理)
　\({\small (4)}~\)対角線がそれぞれの中点で交わる(定理)
　\({\small (5)}~\)１組の対辺が等しくて平行である(定理)

---

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

問題

次の四角形 \({\rm ABCD}\) が平行四辺形であるか調べよ。

---

\({\small (1)}~\)\(\angle{\rm A}=\angle{\rm B}~,~\angle{\rm C}=\angle{\rm D}\)

四角形 \({\rm ABCD}\) に条件を書きこむと、

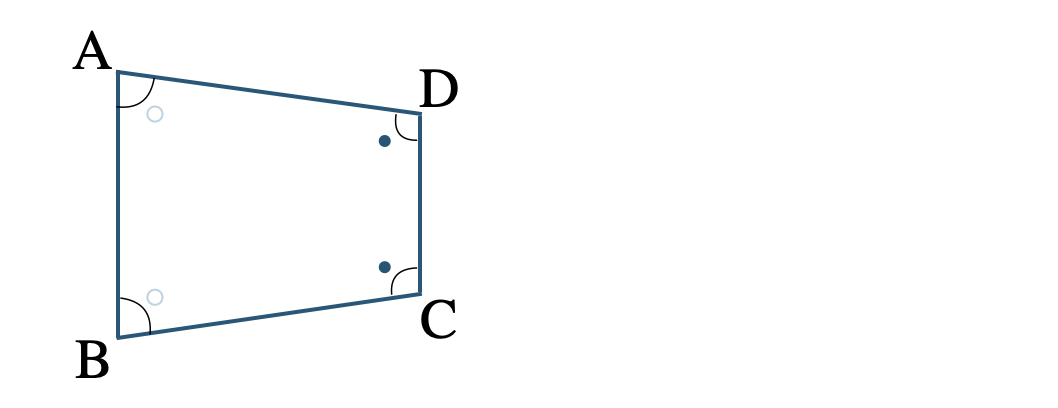
これより、平行四辺形になるための条件にあてはまるものはない
したがって、
四角形 \({\rm ABCD}\) は平行四辺形でない

問題

次の四角形 \({\rm ABCD}\) が平行四辺形であるか調べよ。

---

\({\small (2)}~\)\({\rm AB=CD~,~AD=BC}\)

四角形 \({\rm ABCD}\) に条件を書きこむと、

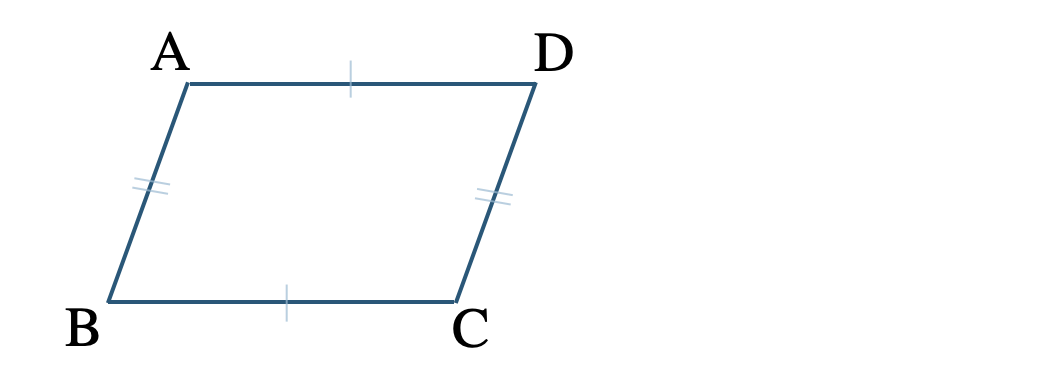
これより、平行四辺形になるための条件「２組の対辺がそれぞれ等しい」となる
したがって、
四角形 \({\rm ABCD}\) は平行四辺形である

問題

次の四角形 \({\rm ABCD}\) が平行四辺形であるか調べよ。

---

\({\small (3)}~\)\(\angle{\rm A}=\angle{\rm C}~,~\angle{\rm B}=\angle{\rm D}\)

四角形 \({\rm ABCD}\) に条件を書きこむと、

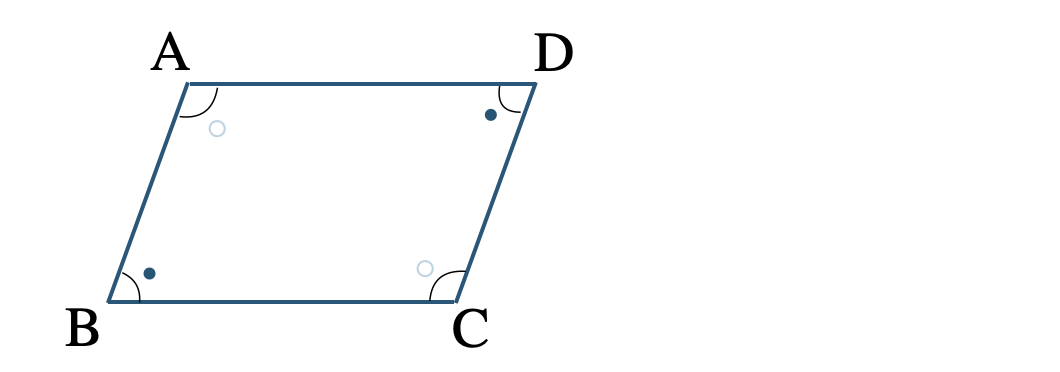
これより、平行四辺形になるための条件「２組の対角がそれぞれ等しい」となる
したがって、
四角形 \({\rm ABCD}\) は平行四辺形である

問題

次の四角形 \({\rm ABCD}\) が平行四辺形であるか調べよ。

---

\({\small (4)}~\)\({\rm AD=BC~,~AB\,//\,CD}\)

四角形 \({\rm ABCD}\) に条件を書きこむと、

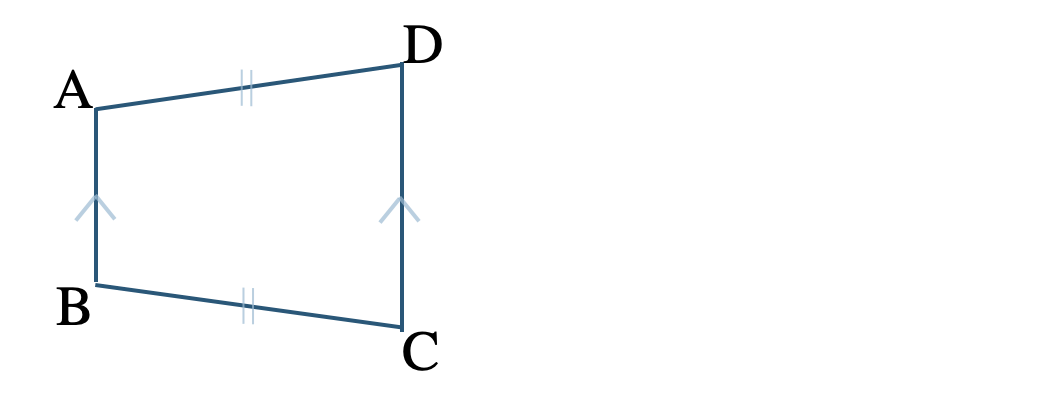
これより、平行四辺形になるための条件にあてはまるものはない
したがって、
四角形 \({\rm ABCD}\) は平行四辺形でない

問題

次の四角形 \({\rm ABCD}\) が平行四辺形であるか調べよ。

---

\({\small (5)}~\)\({\rm AB=BC~,~AD=CD}\)

四角形 \({\rm ABCD}\) に条件を書きこむと、

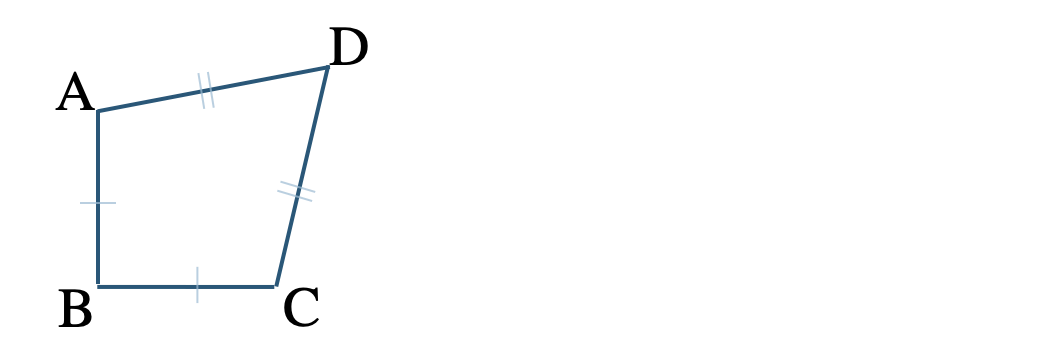
これより、平行四辺形になるための条件にあてはまるものはない
したがって、
四角形 \({\rm ABCD}\) は平行四辺形でない

問題

次の四角形 \({\rm ABCD}\) が平行四辺形であるか調べよ。

---

\({\small (6)}~\)\({\rm AD=BC~,~}\)\(\angle{\rm A}=60^\circ~,~\angle{\rm B}=120^\circ\)

\(\angle{\rm A}=60^\circ~,~\angle{\rm B}=120^\circ\) より、錯角が等しいので \({\rm AD\,//\,BC}\) となる
四角形 \({\rm ABCD}\) に条件を書きこむと、

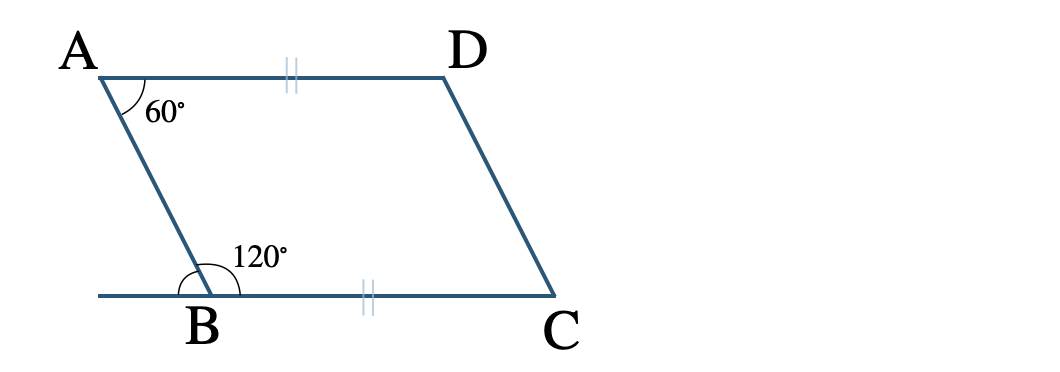
これより、平行四辺形になるための条件「１組の対辺が等しくて平行である」となる
したがって、
四角形 \({\rm ABCD}\) は平行四辺形である