問題:展開・因数分解と表やカレンダー
問題
\({\small (1)}~\)下の図1は、自然数が順番に一段5つずつ並んでいる。このとき、表の中の4つの整数の組(図2)について、\(bc-ad\) の値はつねに \(5\) となることを証明せよ。
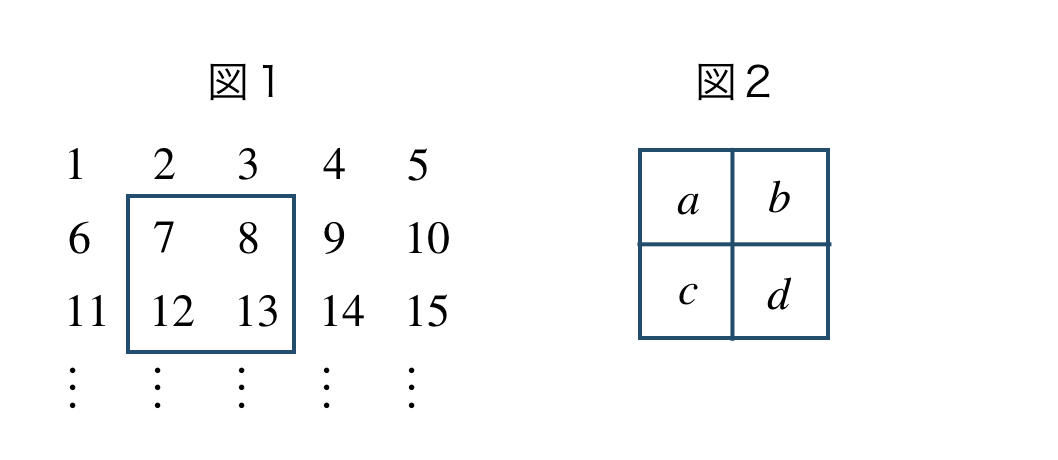
\({\small (2)}~\)下の図3は、ある月のカレンダーである。このとき、カレンダーの中の3つの整数の組(図4)について、\(b^2-ac\) の値はつねに \(49\) となることを証明せよ。
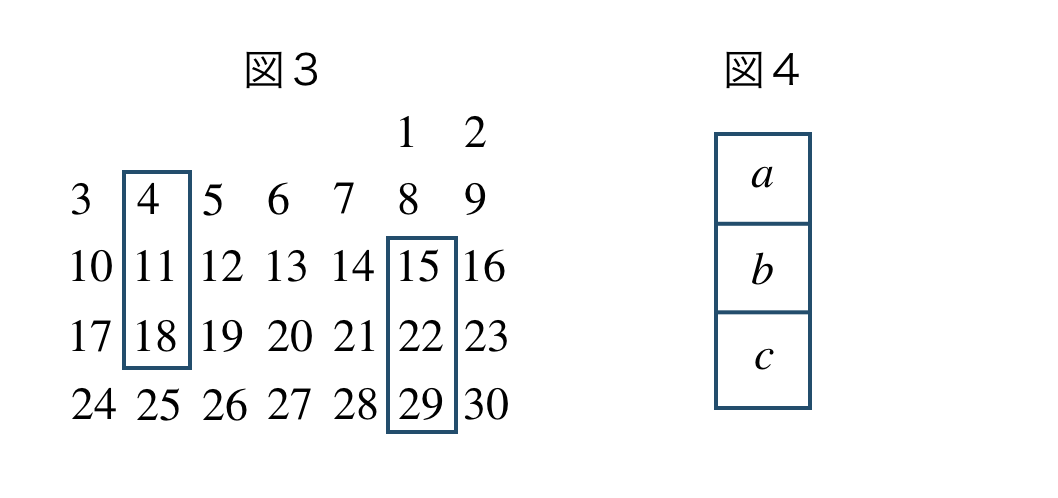
次の問いに答えよ。
\({\small (1)}~\)下の図1は、自然数が順番に一段5つずつ並んでいる。このとき、表の中の4つの整数の組(図2)について、\(bc-ad\) の値はつねに \(5\) となることを証明せよ。
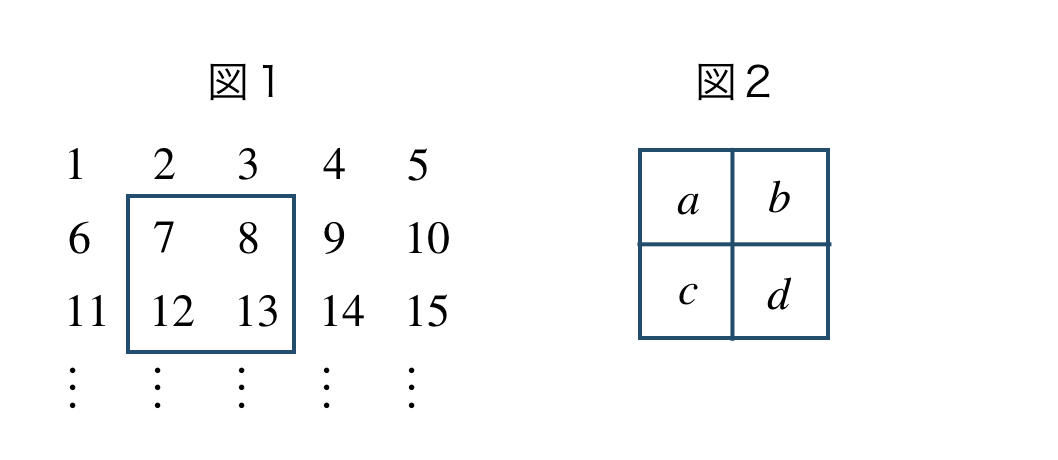
\({\small (2)}~\)下の図3は、ある月のカレンダーである。このとき、カレンダーの中の3つの整数の組(図4)について、\(b^2-ac\) の値はつねに \(49\) となることを証明せよ。
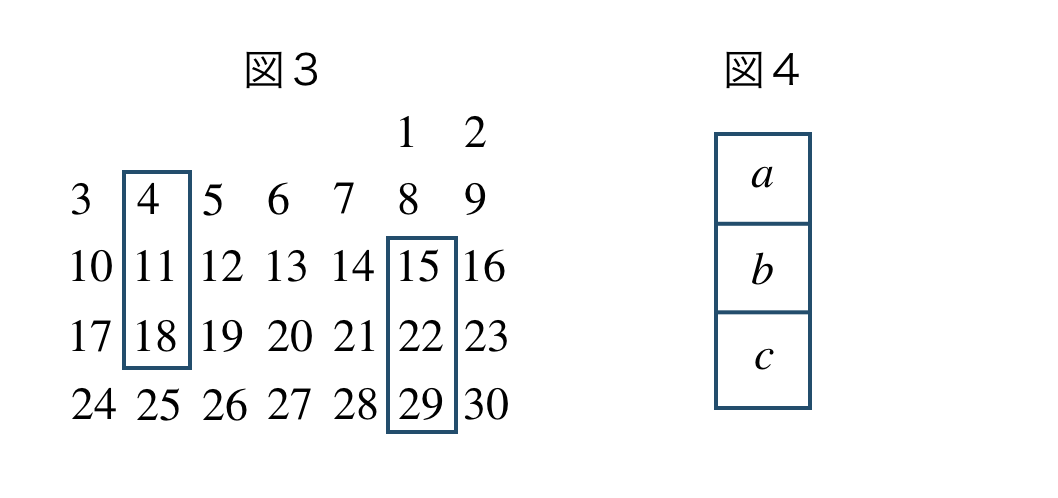
追加の練習問題のページはこちら→
展開・因数分解と表やカレンダー|練習問題20問
解法のPoint
Point:表やカレンダーの規則性
たとえば、カレンダーでは、
真ん中の枠の整数を \(n\) とすると、
左の枠の数は1日前の \(n-1\)
右の枠の数は1日後の \(n+1\)
上の枠の数は1週間前の \(n-7\)
下の枠の数は1週間後の \(n+7\) となる
③ 問題文の式を整数 \(n\) の式で表して計算する。
④ 結論を書く。
→「したがって、◯◯となる」
表やカレンダーの規則性を証明する問題は、
① 整数の組の1つを整数 \(n\) とする。

② 規則性に注意して、残りの枠にあてはまる数を整数 \(n\) を使って表す。
※ 上下や左右の関係に注意する。
たとえば、カレンダーでは、
真ん中の枠の整数を \(n\) とすると、
左の枠の数は1日前の \(n-1\)
右の枠の数は1日後の \(n+1\)
上の枠の数は1週間前の \(n-7\)
下の枠の数は1週間後の \(n+7\) となる
③ 問題文の式を整数 \(n\) の式で表して計算する。
④ 結論を書く。
→「したがって、◯◯となる」
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:展開・因数分解と表やカレンダー
問題解説(1)
問題
\({\small (1)}~\)下の図1は、自然数が順番に一段5つずつ並んでいる。このとき、表の中の4つの整数の組(図2)について、\(bc-ad\) の値はつねに \(5\) となることを証明せよ。
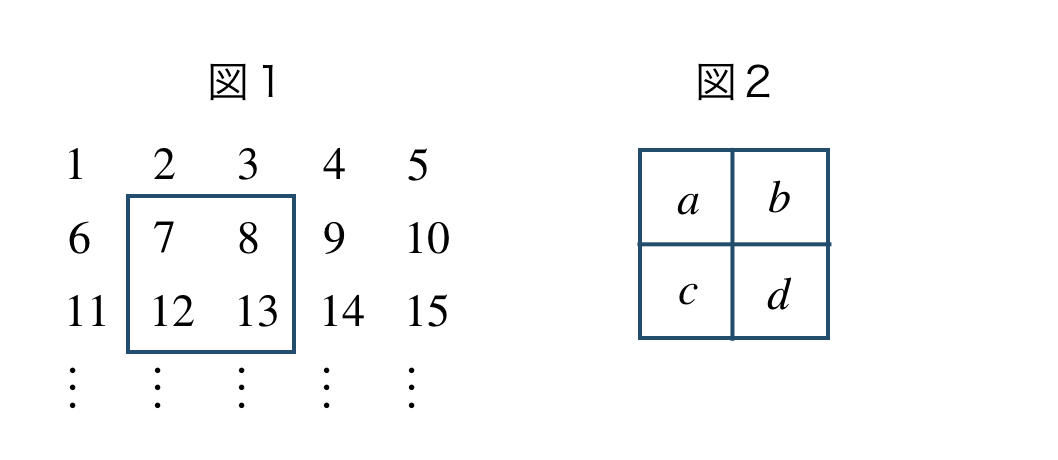
次の問いに答えよ。
\({\small (1)}~\)下の図1は、自然数が順番に一段5つずつ並んでいる。このとき、表の中の4つの整数の組(図2)について、\(bc-ad\) の値はつねに \(5\) となることを証明せよ。
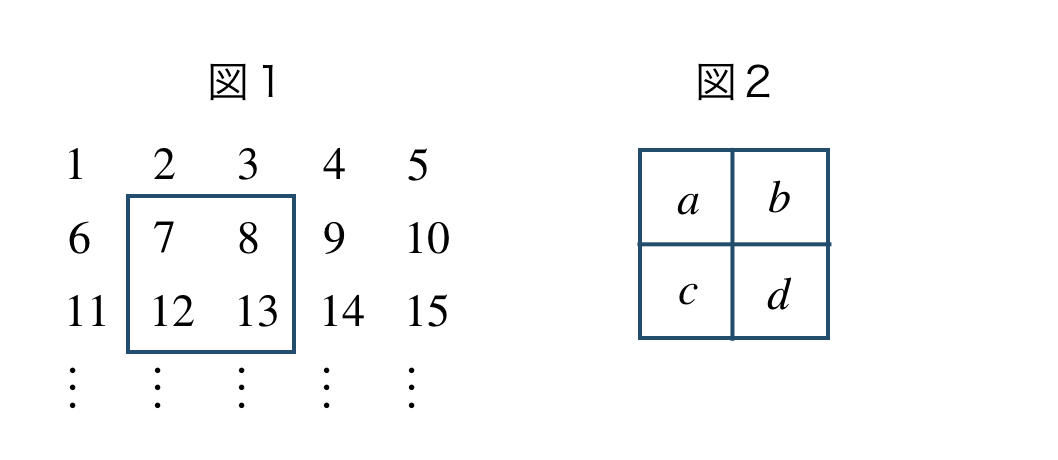
[証明] 整数 \(n\) を用いて、左上を \(a=n\) とすると、
\(b\) は \(a\) の右隣で \(+1\) されて、\(b=n+1\)
\(c\) は \(a\) の一段下で \(+5\) されて、\(c=n+5\)
\(d\) は \(a\) の一段下の右隣で \(+6\) されて、\(d=n+6\)

よって、\(bc-ad\) は、
※ ( ) を付けたまま代入する。
\(\begin{split}&bc-ad\\[2pt]~~=~&(n+1)(n+5)-n(n+6)\end{split}\)
それぞれを展開すると、
※ この枠の中の計算は書かないでよい。
\((n+1)(n+5)\) は乗法の公式より、
\(\begin{split}&(n+1)(n+5)\\[2pt]~~=~&n^2+(1+5)n+1\times5\\[2pt]~~=~&n^2+6n+5\end{split}\)
\(n(n+6)\) は分配法則より、
\(\begin{split}&n(n+6)\\[2pt]~~=~&n\times n+n\times 6\\[2pt]~~=~&n^2+6n\end{split}\)
これより、( ) を付けたまま展開すると、
\((n+1)(n+5)\) は乗法の公式より、
\(\begin{split}&(n+1)(n+5)\\[2pt]~~=~&n^2+(1+5)n+1\times5\\[2pt]~~=~&n^2+6n+5\end{split}\)
\(n(n+6)\) は分配法則より、
\(\begin{split}&n(n+6)\\[2pt]~~=~&n\times n+n\times 6\\[2pt]~~=~&n^2+6n\end{split}\)
これより、( ) を付けたまま展開すると、
\(\begin{split}~~=~&(n^2+6n+5)-(n^2+6n)\\[2pt]~~=~&n^2+6n+5-n^2-6n\\[2pt]~~=~&(n^2-n^2)+(6n-6n)+5\\[2pt]~~=~&5\end{split}\)
したがって、\(bc-ad\) の値はつねに \(5\) となる [終]
問題解説(2)
問題
\({\small (2)}~\)下の図3は、ある月のカレンダーである。このとき、カレンダーの中の3つの整数の組(図4)について、\(b^2-ac\) の値はつねに \(49\) となることを証明せよ。
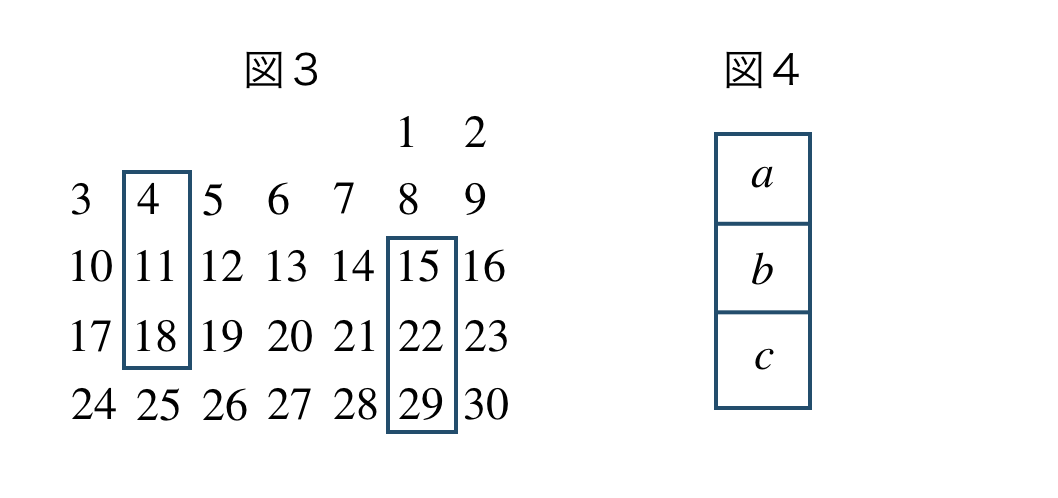
次の問いに答えよ。
\({\small (2)}~\)下の図3は、ある月のカレンダーである。このとき、カレンダーの中の3つの整数の組(図4)について、\(b^2-ac\) の値はつねに \(49\) となることを証明せよ。
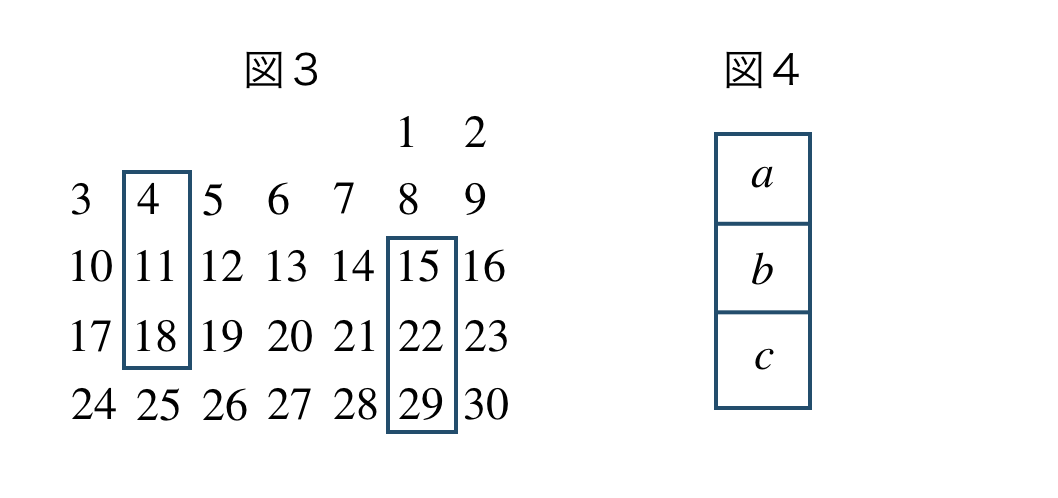
[証明] 整数 \(n\) を用いて、中央を \(b=n\) とすると、
\(a\) は \(b\) の一段上で \(-7\) されて、\(a=n-7\)
\(c\) は \(b\) の一段下で \(+7\) されて、\(c=n+7\)

よって、\(b^2-ac\) は、
※ ( ) を付けたまま代入する。
\(\begin{split}&b^2-ac\\[2pt]~~=~&n^2-(n-7)(n+7)\end{split}\)
展開すると、
※ この枠の中の計算は書かないでよい。
\((n-7)(n+7)\) は2乗ー2乗の乗法の公式より、
\(\begin{split}&(n-7)(n+7)\\[2pt]~~=~&n^2-7^2\\[2pt]~~=~&n^2-49\end{split}\)
これより、( ) を付けたまま展開すると、
\((n-7)(n+7)\) は2乗ー2乗の乗法の公式より、
\(\begin{split}&(n-7)(n+7)\\[2pt]~~=~&n^2-7^2\\[2pt]~~=~&n^2-49\end{split}\)
これより、( ) を付けたまま展開すると、
\(\begin{split}~~=~&n^2-(n^2-49)\\[2pt]~~=~&n^2-n^2+49\\[2pt]~~=~&49\end{split}\)
したがって、\(b^2-ac\) の値はつねに \(49\) となる [終]
追加の練習問題のページはこちら→
展開・因数分解と表やカレンダー|練習問題20問

【問題一覧】中3|展開と因数分解
このページは「中学数学3 展開と因数分解」の問題一覧ページとなります。解説の見たい単元名がわからない...


