このページでは、「展開・因数分解と表やカレンダー」をテストに直結する形で練習できます。各問は[解答を見る]からすぐに答えを確認できます。
- 対象:中学数学(教科書レベル)/授業の復習やテスト前の確認にぴったり
- レベル:基本問題を中心にそろえてあるので、安心して取り組めます
- 使い方:全部を解く必要はなく、理解できたと思えるところまで進めれば大丈夫です
- 利用方法:学校や塾での小テスト、家庭学習のプリントなどにも自由にお使いいただけます
【中学数学】展開・因数分解と表やカレンダーの練習問題20問
この問題の解き方の詳細は↓
展開・因数分解と表やカレンダーの解法まとめ で確認できます。
次の表の中の上下2つの整数について、\(b^2-a^2\) が \(5\) の倍数となることを証明せよ。
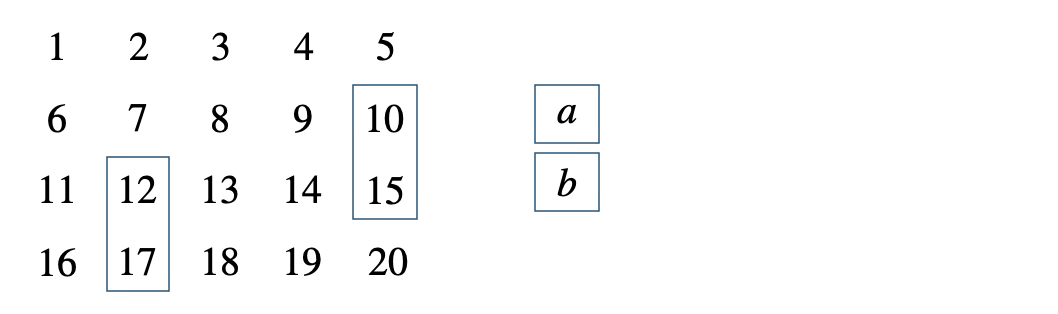
[ 解答を見る ]
[証明] 整数 \(n\) を用いて、上を \(a=n\) とすると、\(b=n+5\)
よって、\(b^2-a^2\) は、
\(\begin{split}&b^2-a^2\\[2pt]~~=~&(n+5)^2-n^2\\[2pt]~~=~&n^2+10n+25-n^2\\[2pt]~~=~&10n+25\\[2pt]~~=~&5(2n+5)\end{split}\)
\(2n+5\) は整数より、\(b^2-a^2\) は \(5\) の倍数となる [終]
次の表の中の上下2つの整数について、\(b^2-ab\) が \(5\) の倍数となることを証明せよ。
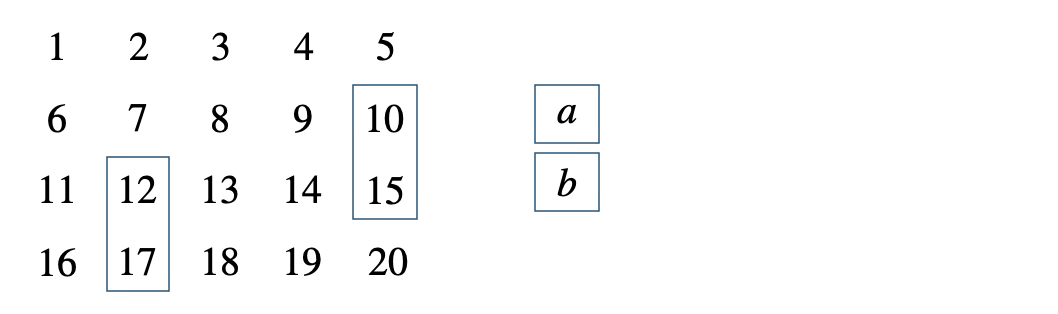
[ 解答を見る ]
[証明] 整数 \(n\) を用いて、上を \(a=n\) とすると、\(b=n+5\)
よって、\(b^2-ab\) は、
\(\begin{split}&b^2-ab\\[2pt]~~=~&(n+5)^2-n(n+5)\\[2pt]~~=~&n^2+10n+25-(n^2+5n)\\[2pt]~~=~&5n+25\\[2pt]~~=~&5(n+5)\end{split}\)
\(n+5\) は整数より、\(b^2-ab\) は \(5\) の倍数となる [終]
次の表の中の縦に並ぶ3つの整数について、\(b^2-ac\) がつねに \(25\) となることを証明せよ。
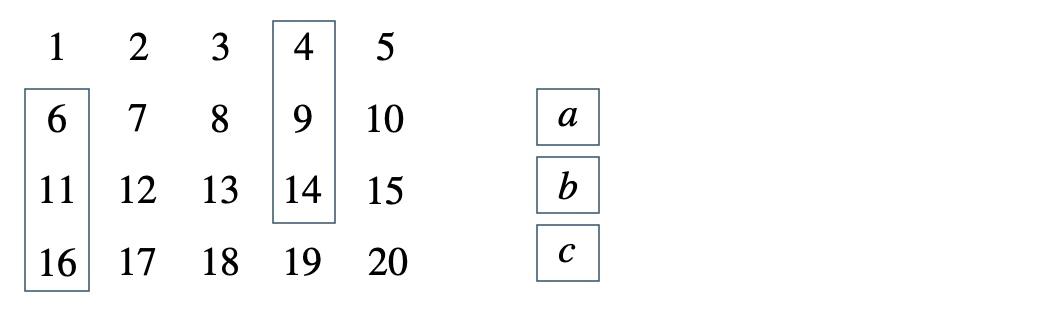
[ 解答を見る ]
[証明] 整数 \(n\) を用いて、真ん中を \(b=n\) とすると、\(a=n-5~,~c=n+5\)
よって、\(b^2-ac\) は、
\(\begin{split}&b^2-ac\\[2pt]~~=~&n^2-(n-5)(n+5)\\[2pt]~~=~&n^2-(n^2-25)\\[2pt]~~=~&25\end{split}\)
したがって、つねに \(25\) となる [終]
次の表の中の縦に並ぶ3つの整数について、\(bc-ab\) が \(10\) の倍数となることを証明せよ。

[ 解答を見る ]
[証明] 整数 \(n\) を用いて、真ん中を \(b=n\) とすると、\(a=n-5~,~c=n+5\)
よって、\(bc-ab\) は、
\(\begin{split}&bc-ab\\[2pt]~~=~&n(n+5)-(n-5)n\\[2pt]~~=~&n^2+5n-(n^2-5n)\\[2pt]~~=~&10n\end{split}\)
\(n\) は整数より、\(bc-ab\) は \(10\) の倍数となる [終]
次の表の中の正方形の4つの整数について、\(cd-ab\) が \(10\) の倍数となることを証明せよ。
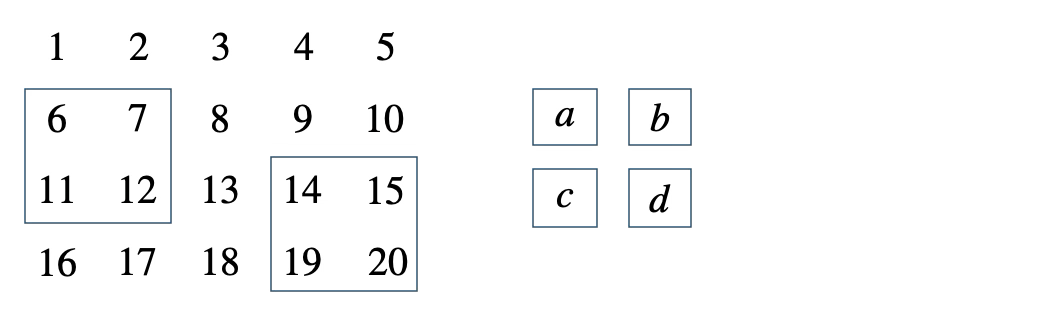
[ 解答を見る ]
[証明] 整数 \(n\) を用いて、左上を \(a=n\) とすると、
\(b=n+1~,~c=n+5~,~d=n+6\) となる
よって、\(cd-ab\) は、
\(\begin{split}&cd-ab\\[2pt]~~=~&(n+5)(n+6)-n(n+1)\\[2pt]~~=~&n^2+11n+30-(n^2+n)\\[2pt]~~=~&10n+30\\[2pt]~~=~&10(n+3)\end{split}\)
\(n+3\) は整数より、\(cd-ab\) は \(10\) の倍数となる [終]
次の表の中の正方形の4つの整数について、\(bd-ac\) が \(2\) の倍数となることを証明せよ。

[ 解答を見る ]
[証明] 整数 \(n\) を用いて、左上を \(a=n\) とすると、
\(b=n+1~,~c=n+5~,~d=n+6\) となる
よって、\(bd-ac\) は、
\(\begin{split}&bd-ac\\[2pt]~~=~&(n+1)(n+6)-n(n+5)\\[2pt]~~=~&n^2+7n+6-(n^2+5n)\\[2pt]~~=~&2n+6\\[2pt]~~=~&2(n+3)\end{split}\)
\(n+3\) は整数より、\(bd-ac\) は \(2\) の倍数となる [終]
次のカレンダーの中の上下2つの整数について、\(b^2-a^2\) が \(7\) の倍数となることを証明せよ。
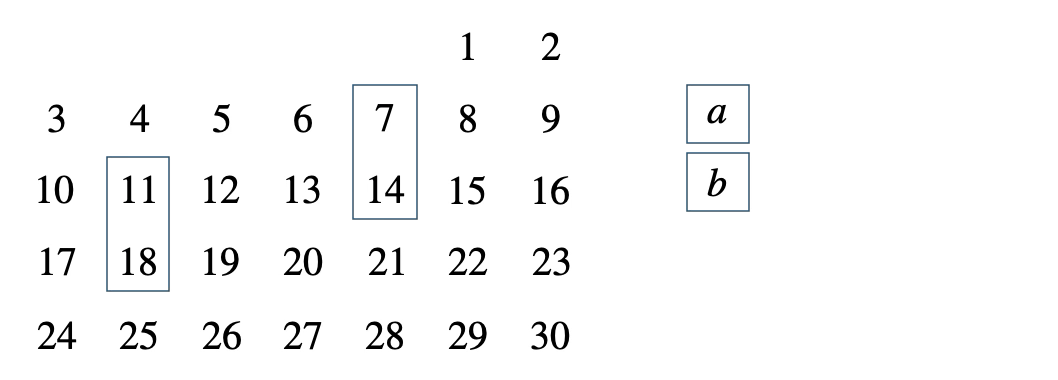
[ 解答を見る ]
[証明] 整数 \(n\) を用いて、上を \(a=n\) とすると、\(b=n+7\)
よって、\(b^2-a^2\) は、
\(\begin{split}&b^2-a^2\\[2pt]~~=~&(n+7)^2-n^2\\[2pt]~~=~&n^2+14n+49-n^2\\[2pt]~~=~&14n+49\\[2pt]~~=~&7(2n+7)\end{split}\)
\(2n+7\) は整数より、\(b^2-a^2\) は \(7\) の倍数となる [終]
次のカレンダーの中の上下2つの整数について、\(b^2-ab\) が \(7\) の倍数となることを証明せよ。
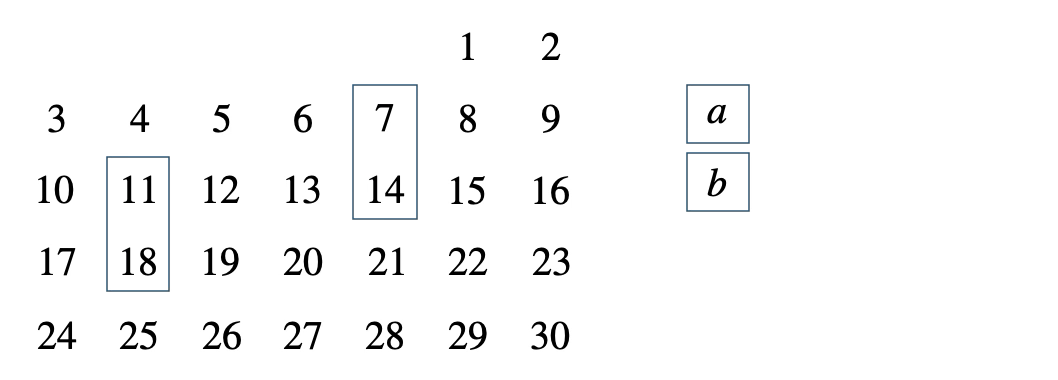
[ 解答を見る ]
[証明] 整数 \(n\) を用いて、上を \(a=n\) とすると、\(b=n+7\)
よって、\(b^2-ab\) は、
\(\begin{split}&b^2-ab\\[2pt]~~=~&(n+7)^2-n(n+7)\\[2pt]~~=~&n^2+14n+49-(n^2+7n)\\[2pt]~~=~&7n+49\\[2pt]~~=~&7(n+7)\end{split}\)
\(n+7\) は整数より、\(b^2-ab\) は \(7\) の倍数となる [終]
次のカレンダーの中の縦に並ぶ3つの整数について、\(bc-ab\) が \(14\) の倍数となることを証明せよ。
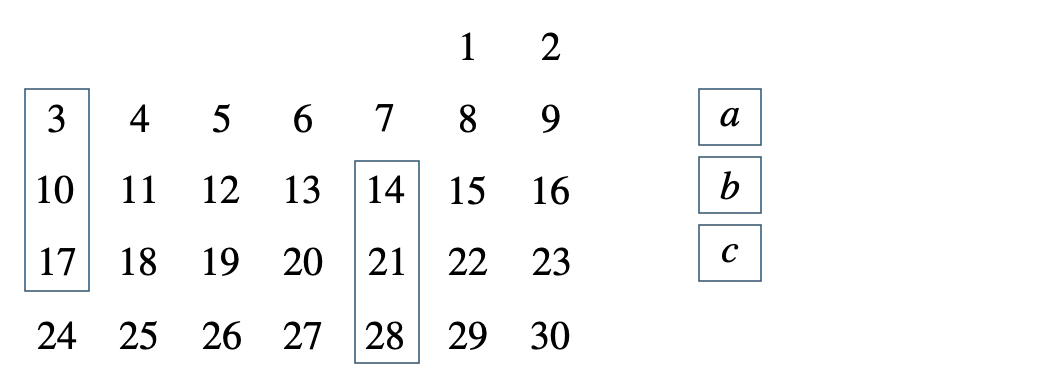
[ 解答を見る ]
[証明] 整数 \(n\) を用いて、真ん中を \(b=n\) とすると、\(a=n-7~,~c=n+7\)
よって、\(bc-ab\) は、
\(\begin{split}&bc-ab\\[2pt]~~=~&n(n+7)-(n-7)n\\[2pt]~~=~&n^2+7n-(n^2-7n)\\[2pt]~~=~&14n\end{split}\)
\(n\) は整数より、\(bc-ab\) は \(14\) の倍数となる [終]
次のカレンダーの中の横に並ぶ3つの整数について、\(b^2-ac\) がつねに \(1\) となることを証明せよ。
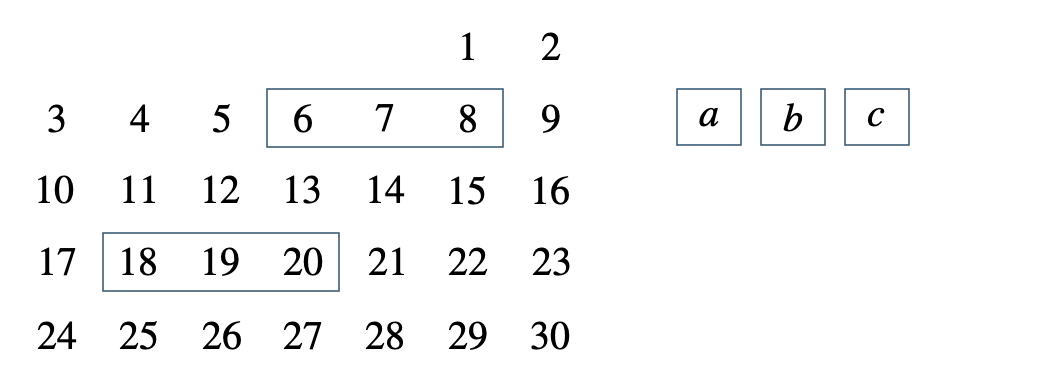
[ 解答を見る ]
[証明] 整数 \(n\) を用いて、左を \(a=n\) とすると、\(b=n+1~,~c=n+2\)
よって、\(b^2-ac\) は、
\(\begin{split}&b^2-ac\\[2pt]~~=~&(n+1)^2-n(n+2)\\[2pt]~~=~&n^2+2n+1-(n^2+2n)\\[2pt]~~=~&1\end{split}\)
したがって、つねに \(1\) となる [終]
次のカレンダーの中の正方形の4つの整数について、\(bc-ad\) がつねに \(7\) となることを証明せよ。
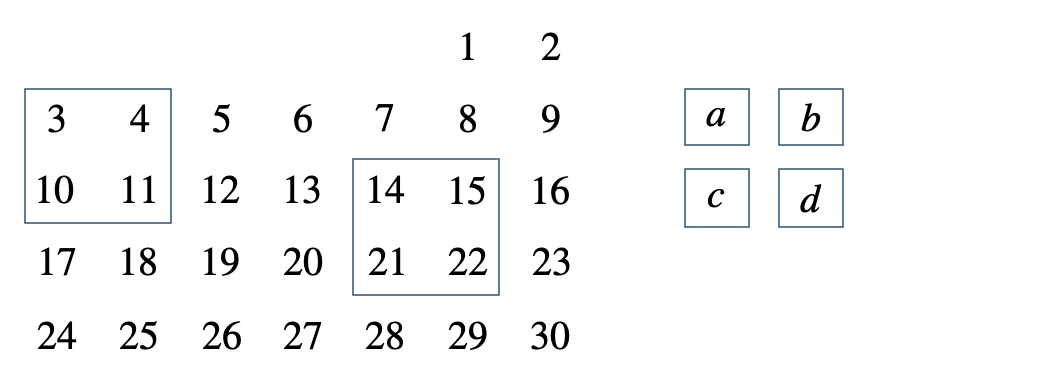
[ 解答を見る ]
[証明] 整数 \(n\) を用いて、左上を \(a=n\) とすると、
\(b=n+1~,~c=n+7~,~d=n+8\) となる
よって、\(bc-ad\) は、
\(\begin{split}&bc-ad\\[2pt]~~=~&(n+1)(n+7)-n(n+8)\\[2pt]~~=~&n^2+8n+7-(n^2+8n)\\[2pt]~~=~&7\end{split}\)
したがって、つねに \(7\) となる [終]
次のカレンダーの中の正方形の4つの整数について、\(cd-ab\) が \(14\) の倍数となることを証明せよ。

[ 解答を見る ]
[証明] 整数 \(n\) を用いて、左上を \(a=n\) とすると、
\(b=n+1~,~c=n+7~,~d=n+8\) となる
よって、\(cd-ab\) は、
\(\begin{split}&cd-ab\\[2pt]~~=~&(n+7)(n+8)-n(n+1)\\[2pt]~~=~&n^2+15n+56-(n^2+n)\\[2pt]~~=~&14n+56\\[2pt]~~=~&14(n+4)\end{split}\)
\(n+4\) は整数より、\(cd-ab\) は \(14\) の倍数となる [終]
次のカレンダーの中の正方形の4つの整数について、\(bd-ac\) が \(2\) の倍数となることを証明せよ。

[ 解答を見る ]
[証明] 整数 \(n\) を用いて、左上を \(a=n\) とすると、
\(b=n+1~,~c=n+7~,~d=n+8\) となる
よって、\(bd-ac\) は、
\(\begin{split}&bd-ac\\[2pt]~~=~&(n+1)(n+8)-n(n+7)\\[2pt]~~=~&n^2+9n+8-(n^2+7n)\\[2pt]~~=~&2n+8\\[2pt]~~=~&2(n+4)\end{split}\)
\(n+4\) は整数より、\(bd-ac\) は \(2\) の倍数となる [終]
次の表の中の上下2つの整数について、\(b^2-a^2\) が \(12\) の倍数となることを証明せよ。
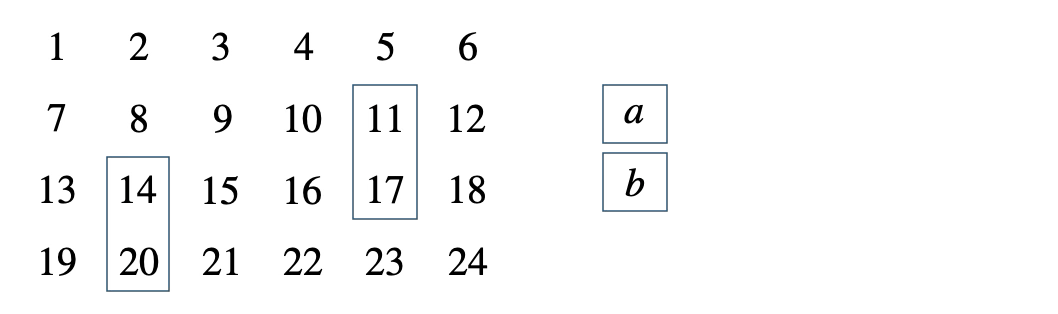
[ 解答を見る ]
[証明] 整数 \(n\) を用いて、上を \(a=n\) とすると、\(b=n+6\)
よって、\(b^2-a^2\) は、
\(\begin{split}&b^2-a^2\\[2pt]~~=~&(n+6)^2-n^2\\[2pt]~~=~&n^2+12n+36-n^2\\[2pt]~~=~&12n+36\\[2pt]~~=~&12(n+3)\end{split}\)
\(n+3\) は整数より、\(b^2-a^2\) は \(12\) の倍数となる [終]
次の表の中の上下2つの整数について、\(b^2-ab\) が \(6\) の倍数となることを証明せよ。
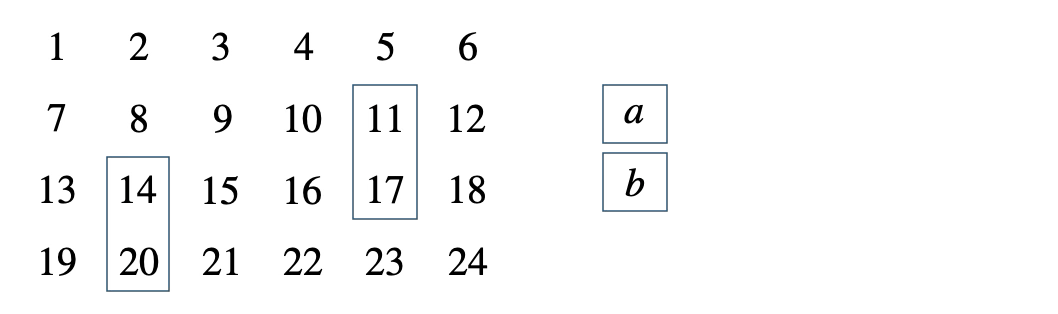
[ 解答を見る ]
[証明] 整数 \(n\) を用いて、上を \(a=n\) とすると、\(b=n+6\)
よって、\(b^2-ab\) は、
\(\begin{split}&b^2-ab\\[2pt]~~=~&(n+6)^2-n(n+6)\\[2pt]~~=~&n^2+12n+36-(n^2+6n)\\[2pt]~~=~&6n+36\\[2pt]~~=~&6(n+6)\end{split}\)
\(n+6\) は整数より、\(b^2-ab\) は \(6\) の倍数となる [終]
次の表の中の縦に並ぶ3つの整数について、\(b^2-ac\) がつねに \(36\) となることを証明せよ。
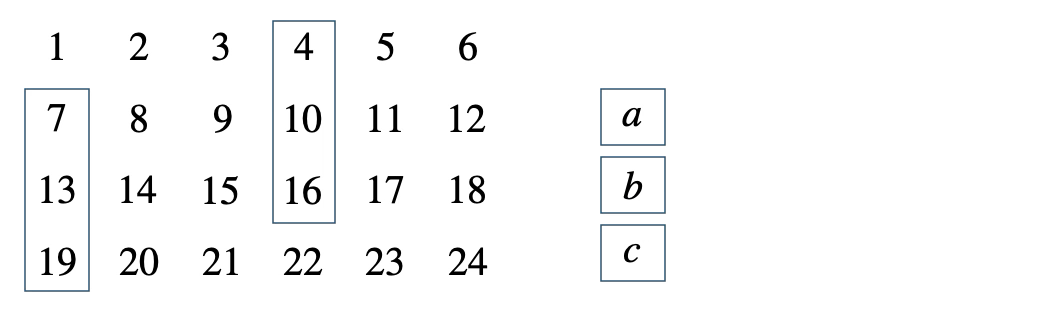
[ 解答を見る ]
[証明] 整数 \(n\) を用いて、真ん中を \(b=n\) とすると、\(a=n-6~,~c=n+6\)
よって、\(b^2-ac\) は、
\(\begin{split}&b^2-ac\\[2pt]~~=~&n^2-(n-6)(n+6)\\[2pt]~~=~&n^2-(n^2-36)\\[2pt]~~=~&36\end{split}\)
したがって、つねに \(36\) となる [終]
次の表の中の縦に並ぶ3つの整数について、\(bc-ad\) が \(12\) の倍数となることを証明せよ。

[ 解答を見る ]
[証明] 整数 \(n\) を用いて、左上を \(a=n-6\)、右上を \(b=n-5\)、左下を \(c=n+6\)、右下を \(d=n+7\) とする(同じ列の上と下は \(+12\) の関係)。
よって、\(bc-ad\) は、
\(\begin{split}&bc-ad\\[2pt]~~=~&(n-5)(n+6)-(n-6)(n+7)\\[2pt]~~=~&n^2+n-30-(n^2+n-42)\\[2pt]~~=~&12\end{split}\)
よって、\(bc-ad\) は \(12\)(すなわち \(12\) の倍数)となる [終]
次の表の中の横に並ぶ3つの整数について、\(bc-ab\) が \(2\) の倍数となることを証明せよ。
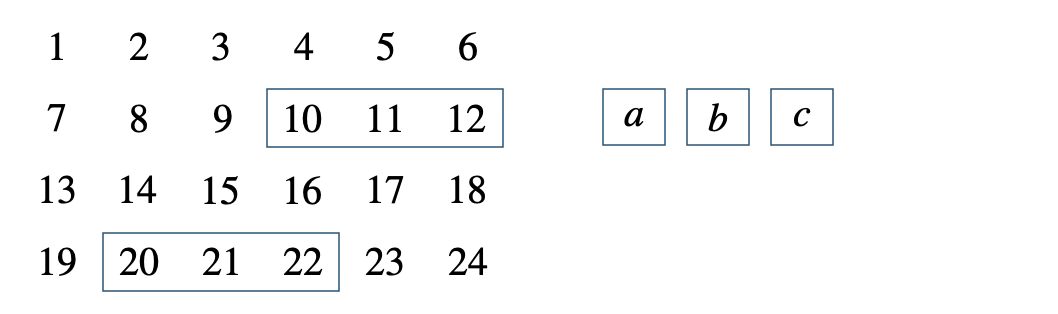
[ 解答を見る ]
[証明] 整数 \(n\) を用いて、左を \(a=n\) とすると、\(b=n+1~,~c=n+2\)
よって、\(bc-ab\) は、
\(\begin{split}&bc-ab\\[2pt]~~=~&(n+1)(n+2)-n(n+1)\\[2pt]~~=~&n^2+3n+2-(n^2+n)\\[2pt]~~=~&2n+2\\[2pt]~~=~&2(n+1)\end{split}\)
\(n+1\) は整数より、\(bc-ab\) は \(2\) の倍数となる [終]
次の表の中の正方形の4つの整数について、\(bc-ad\) がつねに \(6\) となることを証明せよ。
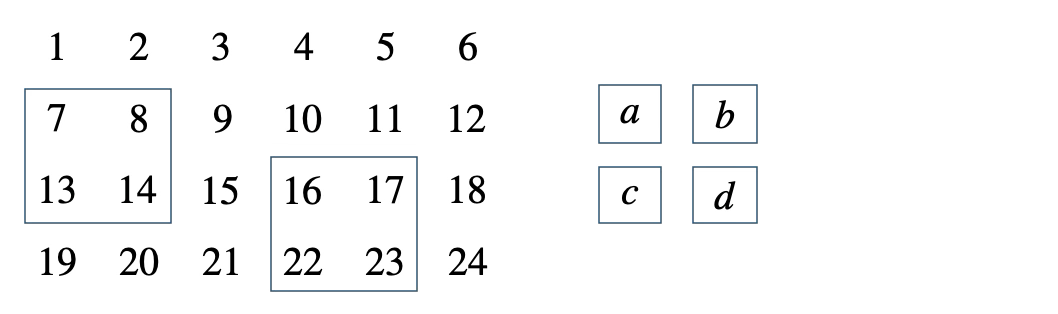
[ 解答を見る ]
[証明] 整数 \(n\) を用いて、左上を \(a=n\) とすると、
\(b=n+1~,~c=n+6~,~d=n+7\) となる
よって、\(bc-ad\) は、
\(\begin{split}&bc-ad\\[2pt]~~=~&(n+1)(n+6)-n(n+7)\\[2pt]~~=~&n^2+7n+6-(n^2+7n)\\[2pt]~~=~&6\end{split}\)
したがって、つねに \(6\) となる [終]
次の表の中の正方形の4つの整数について、\(cd-ab\) が \(6\) の倍数となることを証明せよ。

[ 解答を見る ]
[証明] 整数 \(n\) を用いて、左上を \(a=n\) とすると、
\(b=n+1~,~c=n+6~,~d=n+7\) となる
よって、\(cd-ab\) は、
\(\begin{split}&cd-ab\\[2pt]~~=~&(n+6)(n+7)-n(n+1)\\[2pt]~~=~&n^2+13n+42-(n^2+n)\\[2pt]~~=~&12n+42\\[2pt]~~=~&6(2n+7)\end{split}\)
\(2n+7\) は整数より、\(cd-ab\) は \(6\) の倍数となる [終]



