問題:平方根と不等式
問題
\(\begin{split}{\small (1)}~2\lt\sqrt{a}≦3\end{split}\)
\(\begin{split}{\small (2)}~1.7\lt\sqrt{a}\lt2.2\end{split}\)
\(\begin{split}{\small (3)}~\sqrt{5}≦a\lt\sqrt{20}\end{split}\)
\(\begin{split}{\small (4)}~\sqrt{50}\lt a \lt\sqrt{80}\end{split}\)
\(a\) が自然数のとき、次の式にあてはまる \(a\) の値をすべて求めよ。
\(\begin{split}{\small (1)}~2\lt\sqrt{a}≦3\end{split}\)
\(\begin{split}{\small (2)}~1.7\lt\sqrt{a}\lt2.2\end{split}\)
\(\begin{split}{\small (3)}~\sqrt{5}≦a\lt\sqrt{20}\end{split}\)
\(\begin{split}{\small (4)}~\sqrt{50}\lt a \lt\sqrt{80}\end{split}\)
解法のPoint
Point:平方根と不等式
① それぞれの辺を2乗した不等式をつくる。
\(\left(\sqrt{a}\right)^2=a\) より、 \(1≦a\lt 4\)
② この不等式を満たす自然数 \(a\) を見つける。
※ 数直線上に不等式を表すとわかりやすい。

これより、\(a=1~,~2~,~3\)
■ \(\sqrt{3}\lt a≦\sqrt{10}\) の場合 ( \(a\) は自然数 )
① それぞれの辺を2乗した不等式をつくる。
\(3\lt a^2≦ 10\)
② この不等式を満たす自然数 \(a\) を見つける。
\(a\) と \(a^2\) の関係を書き並べると、
\(\begin{split}&a=1~,~2~,~3~,~4~,~5~,~6~,~\cdots\\[2pt]~~~~~&a^2=1~,~4~,~9~,~16~,~25~,~36~,~\cdots\end{split}\)
不等式を満たす \(a^2\) は \(a^2=4~,~9\)
よって、\(a\) の値は \(a=2~,~3\)
■ \(1≦\sqrt{a}\lt 2\) の場合 ( \(a\) は自然数 )
① それぞれの辺を2乗した不等式をつくる。
\(\left(\sqrt{a}\right)^2=a\) より、 \(1≦a\lt 4\)
② この不等式を満たす自然数 \(a\) を見つける。
※ 数直線上に不等式を表すとわかりやすい。

これより、\(a=1~,~2~,~3\)
■ \(\sqrt{3}\lt a≦\sqrt{10}\) の場合 ( \(a\) は自然数 )
① それぞれの辺を2乗した不等式をつくる。
\(3\lt a^2≦ 10\)
② この不等式を満たす自然数 \(a\) を見つける。
\(a\) と \(a^2\) の関係を書き並べると、
\(\begin{split}&a=1~,~2~,~3~,~4~,~5~,~6~,~\cdots\\[2pt]~~~~~&a^2=1~,~4~,~9~,~16~,~25~,~36~,~\cdots\end{split}\)
不等式を満たす \(a^2\) は \(a^2=4~,~9\)
よって、\(a\) の値は \(a=2~,~3\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:平方根と不等式
問題解説(1)
問題
\(\begin{split}{\small (1)}~2\lt\sqrt{a}≦3\end{split}\)
\(a\) が自然数のとき、次の式にあてはまる \(a\) の値をすべて求めよ。
\(\begin{split}{\small (1)}~2\lt\sqrt{a}≦3\end{split}\)
それぞれの辺を2乗すると、
\(\begin{split}2^2< ~&\left ( \sqrt{a} \right)^2 ≦ 3^2\\[2pt]~~~4< ~&a ≦ 9\end{split}\)
この不等式を数直線上に表すと、

よって、この範囲の自然数を読み取ると、\(a=4\) は含まれず \(a=9\) は含むことより、
答えは、
\(~~~a=5~,~6~,~7~,~8~,~9\)
となる
問題解説(2)
問題
\(\begin{split}{\small (2)}~1.7\lt\sqrt{a}\lt2.2\end{split}\)
\(a\) が自然数のとき、次の式にあてはまる \(a\) の値をすべて求めよ。
\(\begin{split}{\small (2)}~1.7\lt\sqrt{a}\lt2.2\end{split}\)
それぞれの辺を2乗すると、
\(\begin{split}(1.7)^2< ~&\left( \sqrt{a} \right)^2 < (2.2)^2\\[2pt]~~~2.89< ~&a < 4.84\end{split}\)
この不等式を数直線上に表すと、
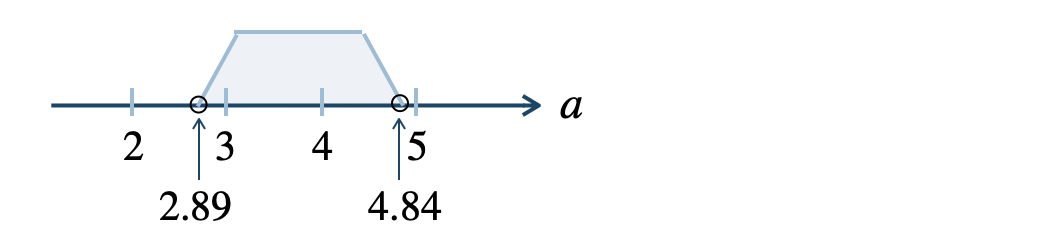
よって、この範囲の自然数を読み取ると、
答えは、\(a=3~,~4\) となる
問題解説(3)
問題
\(\begin{split}{\small (3)}~\sqrt{5}≦a\lt\sqrt{20}\end{split}\)
\(a\) が自然数のとき、次の式にあてはまる \(a\) の値をすべて求めよ。
\(\begin{split}{\small (3)}~\sqrt{5}≦a\lt\sqrt{20}\end{split}\)
それぞれの辺を2乗すると、
\(\begin{split}\left(\sqrt{5}\right)^2≦ ~&\left( \sqrt{a} \right)^2 ≦ \left(\sqrt{20}\right)^2\\[2pt]~~~5≦ ~&a^2 ≦ 20\end{split}\)
ここで、自然数 \(a\) と \(a^2\) の値の関係は、
\(\begin{split}&a=1~,~2~,~3~,~4~,~5~,~6~,~7\\[2pt]~~~&a^2=1~,~4~,~9~,~16~,~25~,~36~,~49\end{split}\)
これより、不等式 \(5≦ a^2 ≦ 20\) を満たすものは、
\(~~~a^2=9~,~16\)
よって、\(a\) の値は、
\(~~~a=3~,~4\)
したがって、答えは \(a=3~,~4\) となる
問題解説(4)
問題
\(\begin{split}{\small (4)}~\sqrt{50}\lt a \lt\sqrt{80}\end{split}\)
\(a\) が自然数のとき、次の式にあてはまる \(a\) の値をすべて求めよ。
\(\begin{split}{\small (4)}~\sqrt{50}\lt a \lt\sqrt{80}\end{split}\)
それぞれの辺を2乗すると、
\(\begin{split}\left(\sqrt{50}\right)^2< ~&\left( \sqrt{a} \right)^2 < \left(\sqrt{80}\right)^2\\[2pt]~~~50< ~&a^2 < 80\end{split}\)
ここで、自然数 \(a\) と \(a^2\) の値の関係は、
\(\begin{split}&a=5~,~6~,~7~,~8~,~9~,~10\\[2pt]~~~&a^2=25~,~36~,~49~,~64~,~81~,~100\end{split}\)
これより、不等式 \(50< a^2 < 80\) を満たすものは、
\(~~~a^2=64\)
よって、\(a\) の値は、
\(~~~a=8\)
したがって、答えは \(a=8\) となる

【問題一覧】中3|平方根
このページは「中学数学3 平方根」の問題一覧ページとなります。解説の見たい単元名がわからないときは、...


