問題:2次方程式と容積
問題

横の長さが縦の長さより \(5~{\rm cm}\) 長い長方形の紙がある。この紙の四すみから1辺 \(2~{\rm cm}\) の正方形を切り取って、ふたのない箱を作った。
箱の容積が \(132~{\rm cm}^3\) となるとき、もとの長方形の縦の長さと横の長さを求めよ。

解法のPoint
Point:2次方程式と容積
① 縦の長さと横の長さを文字で表す。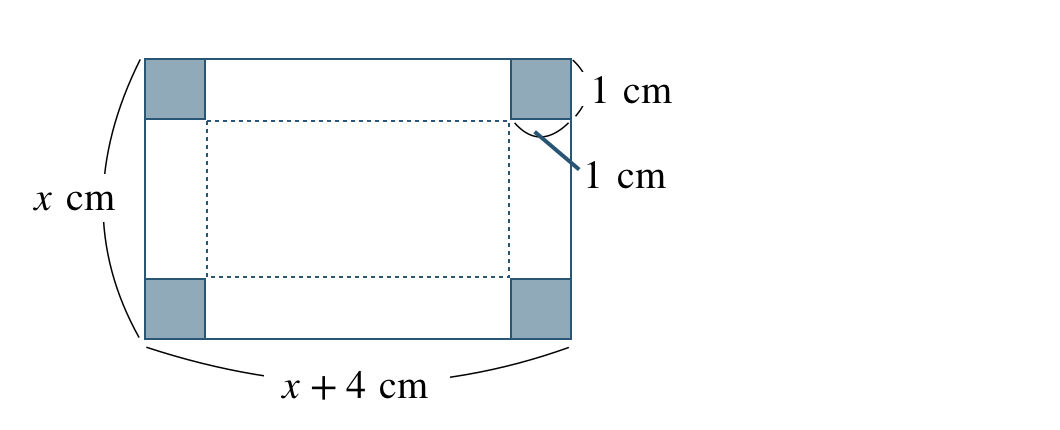
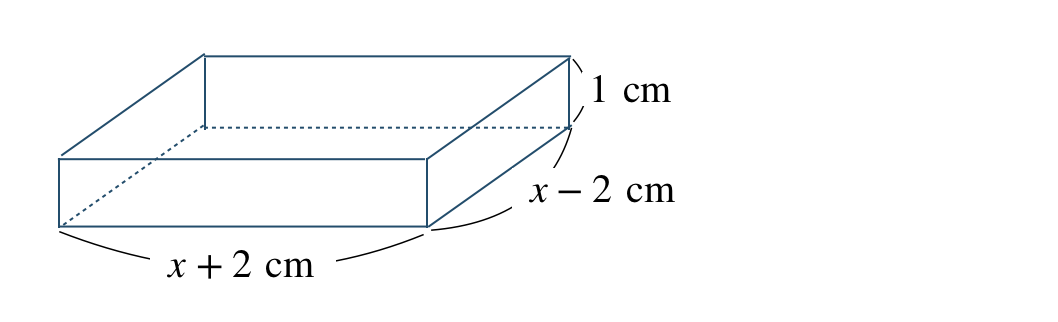
体積が \(60~{\rm cm}^3\) であるので、
\(\begin{split}~~~(x+2){\, \small \times \,}(x-2){\, \small \times \,}1=60\end{split}\)
④ この2次方程式を解く。
⑤ 解が問題に適していることを確認する。
横が縦より \(4~{\rm cm}\) 長い長方形の四すみを1辺 \(1~{\rm cm}\) の正方形を切り取り、\(60~{\rm cm}^3\) の箱を作ったときの縦の長さは、
① 縦の長さと横の長さを文字で表す。

② 箱にしたときの底面の縦の長さ、横の長さと高さを求める。

③ 体積の式を求める。
体積が \(60~{\rm cm}^3\) であるので、
\(\begin{split}~~~(x+2){\, \small \times \,}(x-2){\, \small \times \,}1=60\end{split}\)
④ この2次方程式を解く。
⑤ 解が問題に適していることを確認する。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:2次方程式と容積
問題

横の長さが縦の長さより \(5~{\rm cm}\) 長い長方形の紙がある。この紙の四すみから1辺 \(2~{\rm cm}\) の正方形を切り取って、ふたのない箱を作った。
箱の容積が \(132~{\rm cm}^3\) となるとき、もとの長方形の縦の長さと横の長さを求めよ。

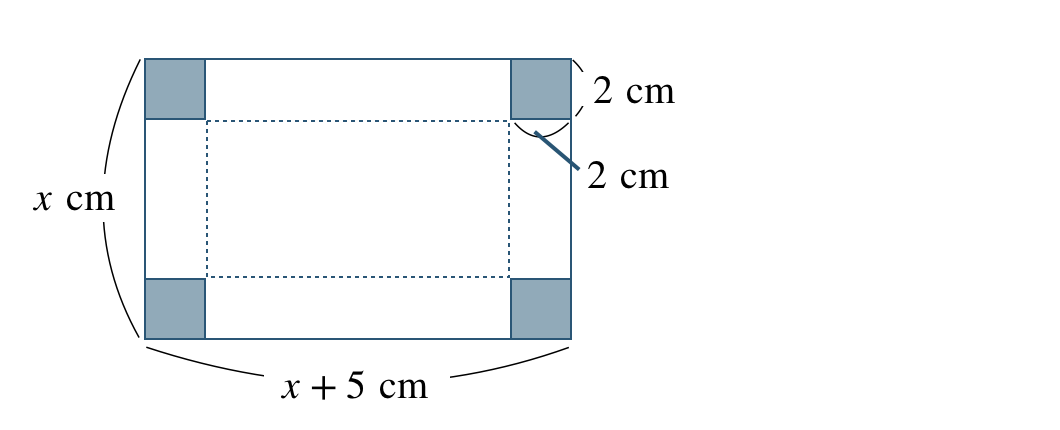
縦の長さを \(x~{\rm cm}\) とすると、横の長さは \(x+5~{\rm cm}\) となる
箱の底面の辺の長さは、
\(\begin{eqnarray}~~~x-2-2&=&x-4~{\rm cm}\\[2pt]~~~x+5-2-2&=&x+1~{\rm cm}\end{eqnarray}\)
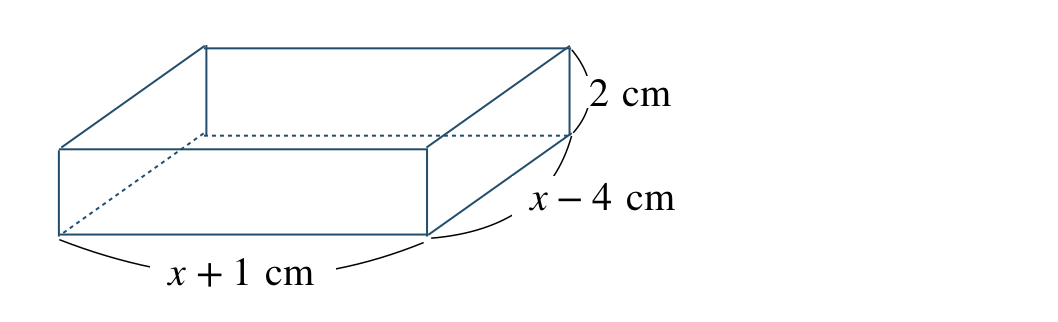
体積が \(132~{\rm cm}^3\) であるので、
\(\begin{eqnarray}~~~(x+1){\, \small \times \,}(x-4){\, \small \times \,}2&=&132\\[2pt]~~~2(x+1)(x-4)&=&132\end{eqnarray}\)
この2次方程式を解くと、
\(\begin{eqnarray}~~~2(x+1)(x-4)&=&132\\[2pt]~~~(x+1)(x-4)&=&66\\[2pt]\hspace{10pt}~~~x^2-3x-4-66&=&0\\[2pt]~~~x^2-3x-70&=&0\\[2pt]~~~(x-10)(x+7)&=&0\\[2pt]~~~x&=&10~,~-7\end{eqnarray}\)
\(x>4\) でなければならないので、
※ 縦の長さは切り取る \(2~{\rm cm}\) の2倍より大きくなければならない。
\(x=-7\) は問題に適していない
\(x=10\) は問題に適している
これより、横の長さは、
\(~~~x+5=10+5=15~{\rm cm}\)
したがって、答えは
縦の長さ \(10~{\rm cm}\)、横の長さ \(15~{\rm cm}\)となる

【問題一覧】中3|2次方程式
このページは「中学数学3 2次方程式」の問題一覧ページとなります。解説の見たい単元名がわからないとき...


