今回の問題は「2次方程式と動く点」です。
\(~\)数研出版 これからの数学3 p.91 問2
\(~\)東京書籍 新しい数学3 p.89 問3
\(~\)啓林館 未来へひろがる数学3 p.84~85 問6
問題

図のような正方形 \({\rm ABCD}\) がある。
点 \({\rm P}\) は点 \({\rm A}\) を出発して辺 \({\rm AB}\) を秒速 \(2~{\rm cm}\) で点 \({\rm B}\) まで動く。また、点 \({\rm Q}\) は点 \({\rm P}\) と同時に点 \({\rm B}\) を出発して辺 \({\rm BC}\) を秒速 \(1~{\rm cm}\) で点 \({\rm C}\) まで動く。このとき、\(\triangle {\rm PBQ}\) の面積が \(5~{\rm cm}^2\) になるのは点 \({\rm P~,~Q}\) が出発して何秒後か答えよ。

Point:2次方程式と動く点
① \(x\) 秒後の点Pと点Qを図にかく。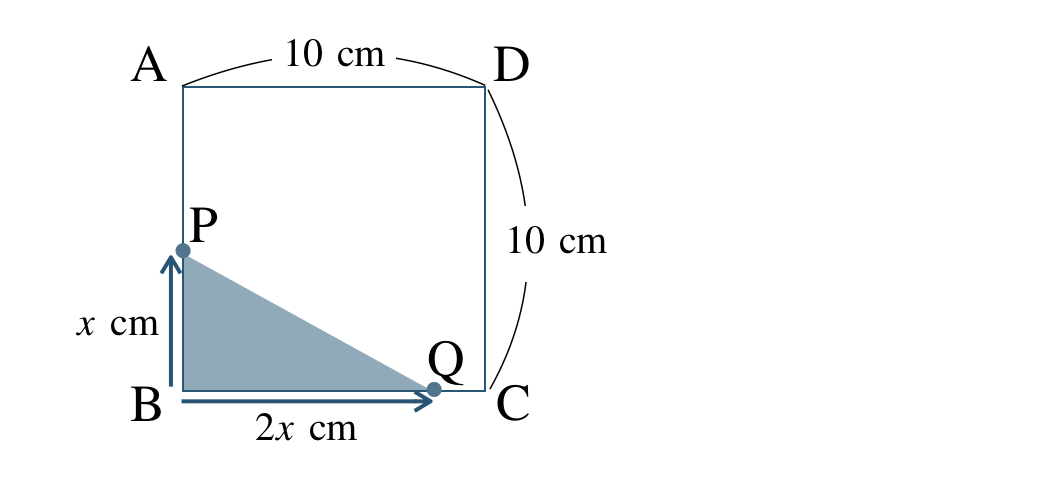
△PBQの面積が \(9~{\rm cm}^2\) であるので、
\(\begin{split}~~~ \frac{\,1\,}{\,2\,}{\, \small \times \,} x{\, \small \times \,} 2x=9\end{split}\)
③ 2次方程式を解く。
④ 解が問題に適していることを確認する。
1辺 \(10~{\rm cm}\) の正方形ABCDを点Pは点B→点Aを毎秒 \(1~{\rm cm}\)、点Qは点B→点Cを毎秒 \(2~{\rm cm}\) で進むとき、△PBQの面積が \(9~{\rm cm}^2\) となるのは、
① \(x\) 秒後の点Pと点Qを図にかく。

② 面積の条件から、2次方程式を立てる。
△PBQの面積が \(9~{\rm cm}^2\) であるので、
\(\begin{split}~~~ \frac{\,1\,}{\,2\,}{\, \small \times \,} x{\, \small \times \,} 2x=9\end{split}\)
③ 2次方程式を解く。
④ 解が問題に適していることを確認する。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
次のページ「解法のPointと問題解説」


