問題:関数y=ax²と変域
問題
\({\small (1)}~\)関数 \(y=x^2\) について、\(x\) の変域が
次のとき、\(y\) の増減と \(y\) の変域を求めよ。
① \(\begin{split}1≦x≦2\end{split}\)
② \(\begin{split}-3≦x≦1\end{split}\)
\({\small (2)}~\)関数 \(\begin{split}y=-{\frac{\,1\,}{\,2\,}}x^2\end{split}\) について、\(x\) の変域が
次のとき、\(y\) の増減と \(y\) の変域を求めよ。
① \(\begin{split}-4≦x≦-2\end{split}\)
② \(\begin{split}-1≦x≦4\end{split}\)
次の問いに答えよ。
\({\small (1)}~\)関数 \(y=x^2\) について、\(x\) の変域が
次のとき、\(y\) の増減と \(y\) の変域を求めよ。
① \(\begin{split}1≦x≦2\end{split}\)
② \(\begin{split}-3≦x≦1\end{split}\)
\({\small (2)}~\)関数 \(\begin{split}y=-{\frac{\,1\,}{\,2\,}}x^2\end{split}\) について、\(x\) の変域が
次のとき、\(y\) の増減と \(y\) の変域を求めよ。
① \(\begin{split}-4≦x≦-2\end{split}\)
② \(\begin{split}-1≦x≦4\end{split}\)
解法のPoint
Point:関数y=ax²の増減
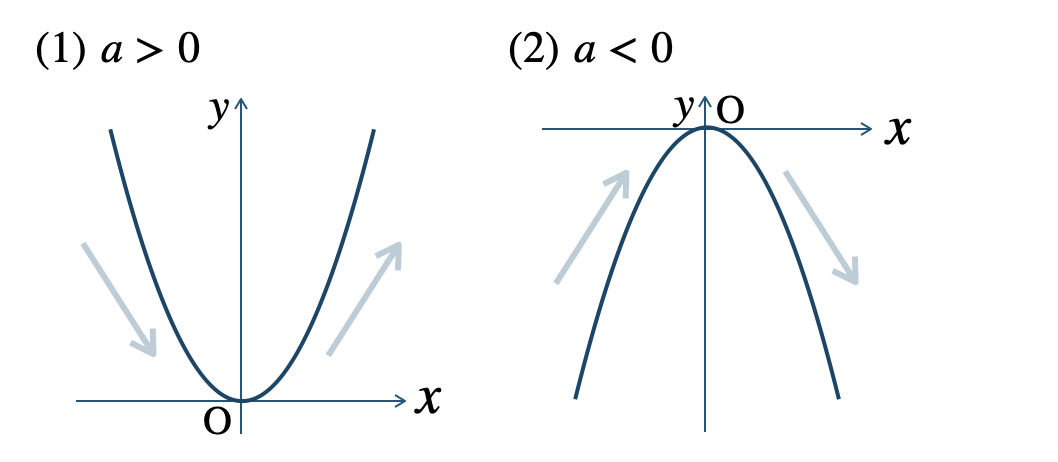
\(x< 0\) で、\(x\) が増加すると、\(y\) は減少する
\(x> 0\) で、\(x\) が増加すると、\(y\) は増加する
\(x=0\) のとき、\(y=0\) となり、最小値となる
また、\(x=0\) の前後で減少から増加に変わる
\({\small (2)}~\)\(a< 0\) のとき、
\(x< 0\) で、\(x\) が増加すると、\(y\) は増加する
\(x> 0\) で、\(x\) が増加すると、\(y\) は減少する
\(x=0\) のとき、\(y=0\) となり、最大値となる
また、\(x=0\) の前後で増加から減少に変わる
関数 \(y=ax^2\) の値の増減は、

\({\small (1)}~\)\(a> 0\) のとき、
\(x< 0\) で、\(x\) が増加すると、\(y\) は減少する
\(x> 0\) で、\(x\) が増加すると、\(y\) は増加する
\(x=0\) のとき、\(y=0\) となり、最小値となる
また、\(x=0\) の前後で減少から増加に変わる
\({\small (2)}~\)\(a< 0\) のとき、
\(x< 0\) で、\(x\) が増加すると、\(y\) は増加する
\(x> 0\) で、\(x\) が増加すると、\(y\) は減少する
\(x=0\) のとき、\(y=0\) となり、最大値となる
また、\(x=0\) の前後で増加から減少に変わる
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
Point:関数y=ax²と変域
関数 \(\begin{split}y=\frac{\,1\,}{\,2\,}x^2~~(-2≦x≦4)\end{split}\) の \(y\) の値の
増減の調べ方と \(y\) の変域の求め方は、
① 定義域の範囲でグラフをかく。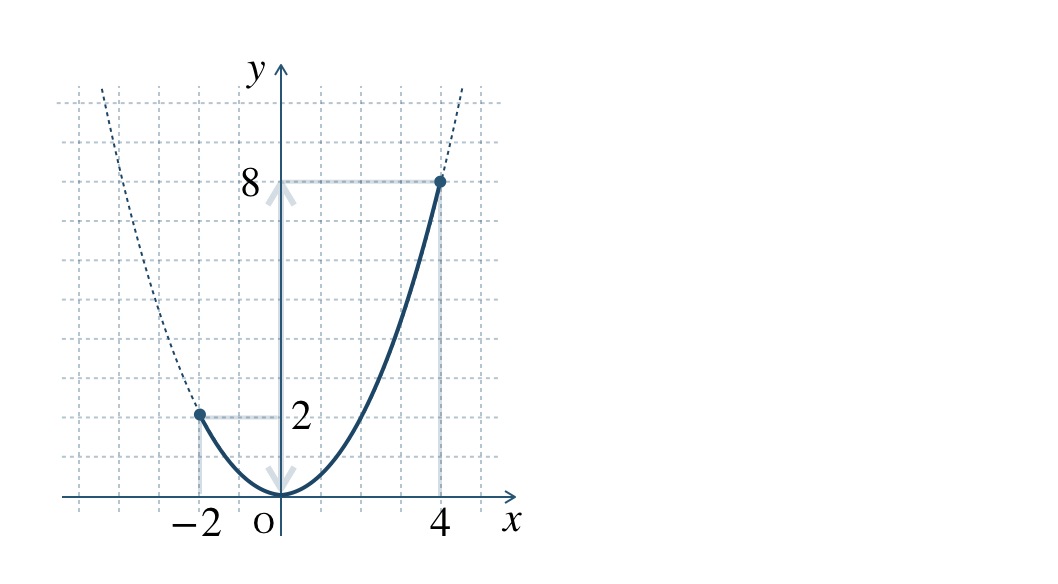
\(-2≦x≦0\) のとき、
\(y\) は \(2\) から \(0\) まで減少する
\(0≦x≦4\) のとき、
\(y\) は \(0\) から \(8\) まで増加する
\(x=0\) のとき、\(y=0\) で最小値となる
③ 最大値と最小値から \(y\) の変域を求める。
\(y\) の最大値は \(8\)、最小値は \(0\) より、
\(y\) の変域は、\(0≦y≦8\) となる
関数 \(\begin{split}y=\frac{\,1\,}{\,2\,}x^2~~(-2≦x≦4)\end{split}\) の \(y\) の値の
増減の調べ方と \(y\) の変域の求め方は、
① 定義域の範囲でグラフをかく。

② グラフから増減を読み取る。
\(-2≦x≦0\) のとき、
\(y\) は \(2\) から \(0\) まで減少する
\(0≦x≦4\) のとき、
\(y\) は \(0\) から \(8\) まで増加する
\(x=0\) のとき、\(y=0\) で最小値となる
③ 最大値と最小値から \(y\) の変域を求める。
\(y\) の最大値は \(8\)、最小値は \(0\) より、
\(y\) の変域は、\(0≦y≦8\) となる
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:関数y=ax²と変域
問題解説(1)
問題
\({\small (1)}~\)関数 \(y=x^2\) について、\(x\) の変域が
次のとき、\(y\) の増減と \(y\) の変域を求めよ。
① \(\begin{split}1≦x≦2\end{split}\)
② \(\begin{split}-3≦x≦1\end{split}\)
次の問いに答えよ。
\({\small (1)}~\)関数 \(y=x^2\) について、\(x\) の変域が
次のとき、\(y\) の増減と \(y\) の変域を求めよ。
① \(\begin{split}1≦x≦2\end{split}\)
② \(\begin{split}-3≦x≦1\end{split}\)
① \(\begin{split}1≦x≦2\end{split}\)
\(x=1\) のとき、\(\begin{split}y=1^2=1\end{split}\)
\(x=2\) のとき、\(\begin{split}y=2^2=4\end{split}\)
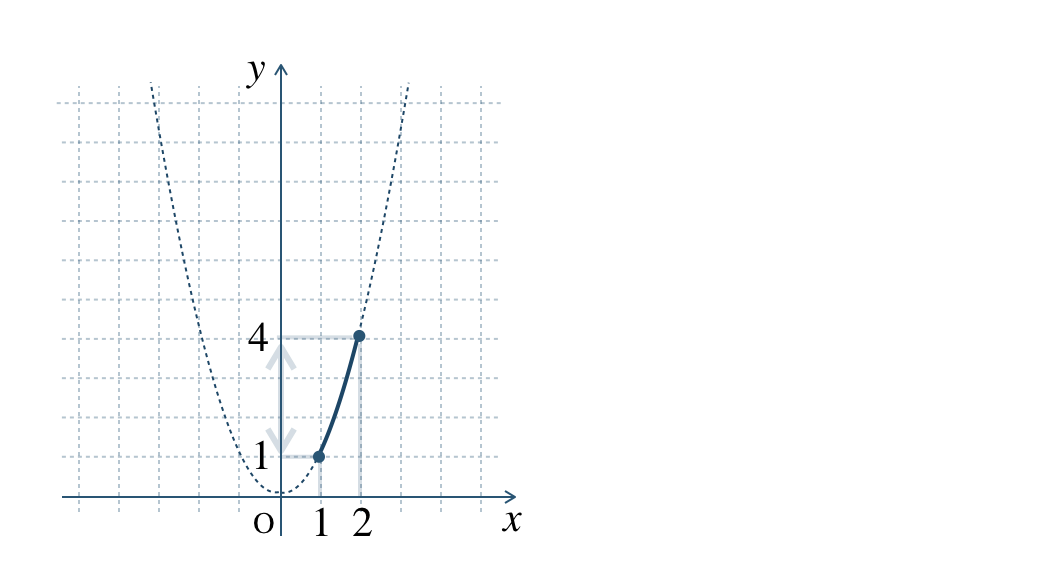
グラフより、\(1≦x≦2\) のとき、
\(y\) は \(1\) から \(4\) まで増加する
したがって、\(y\) の変域は、\(\begin{split}1≦y≦4\end{split}\) となる
② \(\begin{split}-3≦x≦1\end{split}\)
\(x=-3\) のとき、\(\begin{split}y=(-3)^2=9\end{split}\)
\(x=1\) のとき、\(\begin{split}y=1^2=1\end{split}\)
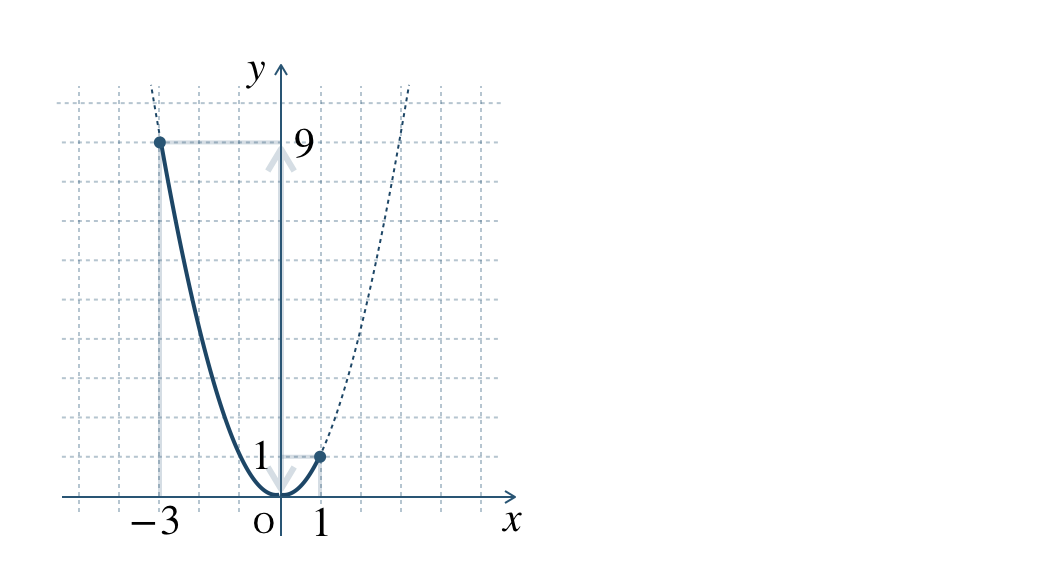
グラフより、\(-3≦x≦0\) のとき、
\(y\) は \(9\) から \(0\) まで減少する
グラフより、\(0≦x≦1\) のとき、
\(y\) は \(0\) から \(1\) まで増加する
\(x=0\) のとき、\(y=0\) で最小値となる
したがって、\(y\) の変域は、\(\begin{split}0≦y≦9\end{split}\) となる
問題解説(2)
問題
\({\small (2)}~\)関数 \(\begin{split}y=-{\frac{\,1\,}{\,2\,}}x^2\end{split}\) について、\(x\) の変域が
次のとき、\(y\) の増減と \(y\) の変域を求めよ。
① \(\begin{split}-4≦x≦-2\end{split}\)
② \(\begin{split}-1≦x≦4\end{split}\)
次の問いに答えよ。
\({\small (2)}~\)関数 \(\begin{split}y=-{\frac{\,1\,}{\,2\,}}x^2\end{split}\) について、\(x\) の変域が
次のとき、\(y\) の増減と \(y\) の変域を求めよ。
① \(\begin{split}-4≦x≦-2\end{split}\)
② \(\begin{split}-1≦x≦4\end{split}\)
① \(\begin{split}-4≦x≦-2\end{split}\)
\(x=-4\) のとき、
\(\begin{split}~~~y=-\frac{\,1\,}{\,2\,}{\, \small \times \,}(-4)^2=-\frac{\,1\,}{\,2\,}{\, \small \times \,}16=-8\end{split}\)
\(x=-2\) のとき、
\(\begin{split}~~~y=-\frac{\,1\,}{\,2\,}{\, \small \times \,}(-2)^2=-\frac{\,1\,}{\,2\,}{\, \small \times \,}4=-2\end{split}\)
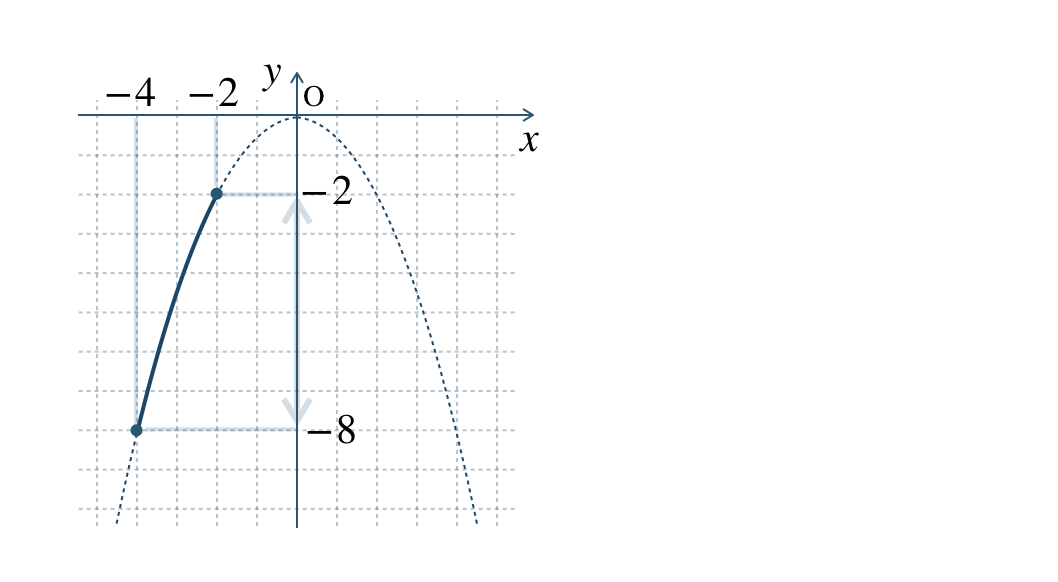
グラフより、\(-4≦x≦-2\) のとき、
\(y\) は \(-8\) から \(-2\) まで増加する
したがって、\(y\) の変域は、\(\begin{split}-8≦y≦-2\end{split}\) となる
② \(\begin{split}-1≦x≦4\end{split}\)
\(x=-1\) のとき、
\(\begin{split}~~~y=-\frac{\,1\,}{\,2\,}{\, \small \times \,}(-1)^2=-\frac{\,1\,}{\,2\,}{\, \small \times \,}1=-\frac{\,1\,}{\,2\,}\end{split}\)
\(x=4\) のとき、
\(\begin{split}~~~y=-\frac{\,1\,}{\,2\,}{\, \small \times \,}4^2=-\frac{\,1\,}{\,2\,}{\, \small \times \,}16=-8\end{split}\)
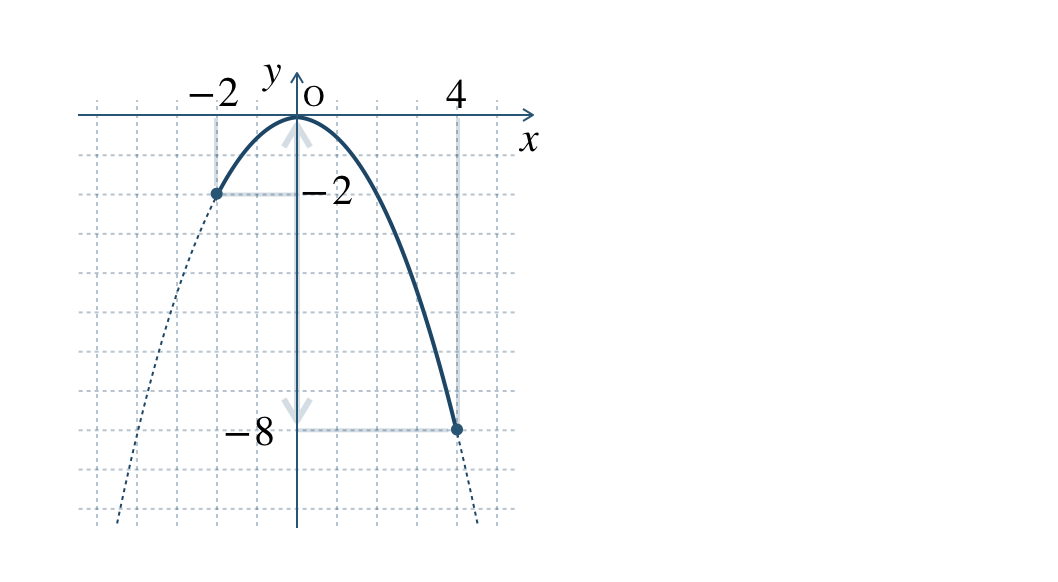
グラフより、\(-1≦x≦0\) のとき、
\(y\) は \(\begin{split}{\frac{\,1\,}{\,2\,}}\end{split}\) から \(0\) まで増加する
グラフより、\(0≦x≦4\) のとき、
\(y\) は \(0\) から \(-8\) まで減少する
\(x=0\) のとき、\(y=0\) で最大値となる
したがって、\(y\) の変域は、\(\begin{split}-8≦y≦0\end{split}\) となる

【問題一覧】中3|関数y=ax²
このページは「中学数学3 関数y=ax²」の問題一覧ページとなります。解説の見たい単元名がわからない...


