今回の問題は「関数y=ax²のグラフ」です。
\(~\)数研出版 これからの数学1 p.106~110 問3~6
\(~\)東京書籍 新しい数学1 p.103~106 問2~6
\(~\)啓林館 未来へひろがる数学1 p.98~101 問3~4
問題
\({\small (1)}~\)\(y=x^2\) のグラフを参考にして、\(y=2x^2\) のグラフをかけ。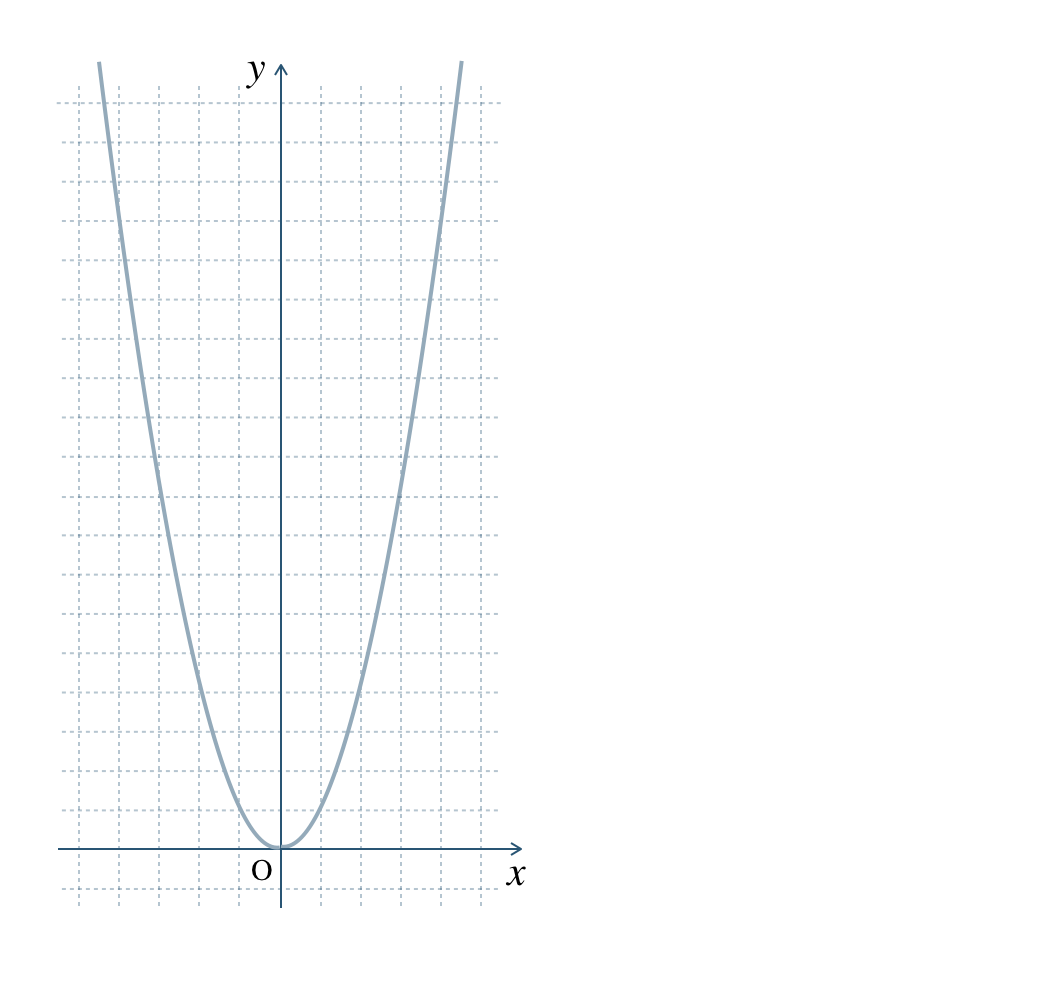
\(\begin{split}y=-{\frac{\,1\,}{\,2\,}}x^2\end{split}\) のグラフをかけ。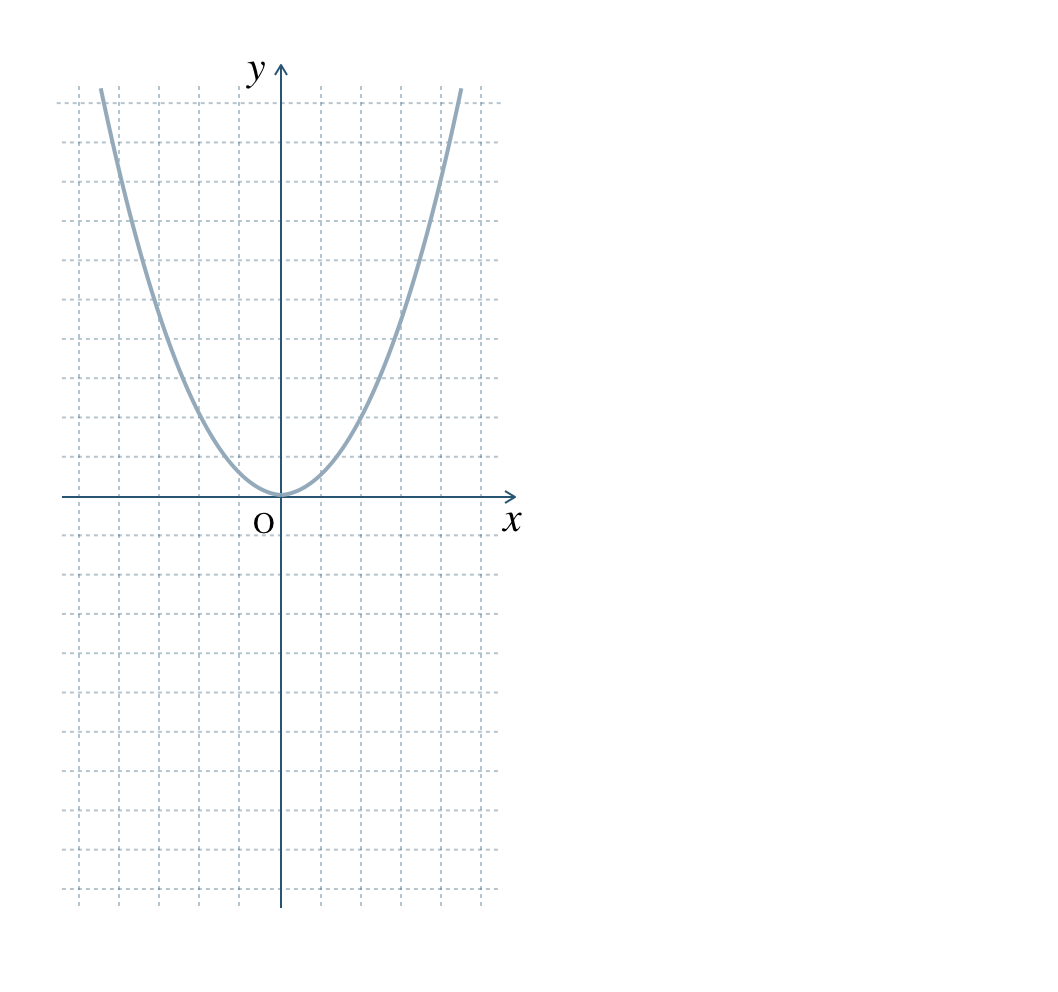
\(\begin{split}~~~y=x^2~,~y=3x^2~,~y=-2x^2\end{split}\)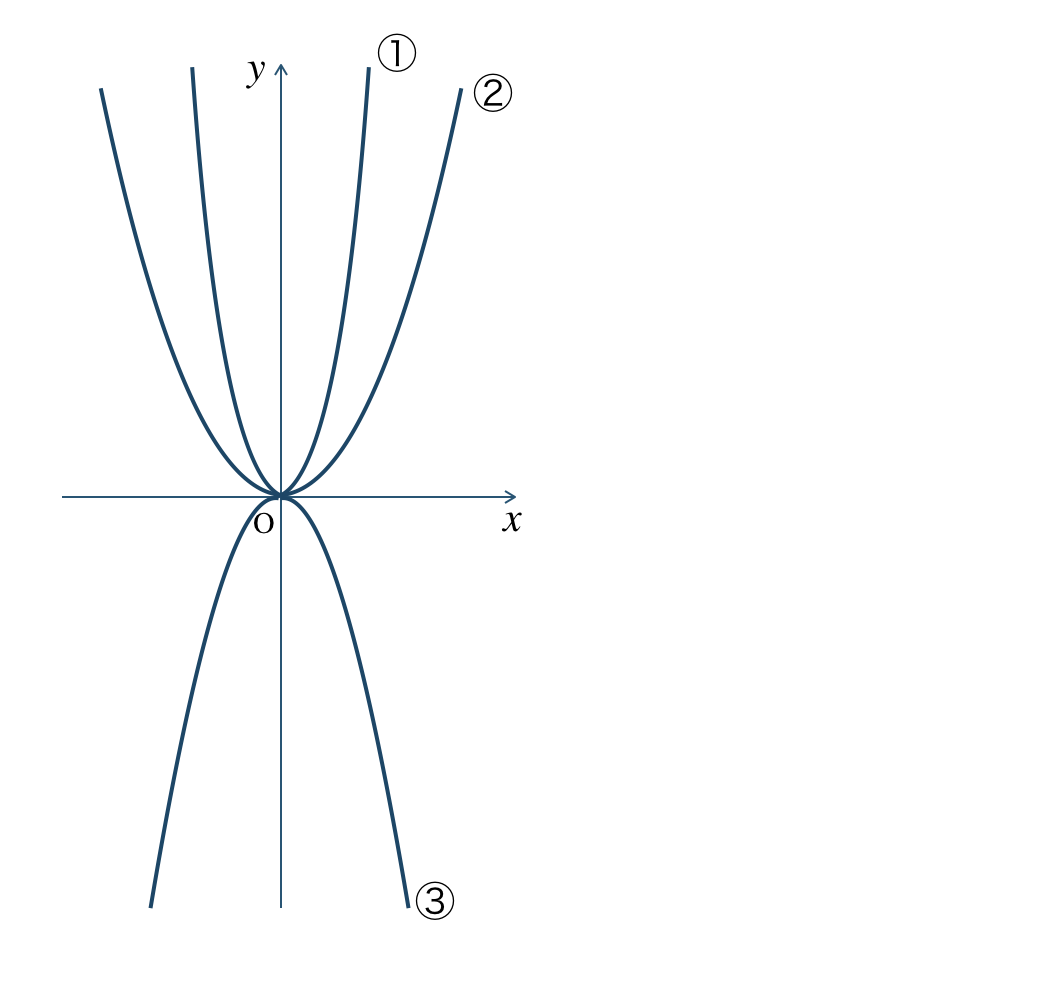
次の問いに答えよ。
\({\small (1)}~\)\(y=x^2\) のグラフを参考にして、\(y=2x^2\) のグラフをかけ。

\({\small (2)}~\)\(\begin{split}y={\frac{\,1\,}{\,2\,}}x^2\end{split}\) のグラフを参考にして、
\(\begin{split}y=-{\frac{\,1\,}{\,2\,}}x^2\end{split}\) のグラフをかけ。

\({\small (3)}~\)次の図の①〜③のグラフは、次のどの関数となるか選べ。
\(\begin{split}~~~y=x^2~,~y=3x^2~,~y=-2x^2\end{split}\)

Point:関数y=ax²のグラフ
原点を通り、\(y\) 軸に対称な「放物線」となる。
\(y\) 軸を「対称の軸」といい、この軸と放物線の交点を「頂点」という。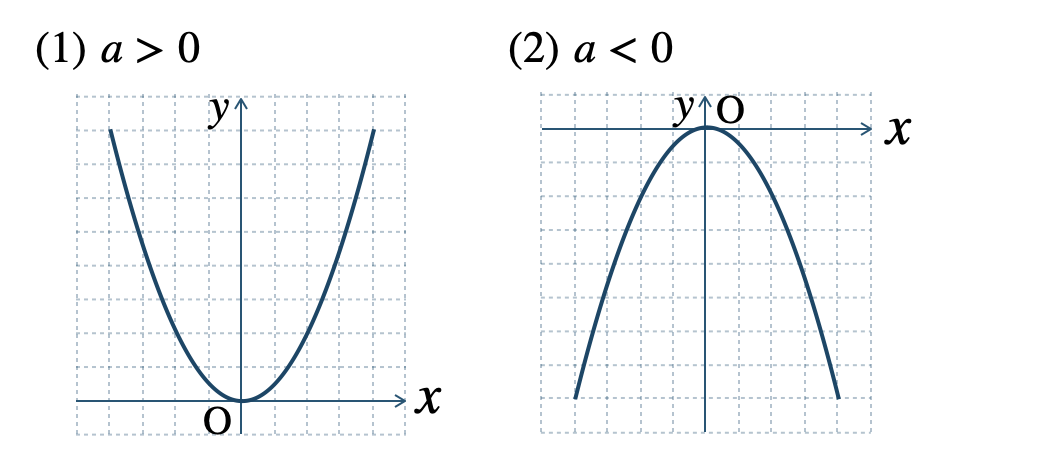
\({\small (2)}~\)\(a< 0\) のとき、下に開いたグラフ
\(a\) の絶対値が大きくなるほど、グラフの開きぐあいが小さくなる。
※ \(y=ax^2\) のグラフと \(y=-ax^2\) のグラフは \(x\) 軸で対称である。
関数 \(y=ax^2\) のグラフは、
原点を通り、\(y\) 軸に対称な「放物線」となる。
\(y\) 軸を「対称の軸」といい、この軸と放物線の交点を「頂点」という。

\({\small (1)}~\)\(a> 0\) のとき、上に開いたグラフ
\({\small (2)}~\)\(a< 0\) のとき、下に開いたグラフ
\(a\) の絶対値が大きくなるほど、グラフの開きぐあいが小さくなる。
※ \(y=ax^2\) のグラフと \(y=-ax^2\) のグラフは \(x\) 軸で対称である。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
次のページ「解法のPointと問題解説」


