問題:相似の位置
次の問いに答えよ。
\({\small (1)}~\)次の図に、点 \({\rm O}\) を相似の中心として、\(\triangle {\rm ABC}\) を \(2\) 倍に拡大した \(\triangle {\rm A’B’C’}\) をかけ。
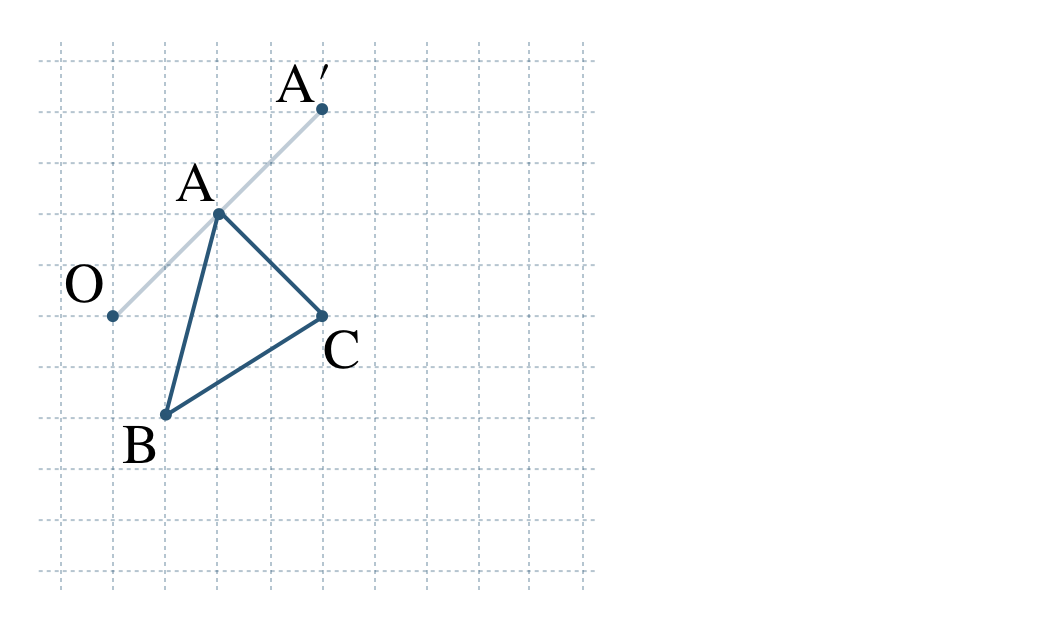
\({\small (2)}~\)次の図に、点 \({\rm O}\) を相似の中心として、\(\triangle {\rm ABC}\) を \(3\) 倍に拡大した \(\triangle {\rm A’B’C’}\) をかけ。
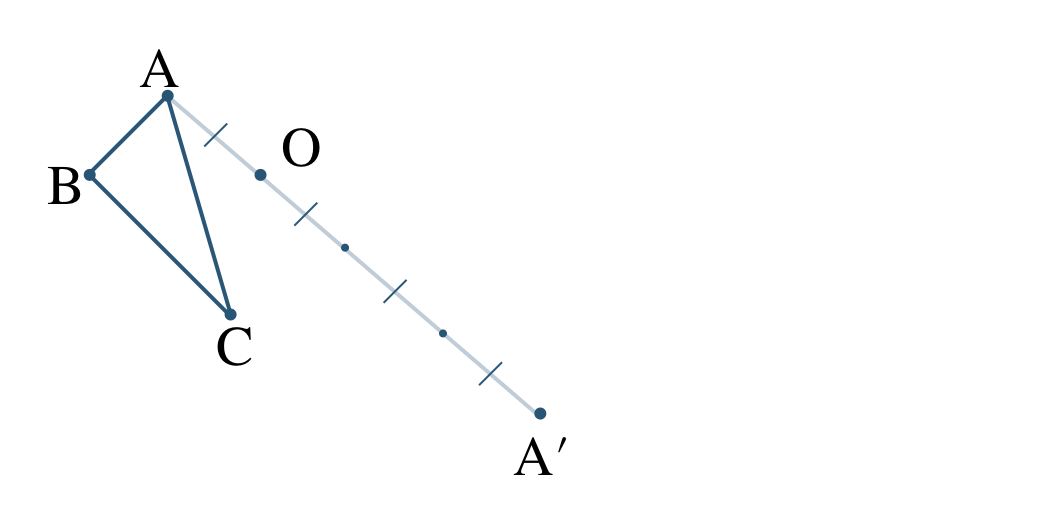
\({\small (3)}~\)次の図に、点 \({\rm O}\) を相似の中心として、四角形 \( {\rm ABCD}\) を \(\begin{split} \frac{\,1\,}{\,2\,}\end{split}\) 倍に縮小した四角形 \( {\rm A’B’C’D’}\) をかけ。
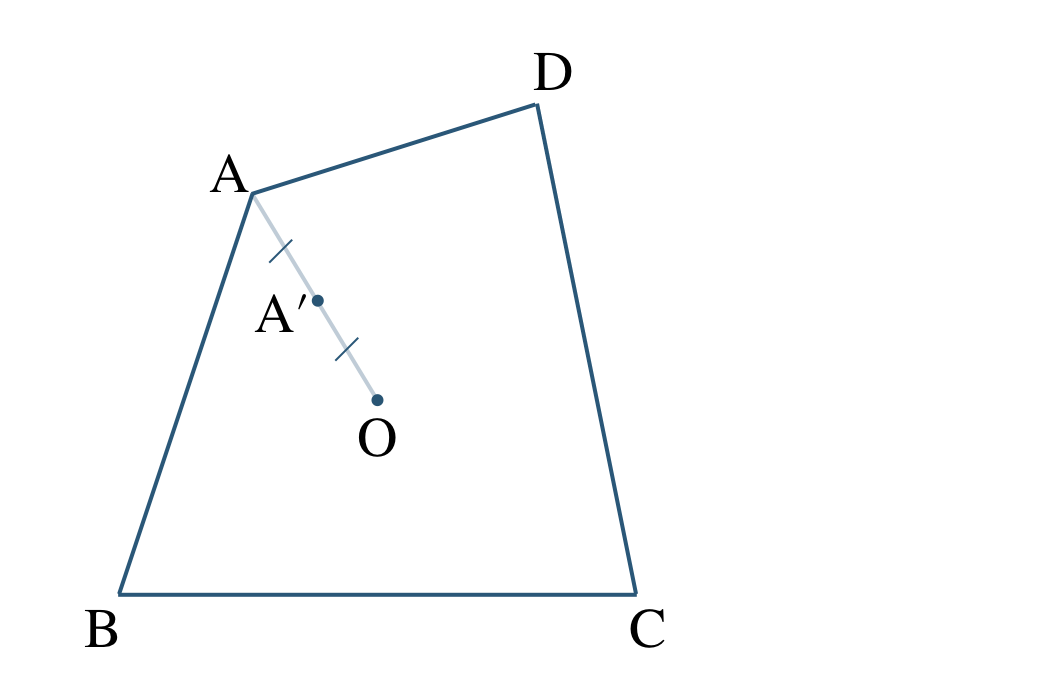
解法のPoint
■ 相似の位置
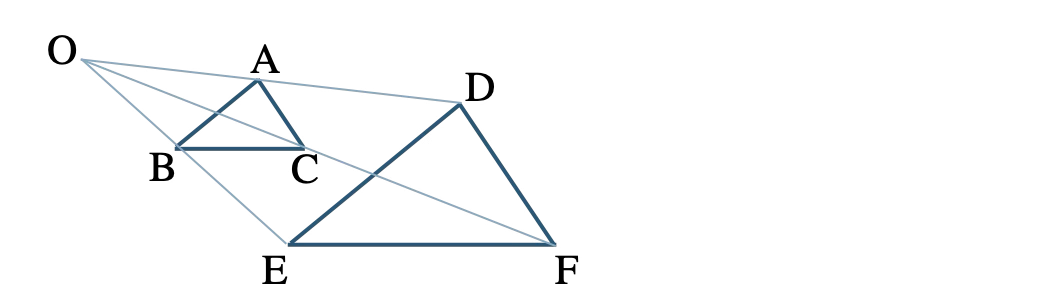
\(\triangle {\rm ABC}\) と \(\triangle {\rm DEF}\) のように、
2つの図形の対応する頂点をむすんだ直線が1点 \({\rm O}\) で交わり、点 \({\rm O}\) と対応するまでの距離の比がすべて等しいとき、
\({\rm OA:OD=OB:OE=OC:OF}\)
この2つの図形は「相似」であり、「相似の位置にある」といい、点 \({\rm O}\) を「相似の中心」という。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:相似の位置
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)次の図に、点 \({\rm O}\) を相似の中心として、\(\triangle {\rm ABC}\) を \(2\) 倍に拡大した \(\triangle {\rm A’B’C’}\) をかけ。

\(2\) 倍に拡大した三角形より、相似の中心が \({\rm O}\) となるので、
点 \({\rm B}\) は点 \({\rm O}\) から右に \(1\)、下に \(2\) の位置にあるので、点 \({\rm B’}\) は \(2\) 倍した右に \(2\)、下に \(4\) の位置にある
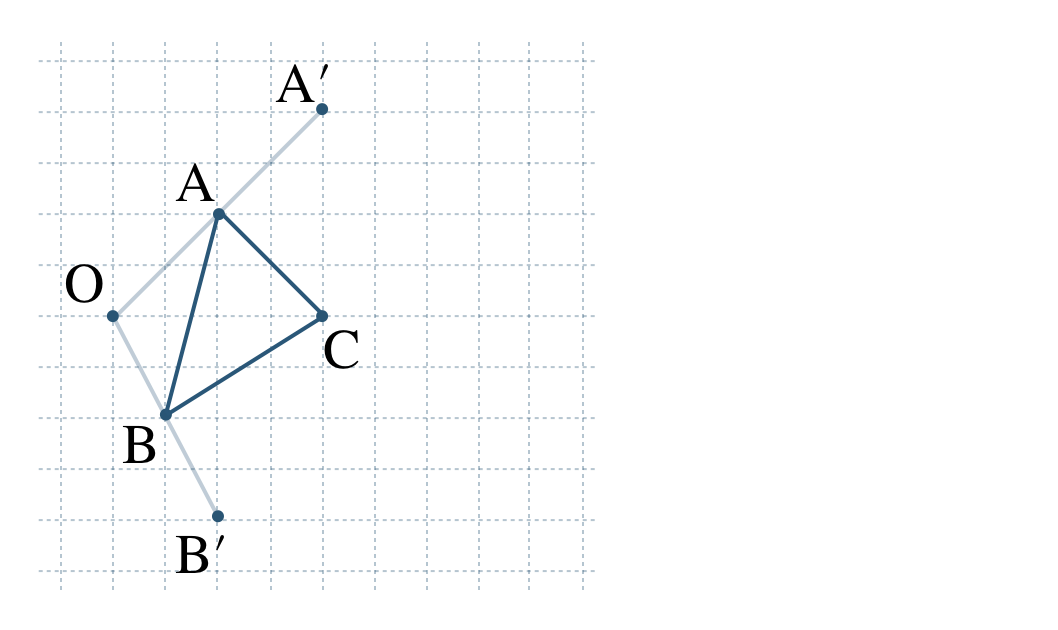
点 \({\rm C}\) は点 \({\rm O}\) から右に \(4\) の位置にあるので、点 \({\rm C’}\) は \(2\) 倍した右に \(8\) の位置にある
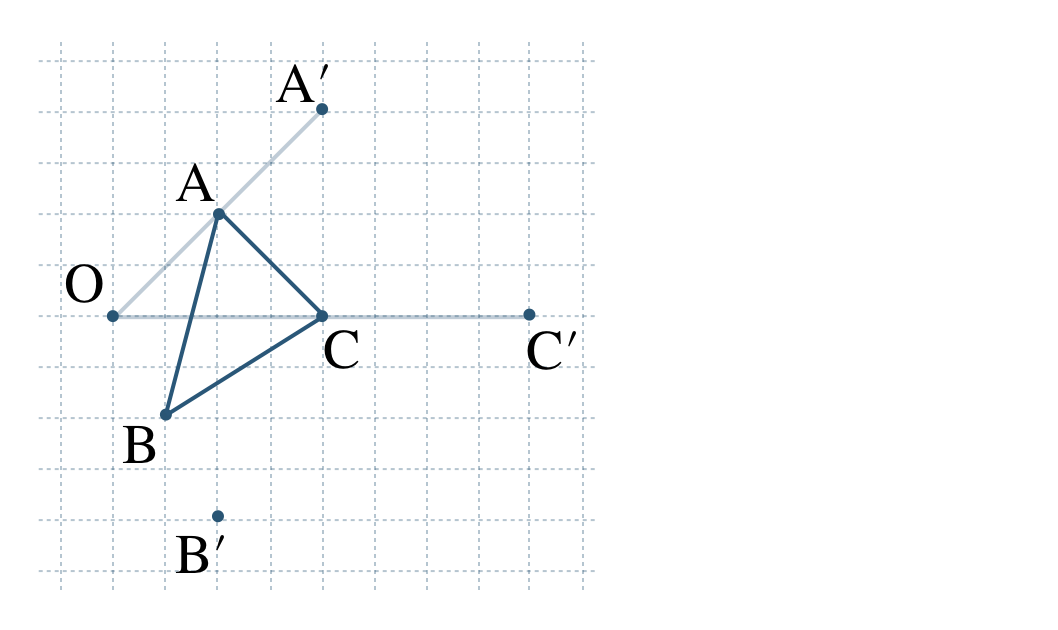
これより、3つの点 \({\rm A’~,~B’~,~C’}\) をむすぶと、\(\triangle {\rm A’B’C’}\) となる
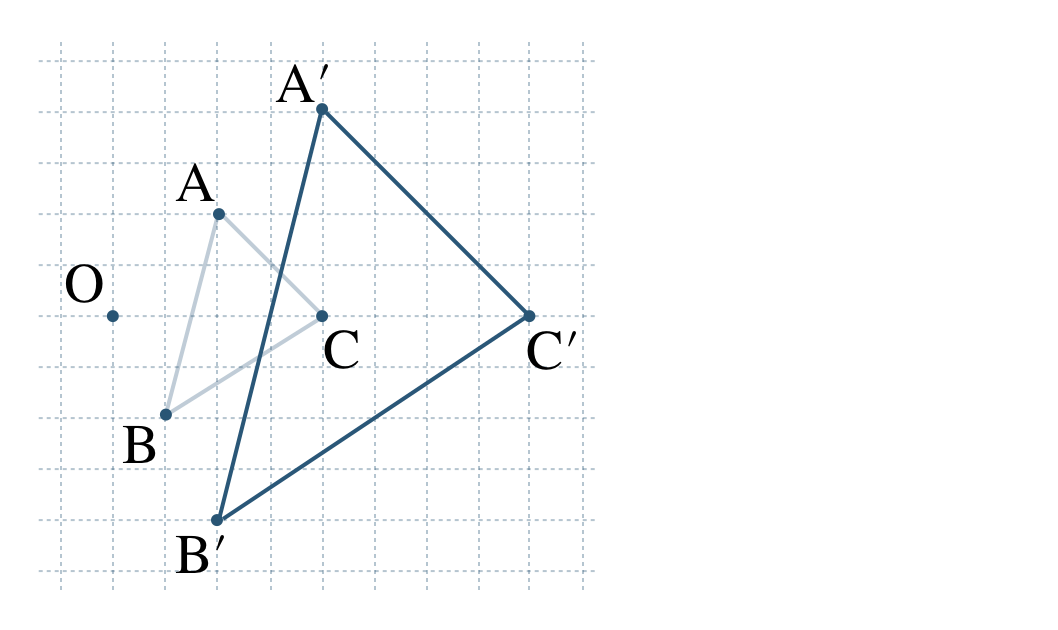
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)次の図に、点 \({\rm O}\) を相似の中心として、\(\triangle {\rm ABC}\) を \(3\) 倍に拡大した \(\triangle {\rm A’B’C’}\) をかけ。

\(3\) 倍に拡大した三角形より、相似の中心が \({\rm O}\) となるので、
半直線 \({\rm BO}\) をひき、\({\rm OB’=3OB}\) となるように点 \({\rm B’}\) をとると、
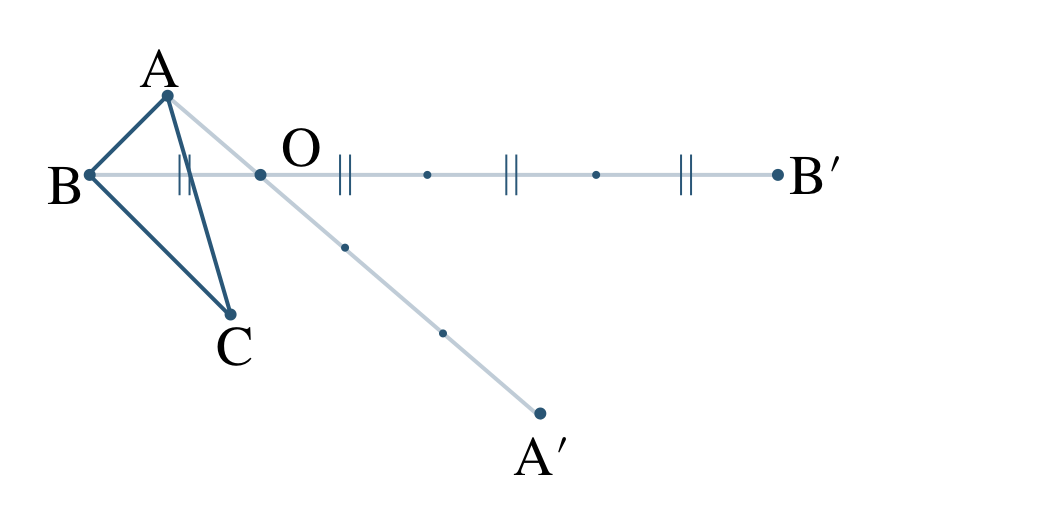
半直線 \({\rm CO}\) をひき、\({\rm OC’=3OC}\) となるように点 \({\rm C’}\) をとると、
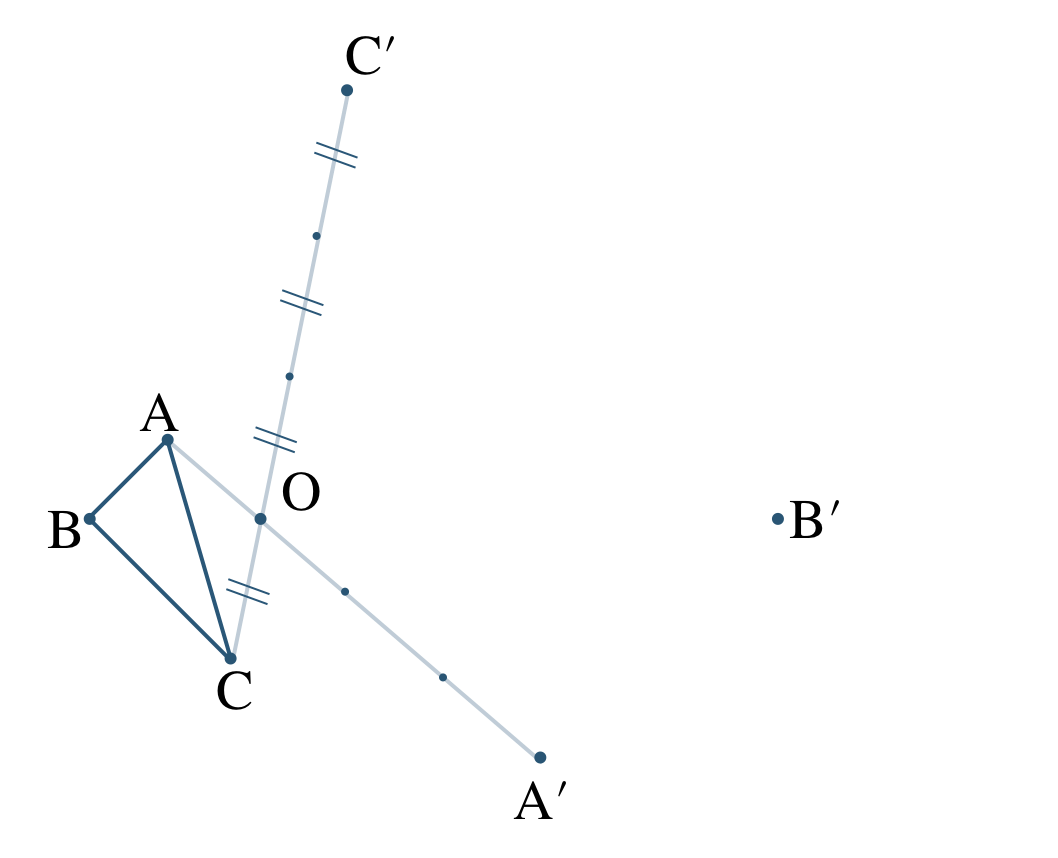
これより、3つの点 \({\rm A’~,~B’~,~C’}\) をむすぶと、\(\triangle {\rm A’B’C’}\) となる

問題解説(3)
次の問いに答えよ。
\({\small (3)}~\)次の図に、点 \({\rm O}\) を相似の中心として、四角形 \( {\rm ABCD}\) を \(\begin{split} \frac{\,1\,}{\,2\,}\end{split}\) 倍に縮小した四角形 \( {\rm A’B’C’D’}\) をかけ。

\(\begin{split} \frac{\,1\,}{\,2\,}\end{split}\) 倍に縮小した三角形より、相似の中心が \({\rm O}\) となるので、
線分 \({\rm OB}\) をひき、\(\begin{split}{\rm OB’={\frac{\,1\,}{\,2\,}}OB}\end{split}\) となるように点 \({\rm B’}\) をとると、
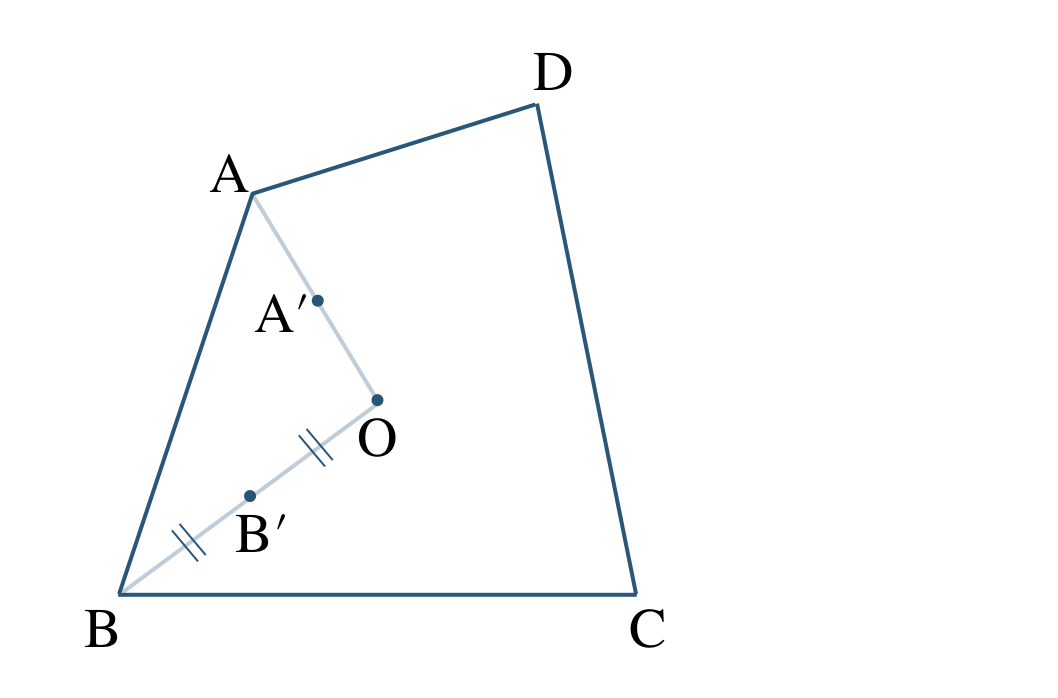
線分 \({\rm OC}\) をひき、\(\begin{split}{\rm OC’={\frac{\,1\,}{\,2\,}}OC}\end{split}\) となるように点 \({\rm C’}\) をとると、
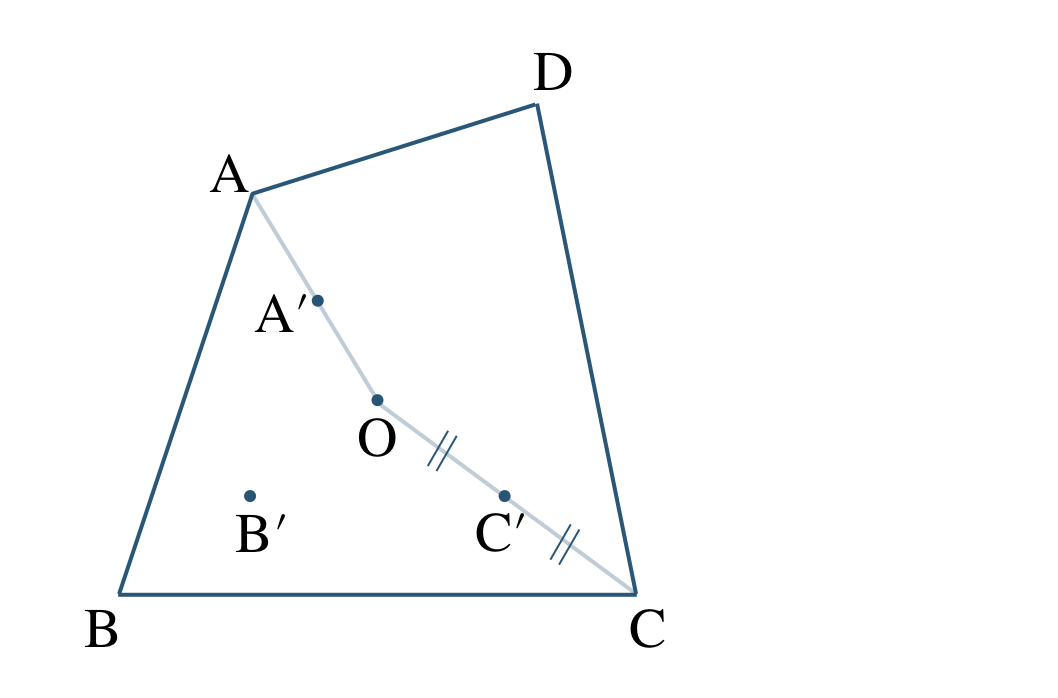
線分 \({\rm OD}\) をひき、\(\begin{split}{\rm OD’={\frac{\,1\,}{\,2\,}}OD}\end{split}\) となるように点 \({\rm D’}\) をとると、
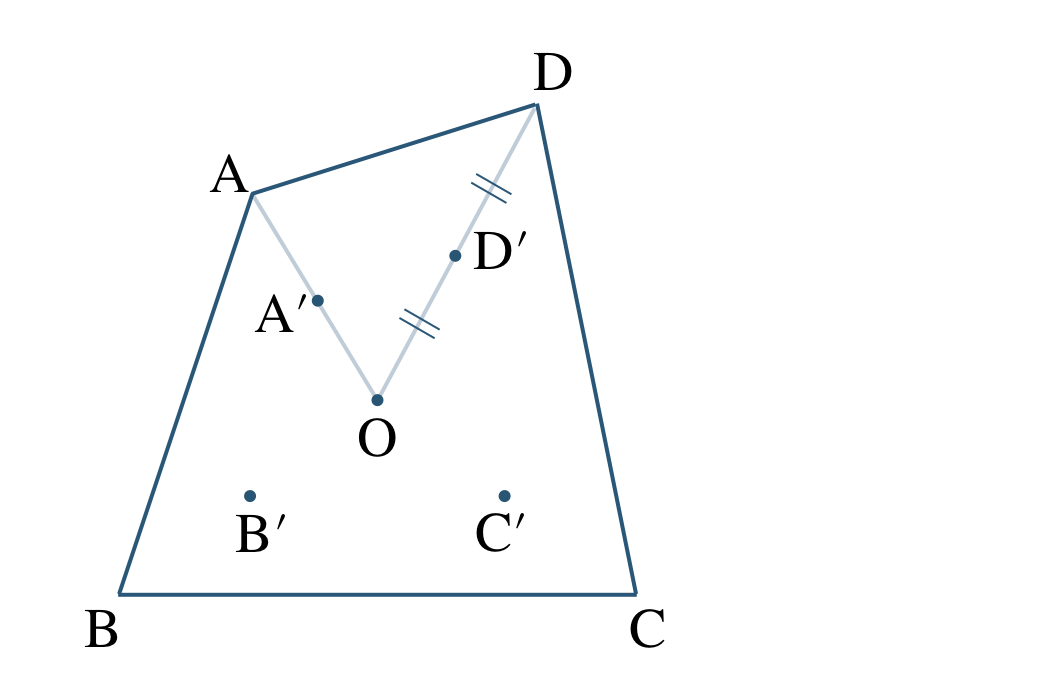
これより、4つの点 \({\rm A’~,~B’~,~C’~,~D’}\) をむすぶと、四角形 \( {\rm A’B’C’D’}\) となる




