相似な三角形の解法
1つの図形から、相似な2つの三角形を見つける方法は、
① 相似になりそうな2つの三角形を見つける。
② 等しい角を見つける。
共通している角、対頂角、平行線の同位角、
平行線の錯角など。
③ 等しい比の辺の組を見つける。
④ 相似条件を考えて、向きをそろえてかく。
\({\small (1)}~\)3組の辺の比がそれぞれ等しい
\({\small (2)}~\)2組の辺の比とその間の角がそれぞれ等しい
\({\small (3)}~\)2組の角がそれぞれ等しい
⑤ 対応する頂点を確認して、相似の記号 \(\unicode{x223D}\) を使って表す。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:相似な三角形
問題解説(1)
次の図において、相似な三角形を見つけて、記号を使って表せ。また、そのときの相似条件を答えよ。
\({\small (1)}~\)
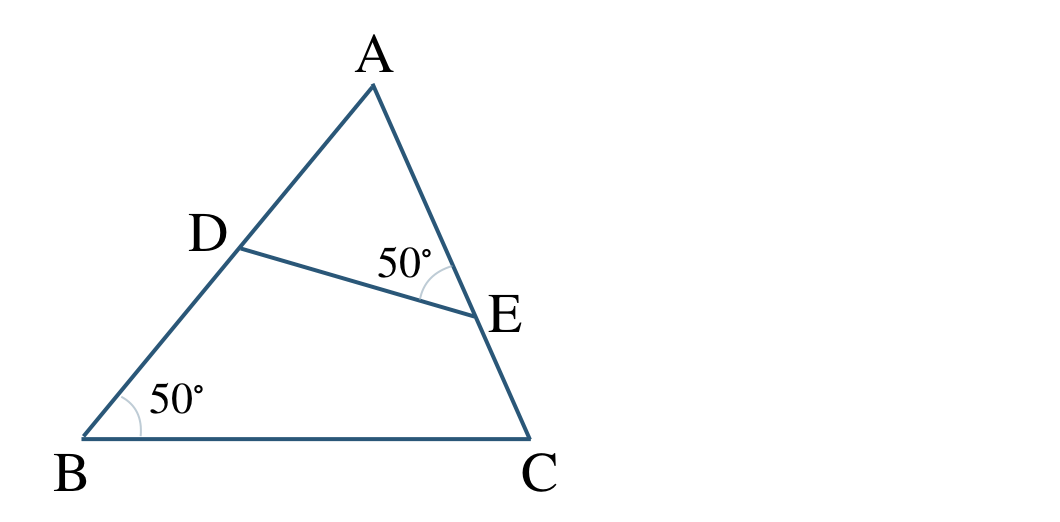
\(\angle {\rm A}\) が共通している角より、
\(\angle{\rm BAC}=\angle{\rm EAD}\)
これより、\(\triangle {\rm ABC}\) と \(\triangle {\rm AED}\) の向きをそろえてかくと、

したがって、
\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm AED}\)
相似条件は、
2組の角がそれぞれ等しい
となる
問題解説(2)
次の図において、相似な三角形を見つけて、記号を使って表せ。また、そのときの相似条件を答えよ。
\({\small (2)}~\)
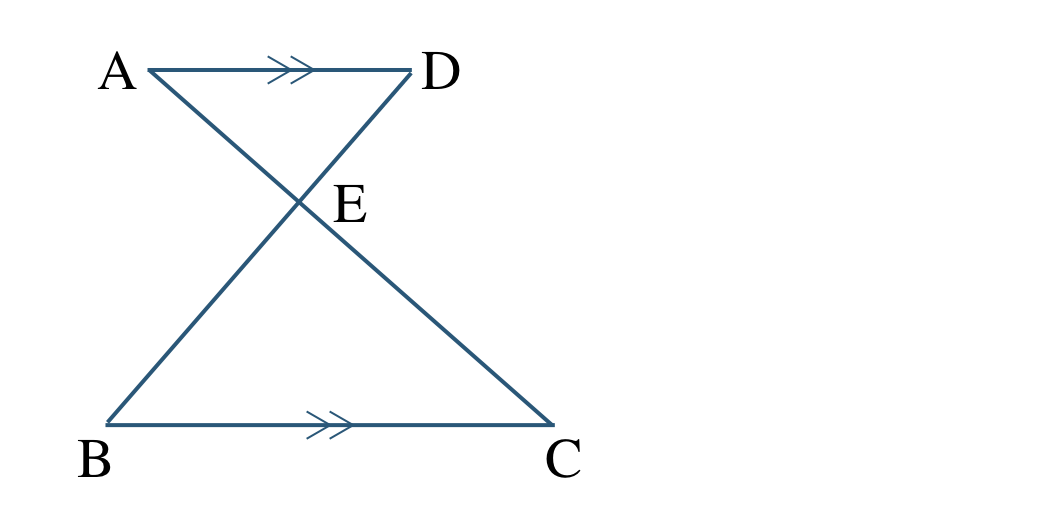
\({\rm AD\,//\,BC}\) より、錯角が等しいので、
\(\angle{\rm DAE}=\angle{\rm BCE}\)
対頂角が等しいので、
\(\angle{\rm AED}=\angle{\rm CEB}\)
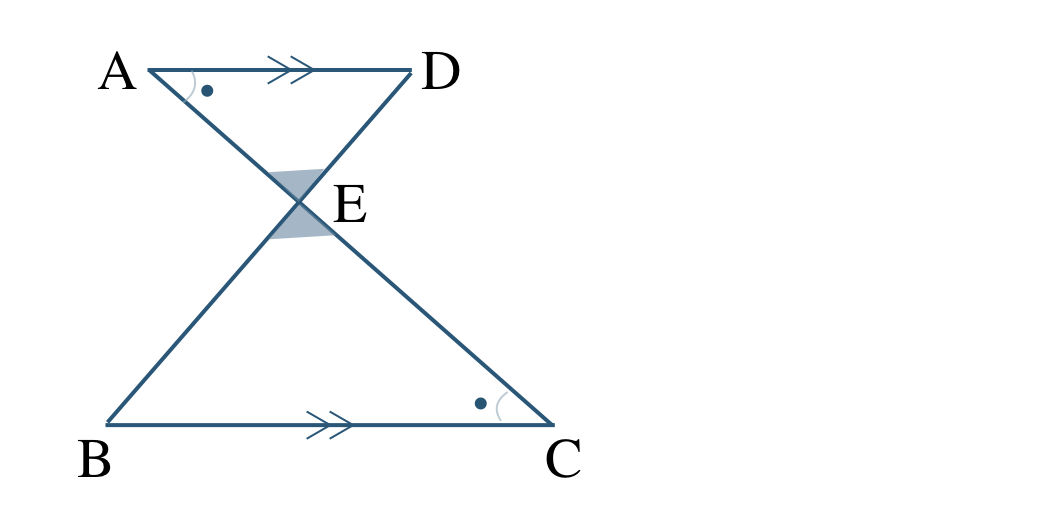
これより、\(\triangle {\rm AED}\) と \(\triangle {\rm CEB}\) の向きをそろえてかくと、
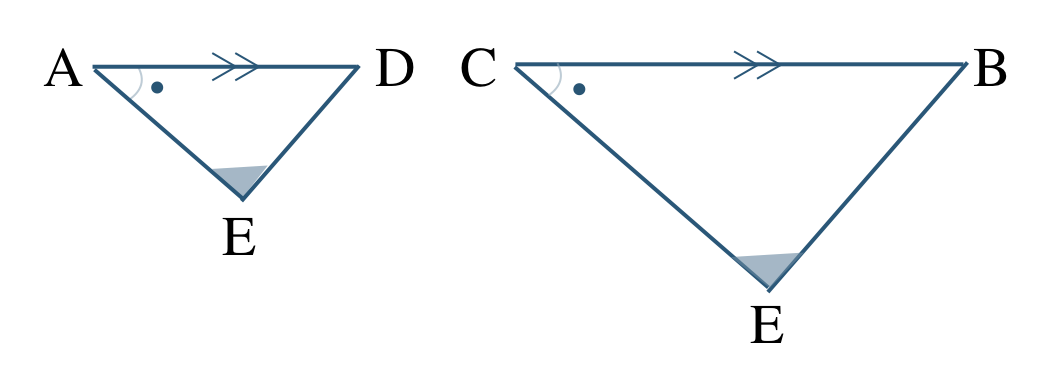
したがって、
\(\triangle {\rm AED}\,\,\unicode{x223D}\,\,\triangle {\rm CEB}\)
相似条件は、
2組の角がそれぞれ等しい
となる
問題解説(3)
次の図において、相似な三角形を見つけて、記号を使って表せ。また、そのときの相似条件を答えよ。
\({\small (3)}~\)

辺の比は、
\({\rm AE:DE}=6:9=2:3\)
\({\rm BE:CE}=4:6=2:3\)
対頂角が等しいので、
\(\angle{\rm AEB}=\angle{\rm DEC}\)
これより、\(\triangle {\rm ABE}\) と \(\triangle {\rm DCE}\) の向きをそろえてかくと、
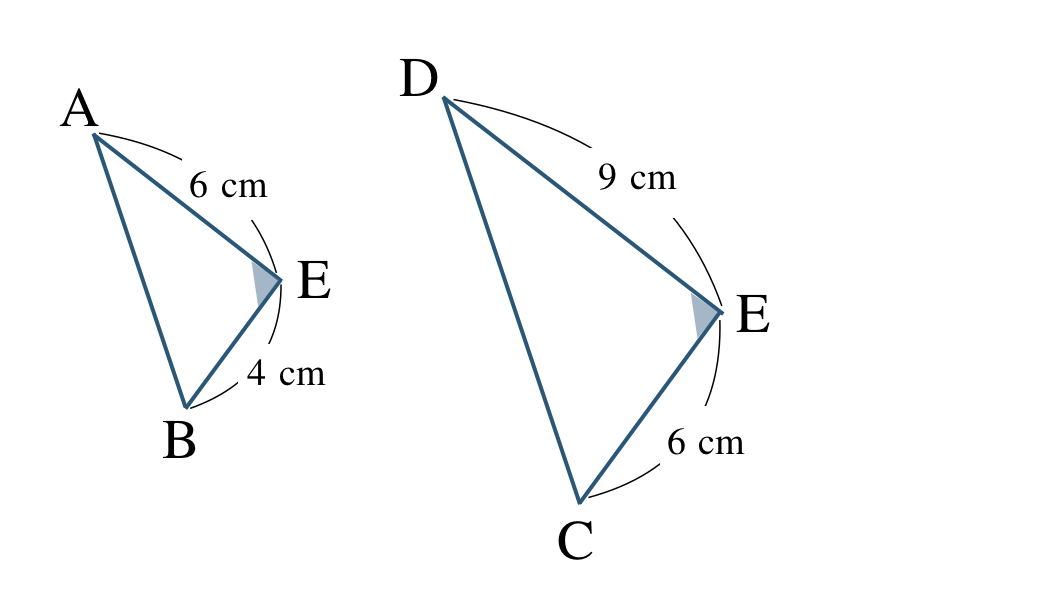
したがって、
\(\triangle {\rm ABE}\,\,\unicode{x223D}\,\,\triangle {\rm DCE}\)
相似条件は、
2組の辺の比とその間の角がそれぞれ等しい
となる
問題解説(4)
次の図において、相似な三角形を見つけて、記号を使って表せ。また、そのときの相似条件を答えよ。
\({\small (4)}~\)
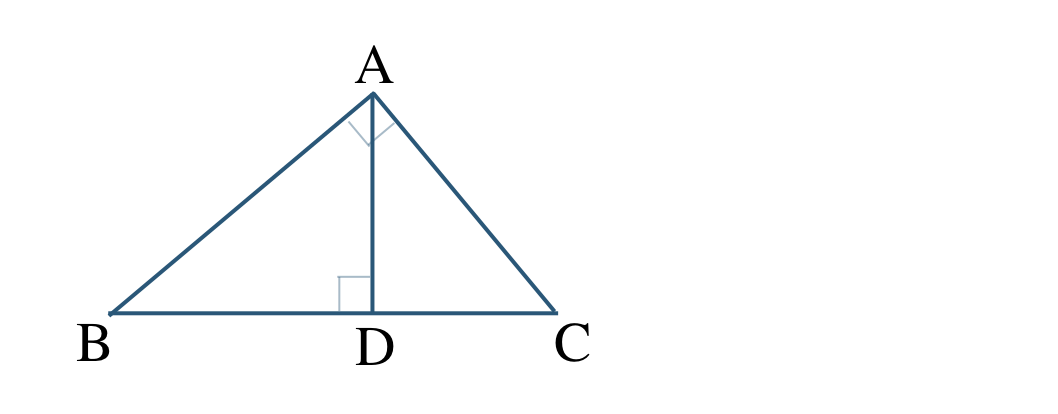

\(\angle {\rm B}\) が共通している角より、
\(\angle{\rm ABC}=\angle{\rm DBA}\)
これより、\(\triangle {\rm ABC}\) と \(\triangle {\rm DBA}\) の向きをそろえてかくと、
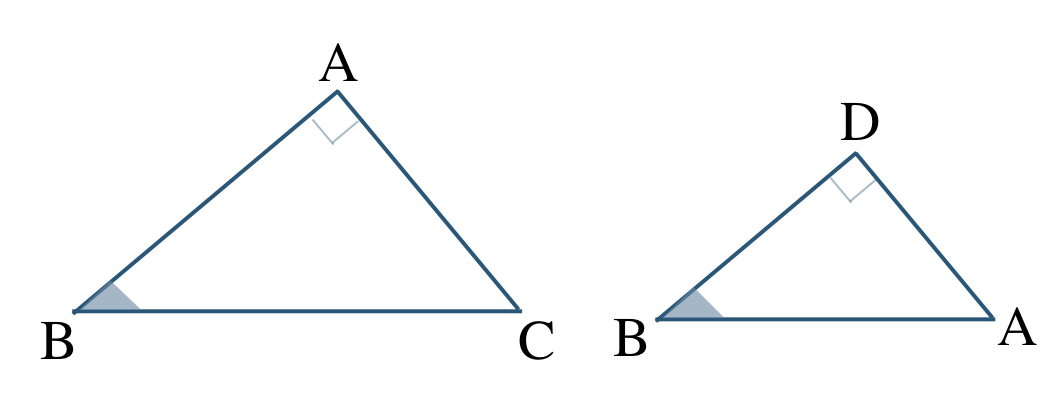
したがって、
\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm DBA}\)
相似条件は、
2組の角がそれぞれ等しい
となる

三角形の内角の和が \(180^\circ\) より、$$\begin{eqnarray}~~~\angle{\rm ABD}&=&180^\circ-(90^\circ+\angle{\rm BAD})\\[2pt]~~~&=&90^\circ-\angle{\rm BAD}\end{eqnarray}$$\(\angle {\rm A}=90^\circ\) より、
\(\angle{\rm CAD}=90^\circ-\angle{\rm BAD}\)
よって、
\(\angle{\rm ABD}=\angle{\rm CAD}\)
これより、\(\triangle {\rm ABD}\) と \(\triangle {\rm CAD}\) の向きをそろえてかくと、
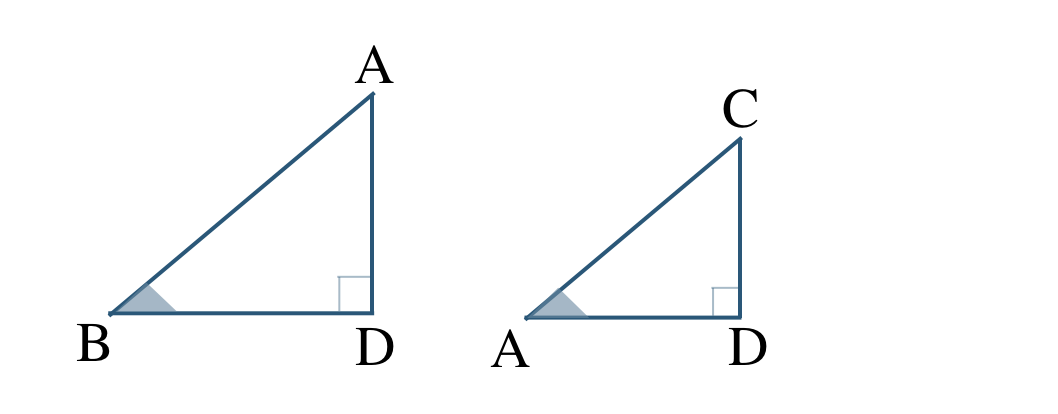
したがって、
\(\triangle {\rm ABD}\,\,\unicode{x223D}\,\,\triangle {\rm CAD}\)
相似条件は、
2組の角がそれぞれ等しい
となる

三角形の内角の和が \(180^\circ\) より、$$\begin{eqnarray}~~~\angle{\rm ABC}&=&180^\circ-(90^\circ+\angle{\rm BAD})\\[2pt]~~~&=&90^\circ-\angle{\rm BAD}\end{eqnarray}$$\(\angle {\rm A}=90^\circ\) より、
\(\angle{\rm DAC}=90^\circ-\angle{\rm BAD}\)
よって、
\(\angle{\rm ABD}=\angle{\rm DAC}\)
これより、\(\triangle {\rm ABC}\) と \(\triangle {\rm DAC}\) の向きをそろえてかくと、
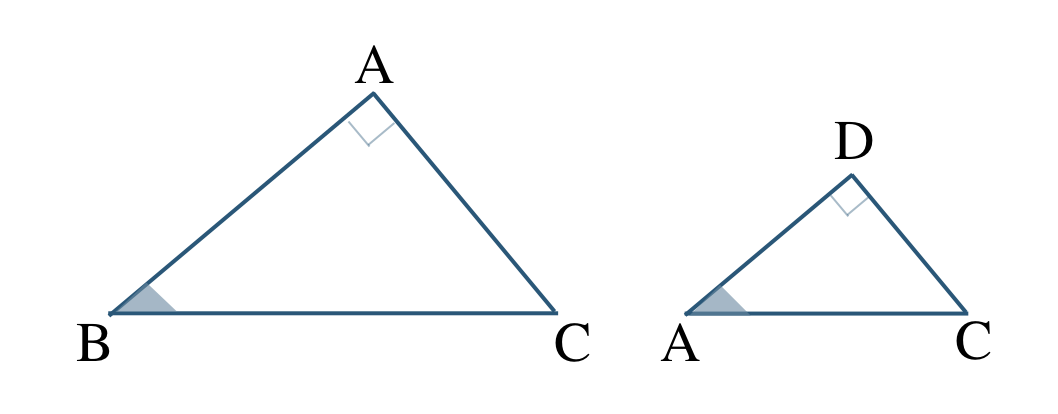
したがって、
\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm DAC}\)
相似条件は、
2組の角がそれぞれ等しい
となる



