問題:角の二等分線と比
次の問いに答えよ。
\({\small (1)}~\)\(\triangle {\rm ABC}\) の \(\angle {\rm A}\) の二等分線と辺 \({\rm BC}\) との交点を \({\rm D}\) とするとき、
\({\rm AB:AC=BD:DC}\)
を証明せよ。
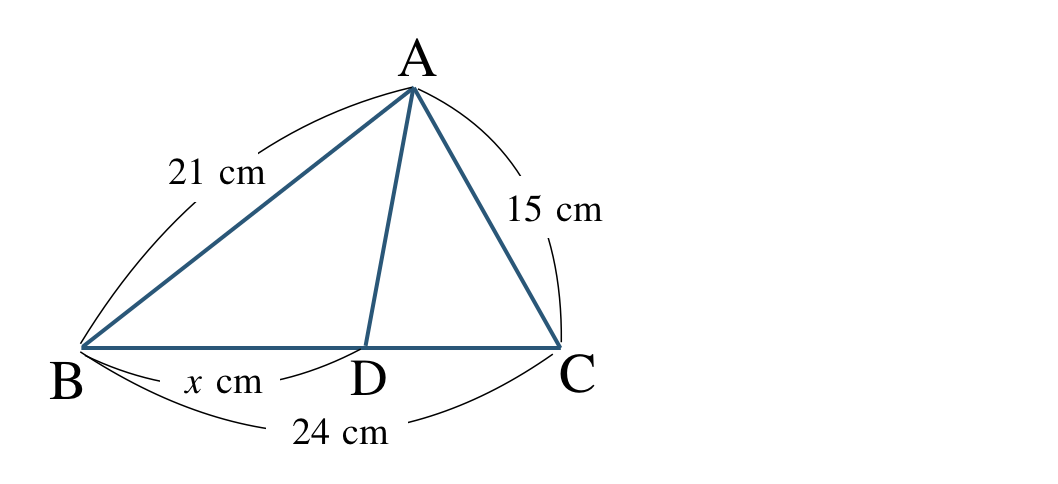
\({\small (2)}~\)\(\triangle {\rm ABC}\) の 線分 \({\rm AD}\) は \(\angle {\rm BAC}\) の二等分線であるとき、\(x\) の値を求めよ。
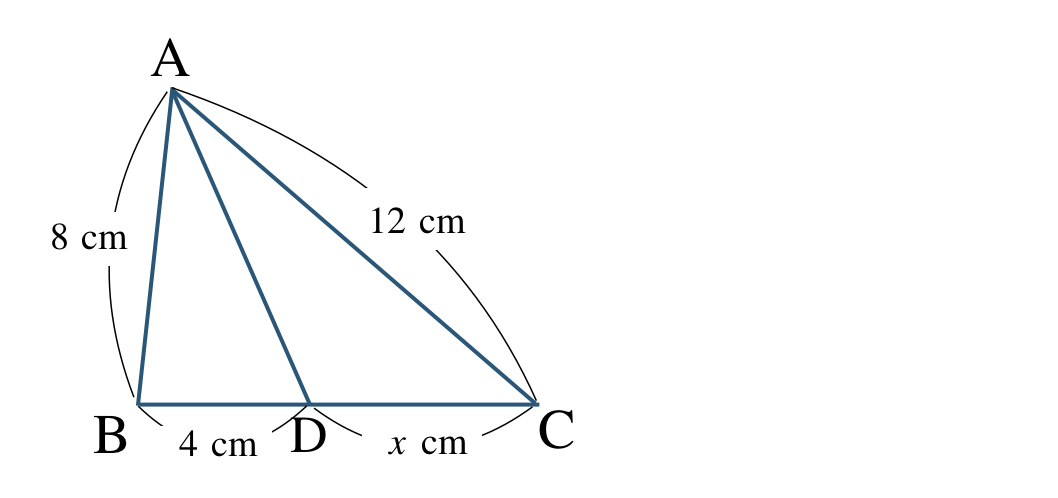
\({\small (3)}~\)\(\triangle {\rm ABC}\) の 線分 \({\rm AD}\) は \(\angle {\rm BAC}\) の二等分線であるとき、\(x\) の値を求めよ。
追加の練習問題のページはこちら→
角の二等分線と比|練習問題50問
解法のPoint
■ 角の二等分線と比
\(\triangle {\rm ABC}\) の \(\angle {\rm A}\) の二等分線と辺 \({\rm BC}\) との交点を \({\rm D}\) とすると、
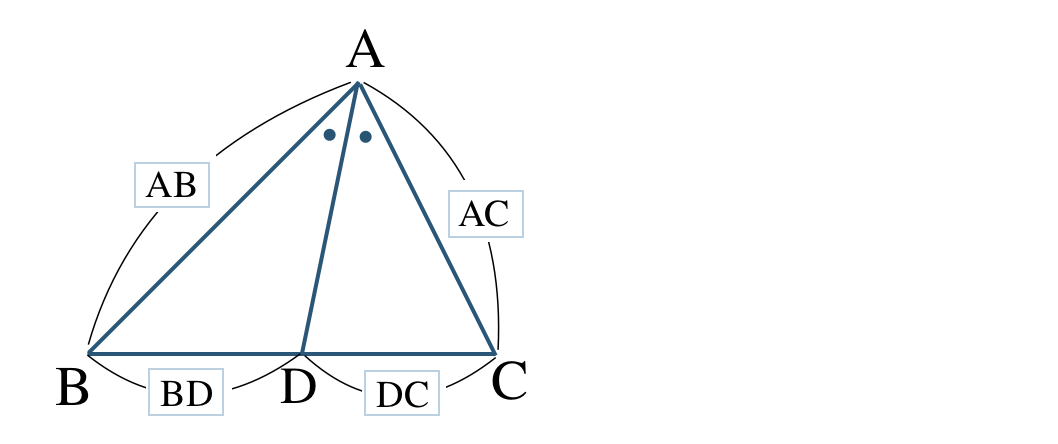
底辺 \({\rm BC}\) が2辺の比 \({\rm AB:AC}\) に分けられる。
\({\rm AB:AC=BD:DC}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:角の二等分線と比
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)\(\triangle {\rm ABC}\) の \(\angle {\rm A}\) の二等分線と辺 \({\rm BC}\) との交点を \({\rm D}\) とするとき、
\({\rm AB:AC=BD:DC}\)
を証明せよ。
[証明]
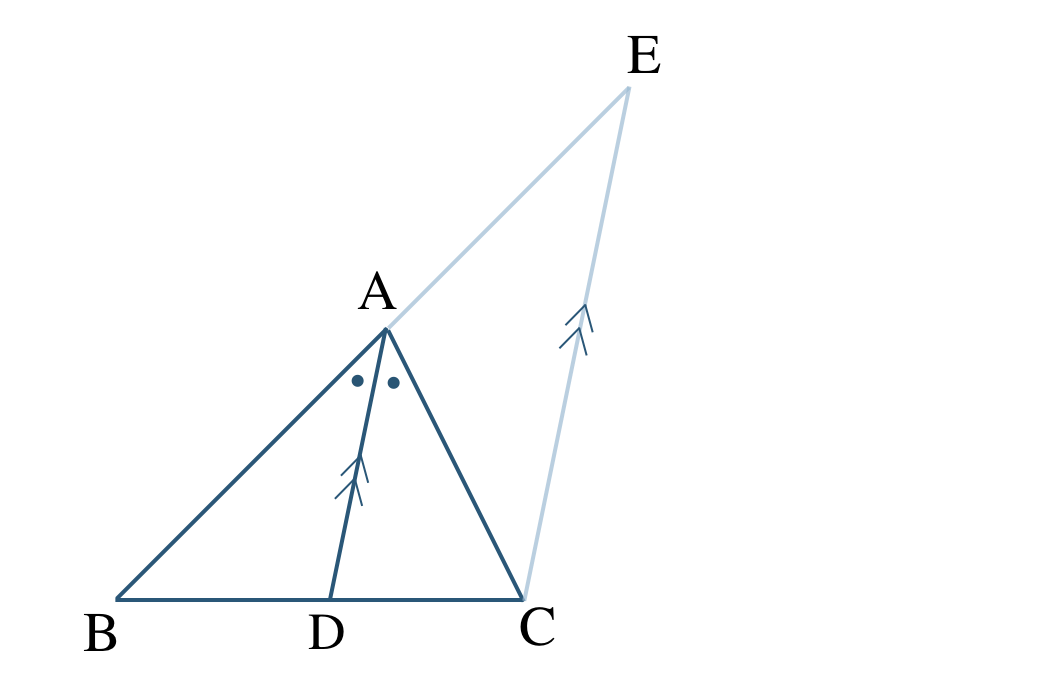
点 \({\rm C}\) を通り線分 \({\rm DA}\) に平行な直線と、辺 \({\rm AB}\) の延長線との交点を \({\rm E}\) とする
\({\rm AD\,//\,EC}\) より、同位角が等しいので、
\(\angle{\rm BAD}=\angle{\rm AEC}\)
\({\rm AD\,//\,EC}\) より、錯角が等しいので、
\(\angle{\rm DAC}=\angle{\rm ACE}\)
また、仮定より、
\(\angle{\rm BAD}=\angle{\rm DAC}\)
よって、
\(\angle{\rm AEC}=\angle{\rm ACE}\)
\(\triangle {\rm ACE}\) は二等辺三角形となり、
\({\rm AC=AE}~~\cdots{\large ①}\)
また、\(\triangle {\rm BEC}\) において、\({\rm AD\,//\,EC}\) であるので、三角形の線分の比の定理より、
\({\rm BA:AE=BD:DC}~~\cdots{\large ②}\)
①、②より、
\({\rm AB:AC=BD:DC}\)
[終]
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)\(\triangle {\rm ABC}\) の 線分 \({\rm AD}\) は \(\angle {\rm BAC}\) の二等分線であるとき、\(x\) の値を求めよ。

角の二等分線と比の関係より、
\(~~~{\rm AB:AC=BD:DC}\)
よって、
\(\begin{eqnarray}~~~8:12&=&4:x\\[2pt]~~~8{\, \small \times \,} x&=&12{\, \small \times \,}4\\[2pt]~~~8x&=&48\\[3pt]~~~\frac{\,8x\,}{\,8\,}&=&\frac{\,48\,}{\,8\,}\\[3pt]~~~x&=&6~~{\rm cm}\end{eqnarray}\)
したがって、\(x=6~{\rm cm}\) となる
問題解説(3)
次の問いに答えよ。
\({\small (3)}~\)\(\triangle {\rm ABC}\) の 線分 \({\rm AD}\) は \(\angle {\rm BAC}\) の二等分線であるとき、\(x\) の値を求めよ。

\({\rm DC}\) の長さは、\({\rm BC=BD+DC}\) より、
\(~~~{\rm DC}=24-x~~{\rm cm}\)
角の二等分線と比の関係より、
\(~~~{\rm AB:AC=BD:DC}\)
よって、
\(\begin{eqnarray}~~~21:15&=&x:24-x\\[2pt]~~~15{\, \small \times \,} x&=&21{\, \small \times \,}(24-x)\\[2pt]~~~15x&=&21{\, \small \times \,}24+21{\, \small \times \,}(-x)\\[2pt]~~~15x&=&504-21x\\[2pt]~~~15x+21x&=&504\\[2pt]~~~36x&=&504\\[3pt]~~~\frac{\,36x\,}{\,36\,}&=&\frac{\,504\,}{\,36\,}\\[3pt]~~~x&=&14~~{\rm cm}\end{eqnarray}\)
したがって、\(x=14~{\rm cm}\) となる
追加の練習問題のページはこちら→
角の二等分線と比|練習問題50問



