円の接線の長さと作図

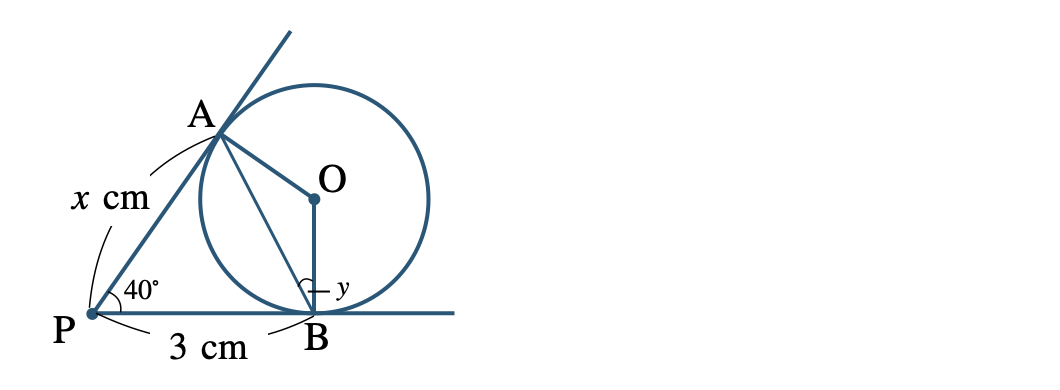
Point：円の接線の長さ

■ 円の接線

　→ \(\angle{\rm OAP}=90^\circ\)

---

　→ \({\rm PA=PB}\)

---

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

Point：円の接線の作図

円 \({\rm O}\) に外部の点 \({\rm P}\) から引いた２本の接線の作図の方法は、

① 線分 \({\rm PO}\) の垂直二等分線をひき、線分 \({\rm PO}\) との交点を \({\rm M}\) とする。
② 点 \({\rm M}\) を中心に半径 \({\rm MP(MO)}\) の円をかき、円 \({\rm O}\) との交点を \({\rm A~,~B}\) とする。
③ 直線 \({\rm PA~,~PB}\) が、点 \({\rm P}\) から円 \({\rm O}\) にひいた接線となる。

---

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

問題

次の問いに答えよ。

---

\({\small (1)}~\)円 \({\rm O}\) に外部の点 \({\rm P}\) からひいた２本の接線との接点を \({\rm A~,~B}\) とするとき、\({\rm PA=PB}\) となることを証明せよ。

[証明] \(\triangle {\rm POA}\) と \(\triangle {\rm POB}\) について、
円の接線は接点を通る半径に垂直より、
　\(\angle{\rm OAP}=\angle{\rm OBP}=90^\circ~~~\cdots{\large ①}\)
円の半径より、
　\({\rm OA=OB}~~~\cdots{\large ②}\)
共通の辺より、
　\({\rm PO=PO}~~~\cdots{\large ③}\)
①、②、③より、直角三角形の斜辺と他の１辺がそれぞれ等しいので、
　\(\triangle {\rm POA}\equiv\triangle {\rm POB}\)
合同な図形では、対応する辺は等しいので、
　\({\rm PA=PB}\)
[終]

問題

次の問いに答えよ。

---

\({\small (2)}~\)次の図の点 \({\rm P}\) を通る円 \({\rm O}\) の接線を作図せよ。

① 線分 \({\rm PO}\) の垂直二等分線をひき、線分 \({\rm PO}\) との交点を \({\rm M}\) とする。

② 点 \({\rm M}\) を中心に半径 \({\rm MP(MO)}\) の円をかき、円 \({\rm O}\) との交点を \({\rm A~,~B}\) とする。

③ 直線 \({\rm PA~,~PB}\) が、点 \({\rm P}\) から円 \({\rm O}\) にひいた接線となる。

問題

次の問いに答えよ。

---

\({\small (3)}~\)次の図で、\(x\) の長さのと \(y\) の大きさを求めよ。

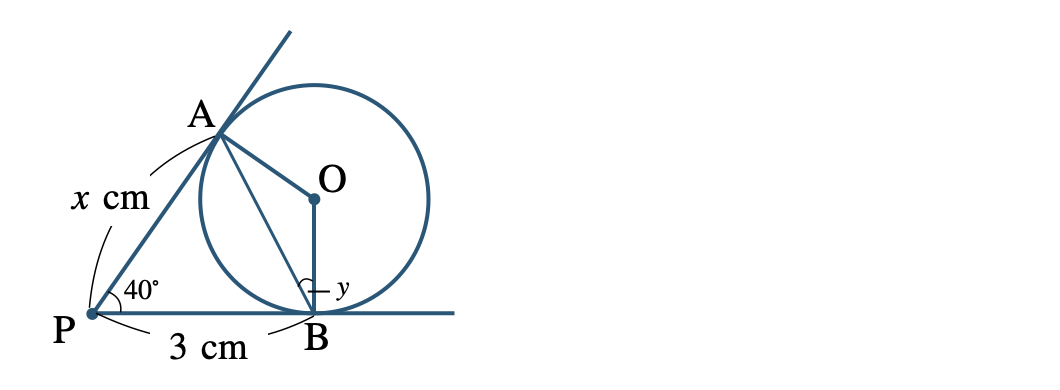
円の外部の点からひいた２本の接線の長さは等しいので、

---

\(~~~x=3~{\rm cm}\)

---

また、\(\triangle {\rm PAB}\) は \({\rm PA=PB}\) の二等辺三角形となり、底角が等しいので、
　\(\angle{\rm PAB}=\angle{\rm PBA}\)
また、三角形の内角の和が \(180^\circ\) より、

---

\(~~~\angle {\rm PBA}=\frac{\,180^\circ-40^\circ\,}{\,2\,}=\frac{\,140^\circ\,}{\,2\,}=70^\circ\)

---

また、円の接線は、接点を通る半径に垂直であるので、
　\(\angle{\rm OPB}=90^\circ\)
よって、

---

\(\begin{eqnarray}~~~y&=&\angle{\rm OPB}-\angle{\rm PBA}\\[2pt]~~~&=&90^\circ-70^\circ=20^\circ\end{eqnarray}\)

---

したがって、答えは \(x=3~{\rm cm}~,~y=20^\circ\) となる