このページは「中学数学3 三平方の定理」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう!
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。
【問題一覧】中学数学3 三平方の定理
直角三角形と三平方の定理
次の三角形で、\(x\) の値を求めよ。
\({\small (1)}~\)
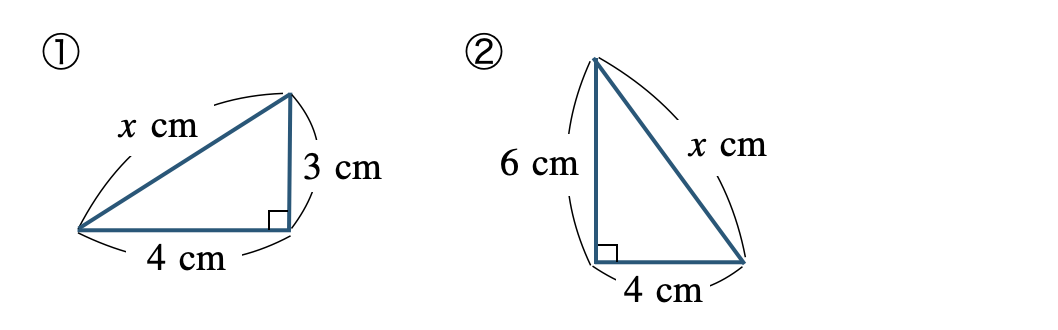
\({\small (2)}~\)

[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(x=5~{\rm cm}\) ② \(x=2\sqrt{13}~{\rm cm}\)
\({\small (2)}~\)
① \(x=5~{\rm cm}\) ② \(x=\sqrt{3}~{\rm cm}\)

三平方の定理の逆
三角形の3辺の長さが次のとき、この三角形が直角三角形であるか調べよ。
\({\small (1)}~3~{\rm cm}~,~6~{\rm cm}~,~8~{\rm cm}\)
\({\small (2)}~6~{\rm cm}~,~8~{\rm cm}~,~10~{\rm cm}\)
\({\small (3)}~5~{\rm cm}~,~5~{\rm cm}~,~5\sqrt{2}~{\rm cm}\)
\({\small (4)}~\sqrt{13}~{\rm cm}~,~\sqrt{17}~{\rm cm}~,~\sqrt{39}~{\rm cm}\)
\({\small (5)}~\sqrt{2}~{\rm cm}~,~\sqrt{6}~{\rm cm}~,~2\sqrt{2}~{\rm cm}\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)直角三角形でない
\({\small (2)}~\)直角三角形である
\({\small (3)}~\)直角三角形である
\({\small (4)}~\)直角三角形でない
\({\small (5)}~\)直角三角形である

特別な直角三角形
次の問いに答えよ。
\({\small (1)}~\)次の図で、\(x~,~y\) の値を求めよ。
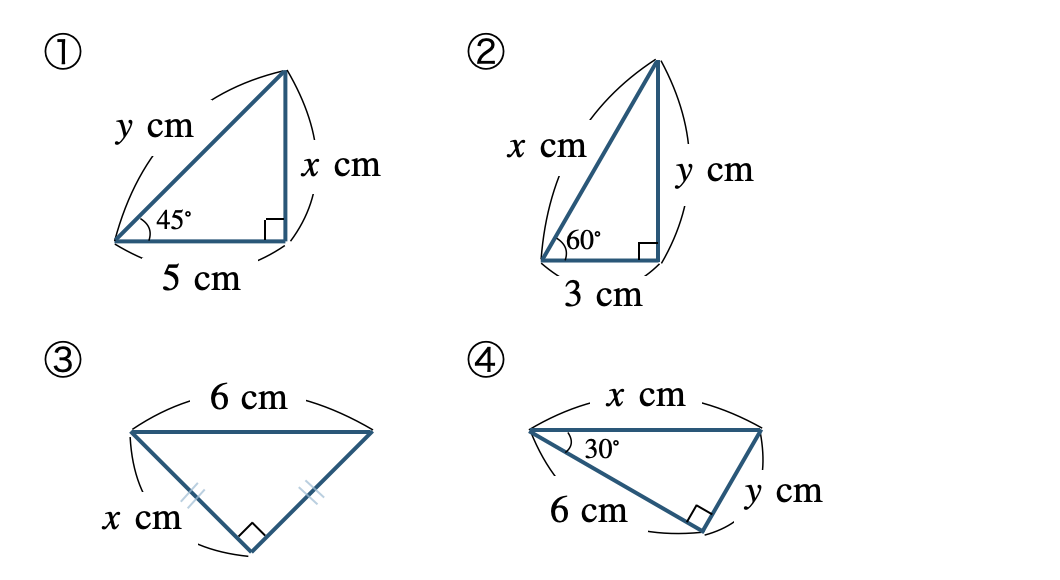
\({\small (2)}~\)1組の三角定規を次のように合わせる。\({\rm AC}=6~{\rm cm}\) のとき、残りの辺の長さを求めよ。

[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(x=5~{\rm cm}~,~y=5\sqrt{2}~{\rm cm}\)
② \(x=6~{\rm cm}~,~y=3\sqrt{3}~{\rm cm}\)
③ \(x=3\sqrt{2}~{\rm cm}\)
④ \(x=4\sqrt{3}~{\rm cm}~,~y=2\sqrt{3}~{\rm cm}\)
\({\small (2)}~\)
\({\rm AB}=3\sqrt{2}~{\rm cm}~,~{\rm BC}=3\sqrt{2}~{\rm cm}\)
\({\rm CD}=2\sqrt{3}~{\rm cm}~,~{\rm AD}=4\sqrt{3}~{\rm cm}\)

図形と三平方の定理
次の問いに答えよ。
\({\small (1)}~\)次の長方形の対角線の長さを求めよ。

\({\small (2)}~\)1辺の長さが \(6~{\rm cm}\) の正三角形 \(\triangle {\rm ABC}\) の面積を求めよ。
\({\small (3)}~\)次の二等辺三角形 \(\triangle {\rm ABC}\) の面積を求めよ。

[ 解答を見る ]
【解答】
\({\small (1)}~6~{\rm cm}\)
\({\small (2)}~9\sqrt{3}~{\rm cm}^2\)
\({\small (3)}~12~{\rm cm}^2\)

円と三平方の定理
次の問いに答えよ。
\({\small (1)}~\)半径 \(6~{\rm cm}\) の円 \({\rm O}\) において、中心 \({\rm O}\) からの距離が \(3~{\rm cm}\) である弦 \({\rm AB}\) の長さを求めよ。

\({\small (2)}~\)次の図で、直線 \({\rm AP}\) は円 \({\rm O}\) の接線で、点 \({\rm P}\) は接点である。円 \({\rm O}\) の半径が \(6~{\rm cm}\)、\({\rm AO}=12~{\rm cm}\) のとき、接線 \({\rm AP}\) の長さを求めよ。

[ 解答を見る ]
【解答】
\({\small (1)}~6\sqrt{3}~{\rm cm}\)
\({\small (2)}~6\sqrt{3}~{\rm cm}\)

√nの作図
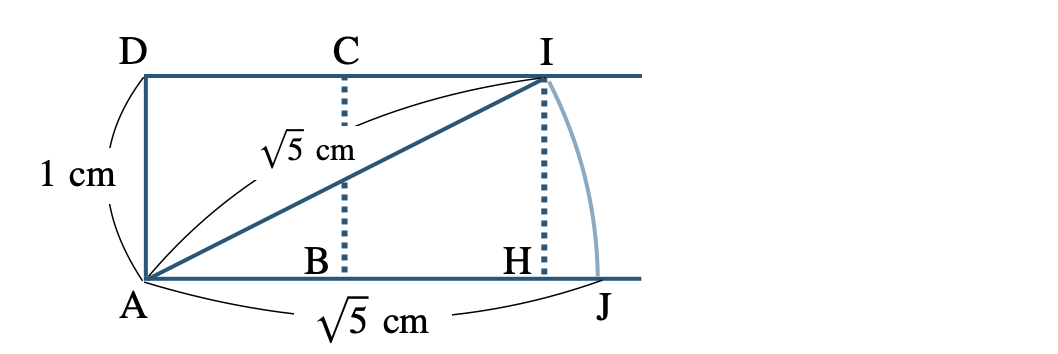
次の図において、下の問いに答えよ。

\({\small (1)}~\)直線 \({\rm AB}\) 上に \(\sqrt{2}\) を作図せよ。
\({\small (2)}~\)\(\sqrt{2}\) の長さを使って、直線 \({\rm AB}\) 上に \(\sqrt{3}\) を作図せよ。
\({\small (3)}~\)直線 \({\rm AB}\) 上に \(\sqrt{5}\) を作図せよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)

\({\small (2)}~\)

\({\small (3)}~\)

座標上の2点間の距離
次の2点間の距離 \({\rm AB}\) を求めよ。
\({\small (1)}~{\rm A}(2~,~1)~,~{\rm B}(5~,~4)\)
\({\small (2)}~{\rm A}(-1~,~3)~,~{\rm B}(2~,~-1)\)
\({\small (3)}~{\rm A}(3~,~-5)~,~{\rm B}(-2~,~7)\)
\({\small (4)}~{\rm A}(4~,~5)~,~{\rm B}(-4~,~1)\)
[ 解答を見る ]
【解答】
\({\small (1)}~{\rm AB}=3\sqrt{2}\)
\({\small (2)}~{\rm AB}=5\)
\({\small (3)}~{\rm AB}=13\)
\({\small (4)}~{\rm AB}=4\sqrt{5}\)

立体と三平方の定理
次の問いに答えよ。
\({\small (1)}~\)次の立方体の対角線の長さを求めよ。
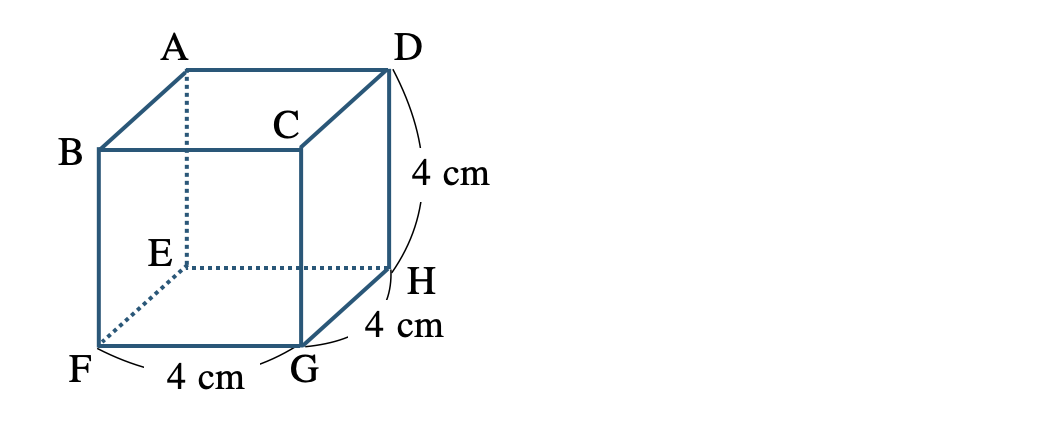
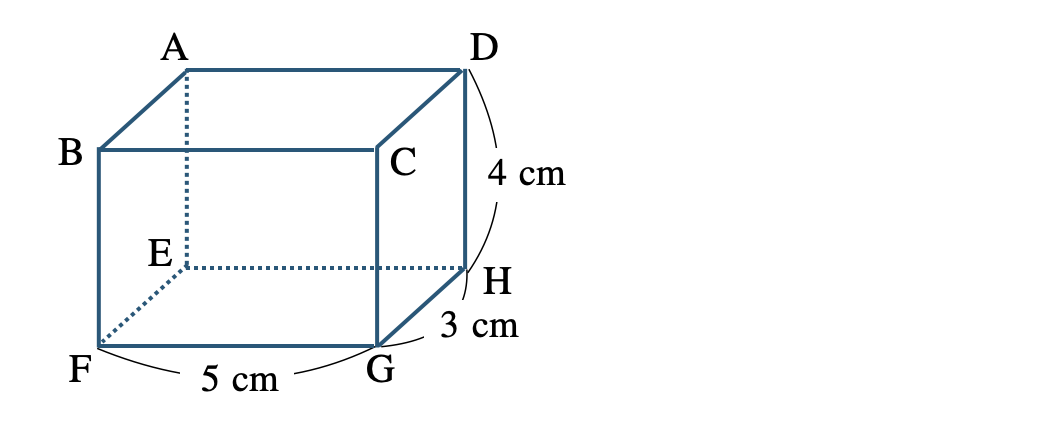
\({\small (2)}~\)次の直方体の対角線の長さを求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~4\sqrt{3}~{\rm cm}\)
\({\small (2)}~5\sqrt{2}~{\rm cm}\)

角錐や円錐と三平方の定理
次の問いに答えよ。
\({\small (1)}~\)次の正四角錐の高さと体積を求めよ。

\({\small (2)}~\)次の円錐の高さと体積を求めよ。

[ 解答を見る ]
【解答】
\({\small (1)}~\)
高さ \(3\sqrt{7}~{\rm cm}\)、体積 \(36\sqrt{7}~{\rm cm}^3\)
\({\small (2)}~\)
高さ \(5\sqrt{3}~{\rm cm}\)、体積 \(\begin{split}{\frac{\,125\sqrt{3}\pi\,}{\,3\,}}~{\rm cm}^3\end{split}\)

立体上の最短距離
次の問いに答えよ。
\({\small (1)}~\)次の図のような1辺が \(6~{\rm cm}\) の立方体において、点 \({\rm A}\) から点 \({\rm G}\) までひもをかけるとき、ひもの長さが最短になる長さを求めよ。

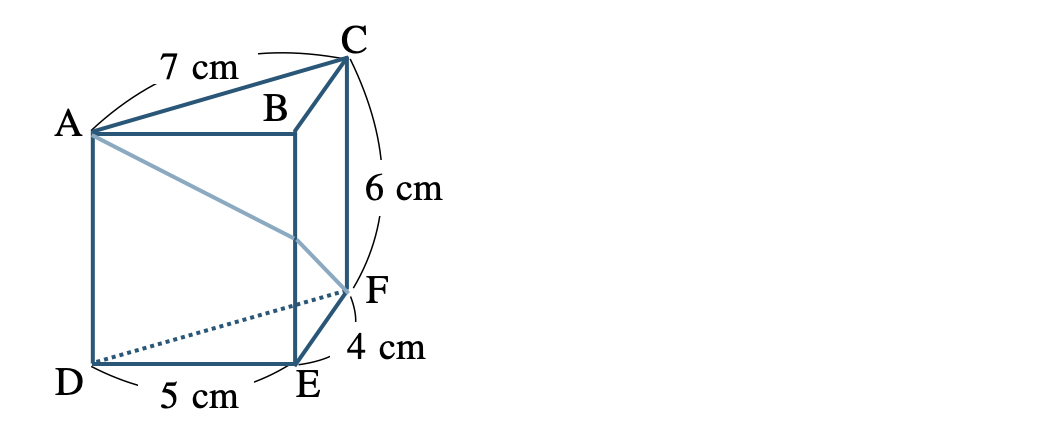
\({\small (2)}~\)次の図のような三角柱において、点 \({\rm A}\) から点 \({\rm F}\) までひもをかけるとき、ひもの長さが最短になる長さを求めよ。
[ 解答を見る ]
【解答】
\({\small (1)}~6\sqrt{5}~{\rm cm}\)
\({\small (2)}~3\sqrt{13}~{\rm cm}\)



