問題:立体と三平方の定理
問題
\({\small (1)}~\)次の立方体の対角線の長さを求めよ。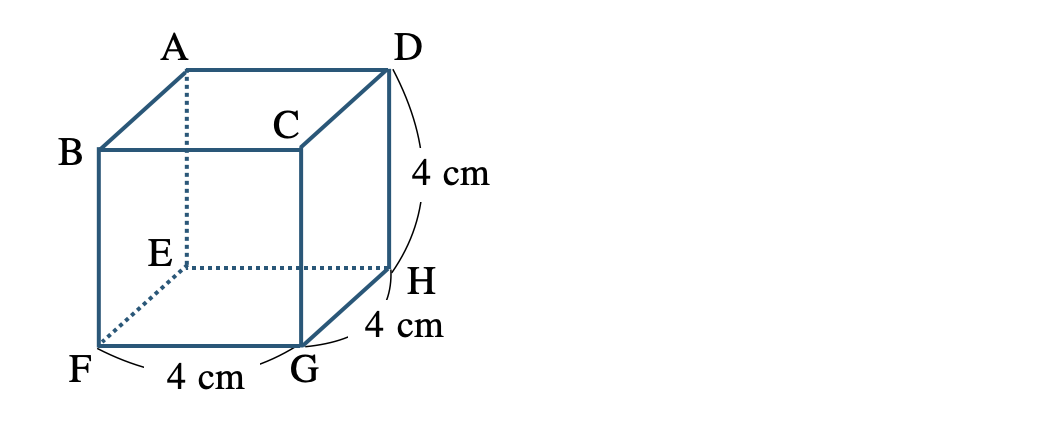
次の問いに答えよ。
\({\small (1)}~\)次の立方体の対角線の長さを求めよ。

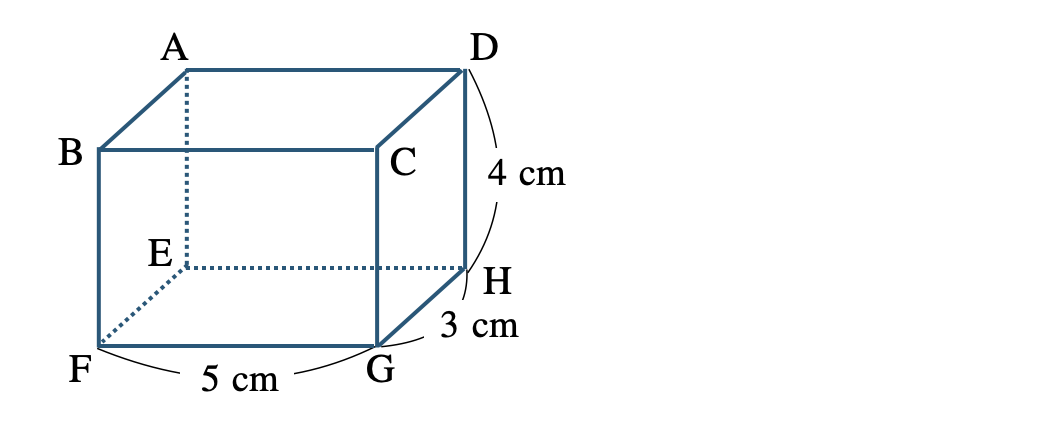
\({\small (2)}~\)次の直方体の対角線の長さを求めよ。

解法のPoint
Point:直方体の対角線
① 長方形 \({\rm EFGH}\) を考えて、この対角線 \({\rm EG}\) の2乗を三平方の定理より求める。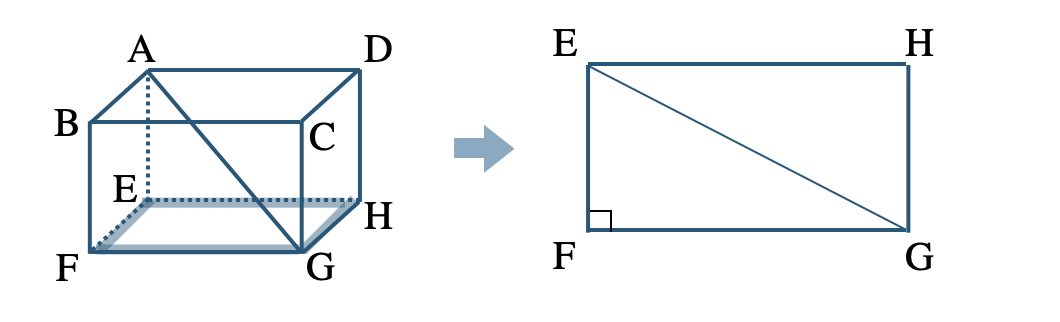
② 断面の長方形 \({\rm AEGC}\) の対角線 \({\rm AG}\) を三平方の定理より求める。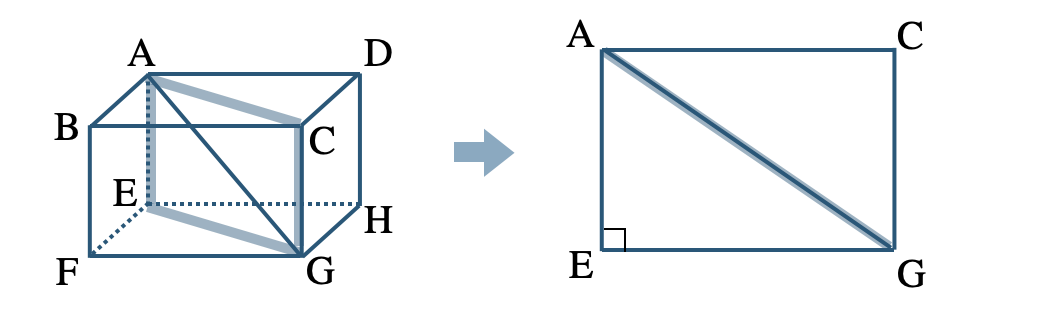
①より、
\(~~~{\rm AG^2=AE^2+EF^2+FG^2}\)
\({\rm AG}>0\) より、\({\rm AG}\) の長さを求める。
直方体 \({\rm ABCD-EFGH}\) の対角線の長さは、
① 長方形 \({\rm EFGH}\) を考えて、この対角線 \({\rm EG}\) の2乗を三平方の定理より求める。

\(~~~{\rm EG^2=EF^2+FG^2}\)
② 断面の長方形 \({\rm AEGC}\) の対角線 \({\rm AG}\) を三平方の定理より求める。

\(~~~{\rm AG^2=AE^2+EG^2}\)
①より、
\(~~~{\rm AG^2=AE^2+EF^2+FG^2}\)
\({\rm AG}>0\) より、\({\rm AG}\) の長さを求める。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
Point:直方体の対角線の公式
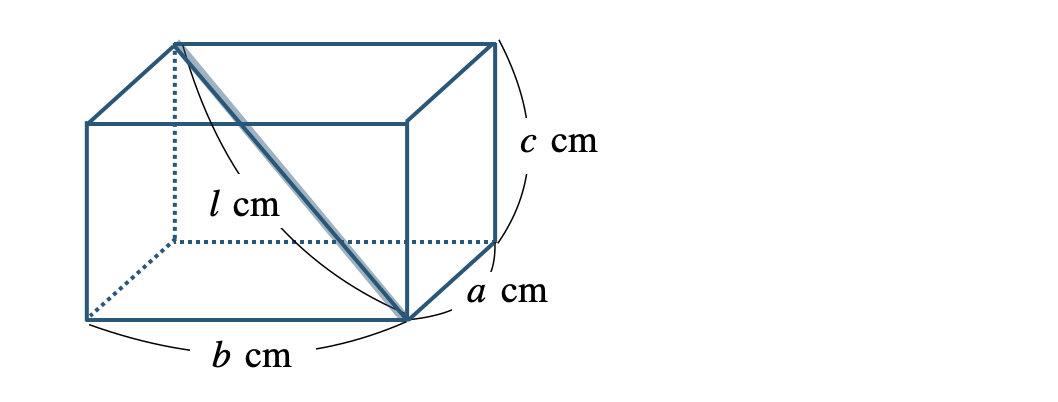
\(l=\sqrt{a^2+b^2+c^2}\)

縦 \(a~{\rm cm}\)、横 \(b~{\rm cm}\)、高さ \(c~{\rm cm}\) の直方体の対角線の長さ \(l~{\rm cm}\) の式は、
\(l=\sqrt{a^2+b^2+c^2}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:立体と三平方の定理
問題解説(1)
問題
\({\small (1)}~\)次の立方体の対角線の長さを求めよ。
次の問いに答えよ。
\({\small (1)}~\)次の立方体の対角線の長さを求めよ。

正方形 \({\rm EFGH}\) について、
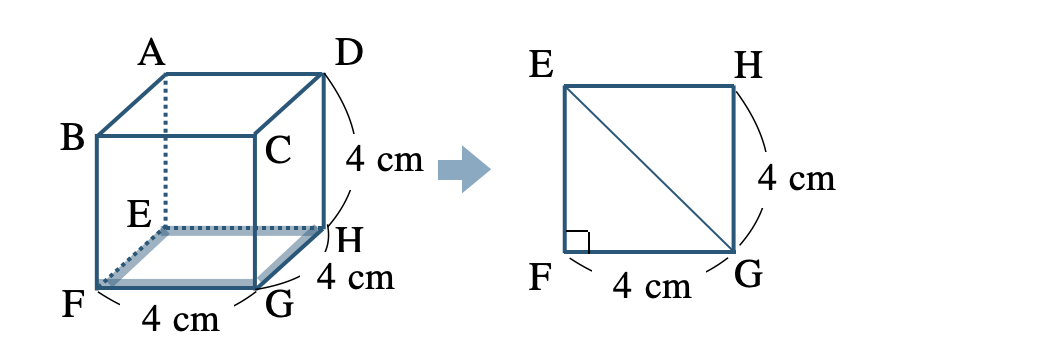
この対角線 \({\rm EG}\) の2乗は三平方の定理より、
\(\begin{eqnarray}~~~{\rm EG}^2&=&4^2+4^2\\[2pt]~~~&=&16+16\\[2pt]~~~&=&32\end{eqnarray}\)
次に、断面の長方形 \({\rm AEGC}\) について、
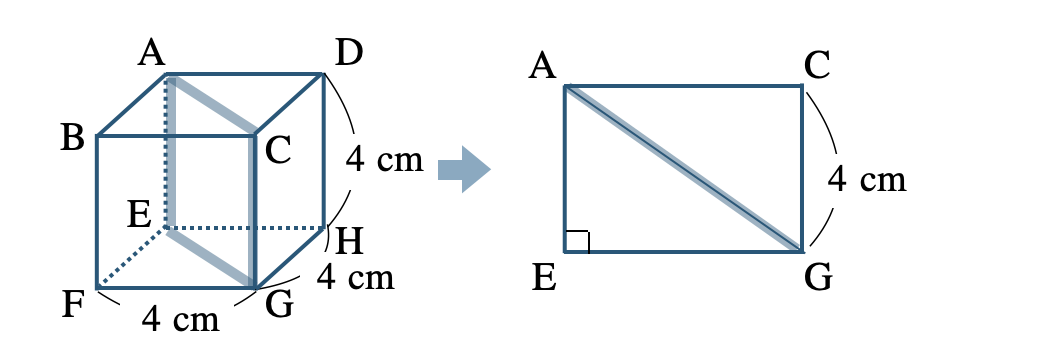
対角線 \({\rm AG}\) の長さは、三平方の定理より、
\(~~~{\rm AG}^2=4^2+{\rm EG}^2\)
\({\rm EG}^2=32\) より、
\(\begin{eqnarray}~~~{\rm AG}^2&=&16+32\\[2pt]~~~&=&48\end{eqnarray}\)
\({\rm AG}>0\) より、
\(~~~{\rm AG}=\sqrt{48}=\sqrt{4^2\times3}=4\sqrt{3}\)
したがって、答えは \(4\sqrt{3}~{\rm cm}\) となる
【別解】
対角線を \(l~{\rm cm}\) とすると、対角線の公式より、
\(\begin{eqnarray}~~~l^2&=&4^2+4^2+4^2\\[2pt]~~~&=&16+16+16\\[2pt]~~~&=&48\end{eqnarray}\)
\(l>0\) より、
\(~~~l=\sqrt{48}=\sqrt{4^2\times3}=4\sqrt{3}\)
したがって、答えは \(4\sqrt{3}~{\rm cm}\) となる
問題解説(2)
問題
\({\small (2)}~\)次の直方体の対角線の長さを求めよ。
次の問いに答えよ。
\({\small (2)}~\)次の直方体の対角線の長さを求めよ。

長方形 \({\rm EFGH}\) について、
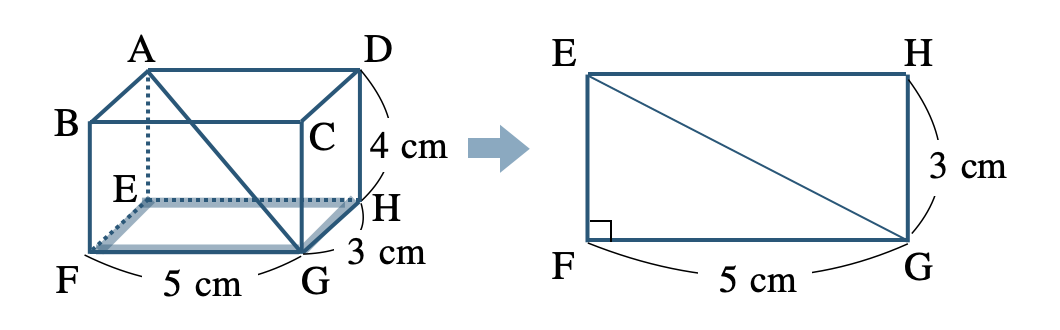
この対角線 \({\rm EG}\) の2乗は三平方の定理より、
\(\begin{eqnarray}~~~{\rm EG}^2&=&3^2+5^2\\[2pt]~~~&=&9+25\\[2pt]~~~&=&34\end{eqnarray}\)
次に、断面の長方形 \({\rm AEGC}\) について、
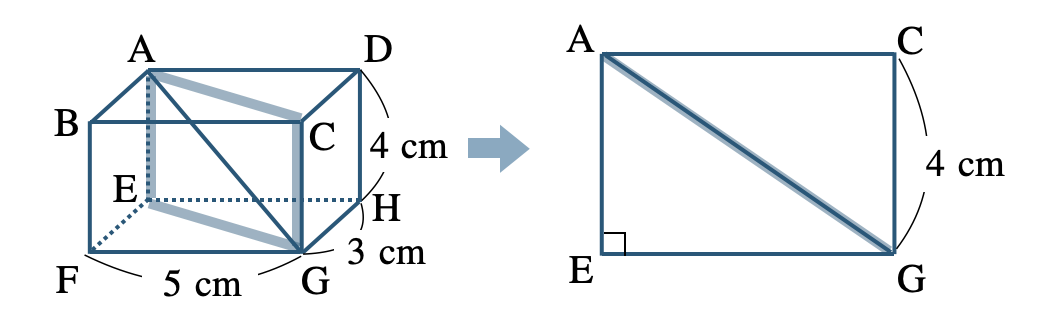
対角線 \({\rm AG}\) の長さは、三平方の定理より、
\(~~~{\rm AG}^2=4^2+{\rm EG}^2\)
\({\rm EG}^2=32\) より、
\(\begin{eqnarray}~~~{\rm AG}^2&=&16+34\\[2pt]~~~&=&50\end{eqnarray}\)
\({\rm AG}>0\) より、
\(~~~{\rm AG}=\sqrt{50}=\sqrt{5^2\times2}=5\sqrt{2}\)
したがって、答えは \(5\sqrt{2}~{\rm cm}\) となる
【別解】
対角線を \(l~{\rm cm}\) とすると、対角線の公式より、
\(\begin{eqnarray}~~~l^2&=&3^2+5^2+4^2\\[2pt]~~~&=&9+25+16\\[2pt]~~~&=&50\end{eqnarray}\)
\(l>0\) より、
\(~~~l=\sqrt{50}=\sqrt{5^2\times2}=5\sqrt{2}\)
したがって、答えは \(5\sqrt{2}~{\rm cm}\) となる

【問題一覧】中3|三平方の定理
このページは「中学数学3 三平方の定理」の問題一覧ページとなります。解説の見たい単元名がわからないと...


