標本調査と推定

Point：標本調査と推定

母集団から無作為に抽出した標本において、
　母集団の比＝標本の比
これを使い、値を推定することができる。

---

たとえば、白玉と黒玉が合わせて \(100\) 個あり、\(20\) 個を無作為に抽出したところ。\(7\) 個が白玉であった。このとき、\(100\) 個の中で白玉は何個あると推測できるかは、

---

① 求めたい値を \(x\) とする。
　\(100\) 個の中で白玉を \(x\) 個とする

---

② 母集団の数と条件に合う数、標本の大きさと条件に合う数をそれぞれ確認する。
　母集団では、\(100\) 個の中で \(x\) 個
　標本では、\(20\) 個の中で \(7\) 個

---

③ 母集団の比＝標本の比を使い求めたい数を計算する。

---

　\(\begin{eqnarray}~~~100:x&=&20:7
\\[2pt]~~~x&=&35
\end{eqnarray}\)

---

　これより、\(35\) 個

---

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

問題

次の問いに答えよ。

---

\({\small (1)}~\)ある工場で作られた品物 \(10000\) 個の中から \(250\) 個を無作為に抽出したところ \(3\) 個が不良品であった。
作られた \(10000\) 個の品物の中で不良品は何個と推定されるか答えよ。

母集団の品物 \(10000\) 個の中の不良品の数を \(x\) 個とする
標本の大きさ \(250\) 個の中に不良品が \(3\) 個あるので、

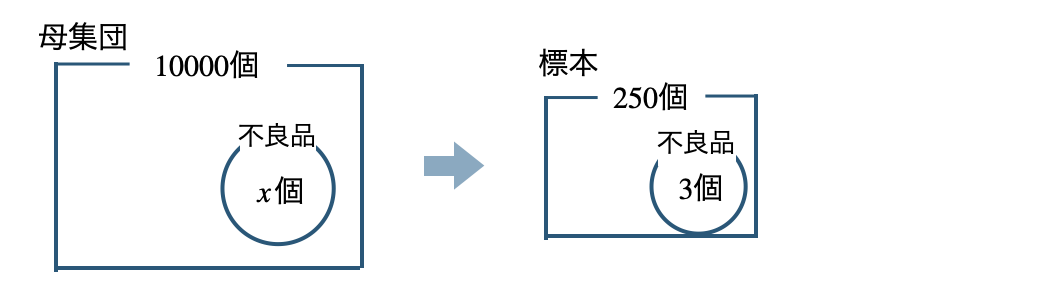
母集団の不良品の比＝標本の不良品の比より、

---

\(\begin{eqnarray}~~~10000:x&=&250:3\\[2pt]~~~x \times 250&=&10000\times3\\[2pt]~~~250x&=&30000\\[3pt]~~~\frac{\,250x\,}{\,250\,}&=&\frac{\,30000\,}{\,250\,}\\[3pt]~~~x&=&120\end{eqnarray}\)

---

したがって、不良品は \(120\) 個と推定される

問題

次の問いに答えよ。

---

\({\small (2)}~\)池の魚の数を調べるために、池のあちこちで魚 \(100\) 匹を捕獲して、印を付けて池に戻した。後日、同じように \(120\) 匹を捕獲して、印の付いた魚の数を数えたところ \(48\) 匹であった。
このとき、池の魚の数を推定して答えよ。

母集団の池の魚の数を \(x\) 匹とすると、この中で印を付けた魚は \(100\) 匹である
標本の大きさは \(120\) 匹で、この中で印が付いている魚は \(48\) 匹であるので、

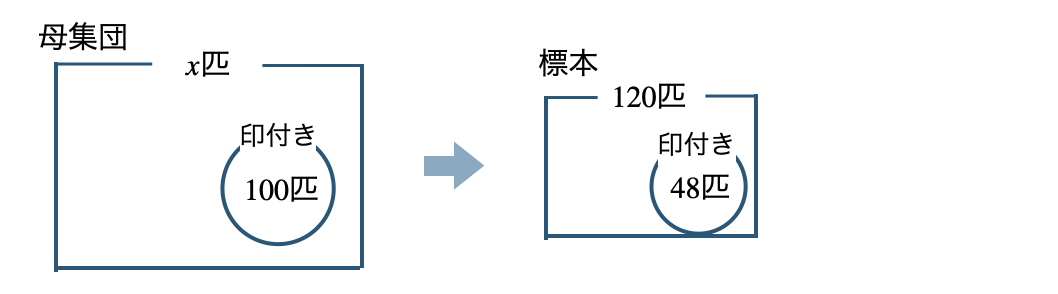
母集団の印付きの比＝標本の印付きの比より、

---

\(\begin{eqnarray}~~~x:100&=&120:48
\\[2pt]~~~x\times48&=&100\times120\\[2pt]~~~48x&=&12000\\[3pt]~~~\frac{\,48x\,}{\,48\,}&=&\frac{\,12000\,}{\,48\,}\\[3pt]~~~x&=&250\end{eqnarray}\)

---

したがって、池の魚の数は \(250\) 匹と推定できる

問題

次の問いに答えよ。

---

\({\small (3)}~\)箱に大量の白玉が入っている。同じ形、大きさの赤玉を \(100\) 個入れて、そこから \(50\) 個の玉を無作為に抽出すると、赤玉が \(20\) 個ふくまれていた。
このとき、はじめに入っていた白玉は何個と推定されるか答えよ。

母集団の白玉の数を \(x\) 個とすると、赤玉と合わせて合計 \(x+100\) 個になり、この中に赤玉は \(100\) 個ある
標本の大きさ \(50\) 個の中で赤玉は \(20\) 個であるので、

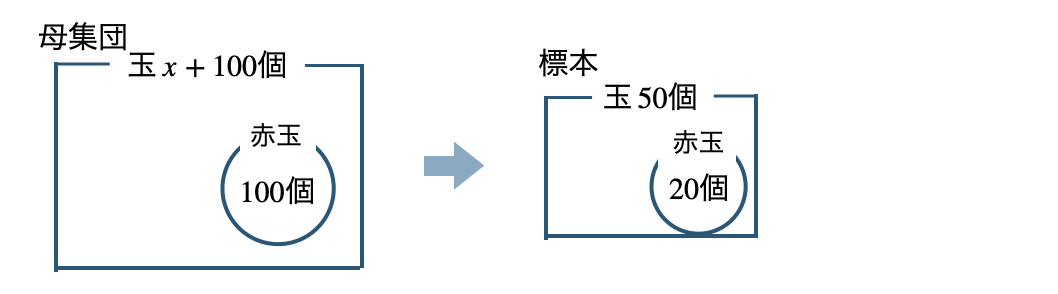
母集団の赤玉の比＝標本の赤玉の比より、

---

\(\begin{eqnarray}~~~x+100:100&=&50:20
\\[2pt]~~~(x+100)\times20&=&100\times50\\[2pt]~~~20x+2000&=&5000\\[2pt]~~~20x&=&5000-2000\\[2pt]~~~20x&=&3000\\[3pt]~~~\frac{\,20x\,}{\,20\,}&=&\frac{\,3000\,}{\,20\,}\\[3pt]~~~x&=&150\end{eqnarray}\)

---

したがって、箱の中の白玉の数は \(150\) 個と推定できる