問題:玉を取り出す確率
赤玉3個、白玉2個の入った袋から同時に2個の玉を取り出すとき、次の確率を求めよ。
\({\small (1)}~\)赤玉2個を取り出す確率
\({\small (2)}~\)赤玉1個と白玉1個を取り出す確率
\({\small (3)}~\)同じ色の玉を取り出す確率
さらに、この袋に青玉1個を入れて同時に2個の玉を取り出すとき、次の確率を求めよ。
\({\small (4)}~\)赤玉1個と青玉1個を取り出す確率
\({\small (5)}~\)違う色の玉を取り出す確率
追加の練習問題のページはこちら→
玉を2個同時に取り出す確率|練習問題15問+15問
解法のPoint
白玉2個、黒玉2個の入った袋から同時に2個の玉を取り出すとき、同じ色の玉である確率は、
① すべての玉を区別して考える。
白玉2個を ① ②、黒玉2個を \(\fbox{3}\) \(\fbox{4}\) と
4つ玉をすべてを区別する。
② 2個を取り出すときは、選ぶだけのパターンとして樹形図をかく。
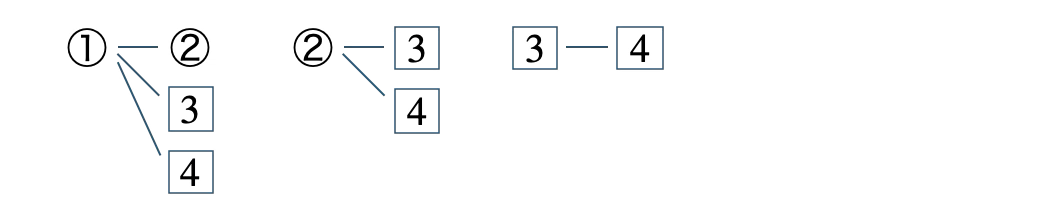
※ ① – ② と ② – ① は同じになるので注意。
これより、すべての場合の数は \(6\) 通り
③ 条件に合う場合の数を数えて、確率を求める。
同じ色の玉の場合の数は、
① – ② と \(\fbox{3}\) – \(\fbox{4}\) の \(2\) 通りあるので、
確率は、\(\displaystyle \frac{\,2\,}{\,6\,}=\displaystyle \frac{\,1\,}{\,3\,}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
トランプを使った問題も同じ考え方で解けます。
例えば ♡2、♡3、♠︎4、♠︎5 の4枚から2枚を同時に取り出すとき、同じマークになる確率を求める問題は、玉を取り出す確率の考え方と同じです。

樹形図のかき方はこちらから↓

問題解説:玉を取り出す確率
問題解説(1)
赤玉3個、白玉2個の入った袋から同時に2個の玉を取り出すとき、次の確率を求めよ。
\({\small (1)}~\)赤玉2個を取り出す確率
赤玉3個、白玉2個を、
赤玉3個を \(\fbox{1}\) \(\fbox{2}\) \(\fbox{3}\)、白玉2個を ④ ⑤
と区別して考える
この中から2個を取り出すとき、選ぶだけのパターンとなり樹形図をかくと、
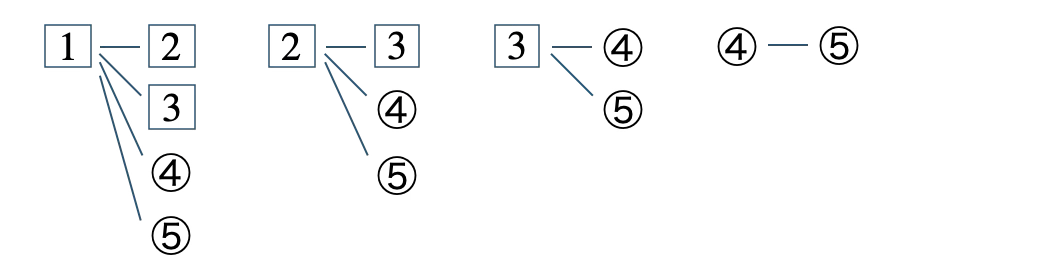
※ \(\fbox{1}\) – \(\fbox{2}\) と \(\fbox{2}\) – \(\fbox{1}\) は同じになるので注意。
これより、すべての場合の数は、
\(~~~4+3+2+1=10\)
\(10\) 通りとなり、同様に確からしい
ここで、この中で赤玉2個を取り出すのは、
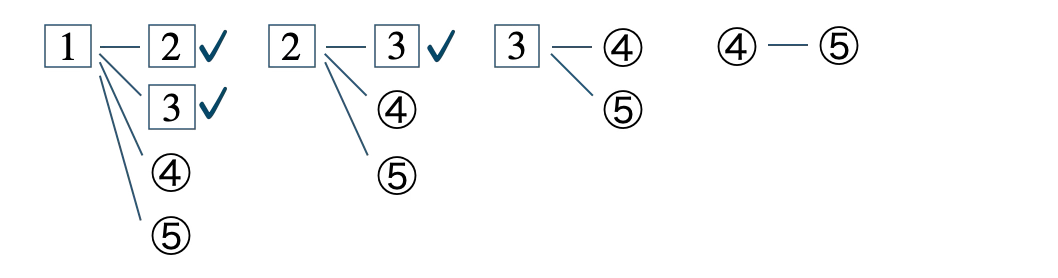
✓を付けた \(3\) 通りである
したがって、確率は \({\displaystyle \frac{\,3\,}{\,10\,}}\) となる
問題解説(2)
赤玉3個、白玉2個の入った袋から同時に2個の玉を取り出すとき、次の確率を求めよ。
\({\small (2)}~\)赤玉1個と白玉1個を取り出す確率
起こりうるすべての場合の数は \(10\) 通りである
この中で赤玉1個と白玉1個を取り出すのは、
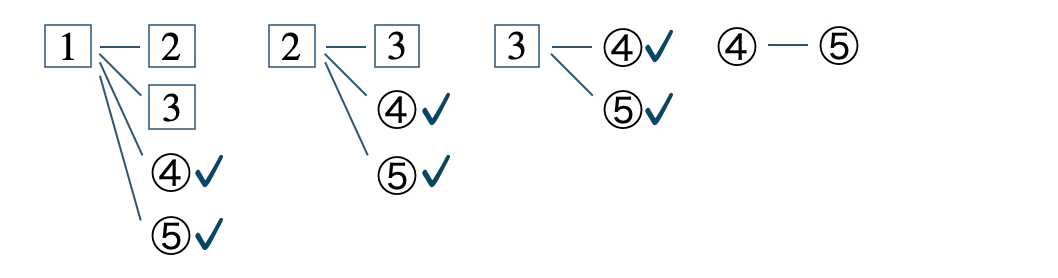
✓を付けた \(6\) 通りであるので、確率は、
\(~~~\displaystyle \frac{\,6\,}{\,10\,}=\displaystyle \frac{\,3\,}{\,5\,}\)
したがって、答えは \({\displaystyle \frac{\,3\,}{\,5\,}}\) となる
問題解説(3)
赤玉3個、白玉2個の入った袋から同時に2個の玉を取り出すとき、次の確率を求めよ。
\({\small (3)}~\)同じ色の玉を取り出す確率
起こりうるすべての場合の数は \(10\) 通りである
この中で同じ色の玉を取り出すのは、
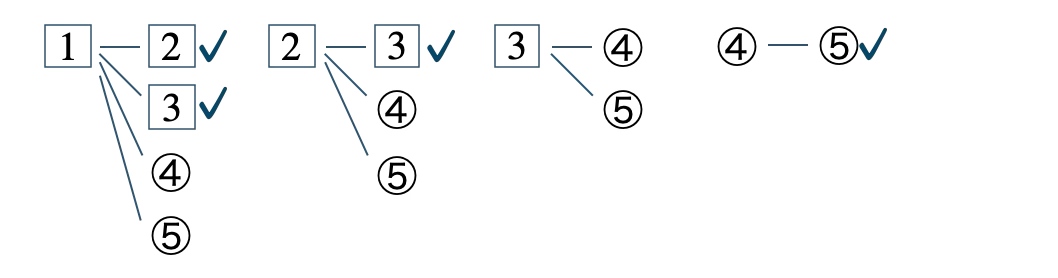
✓を付けた \(4\) 通りであるので、確率は、
\(~~~\displaystyle \frac{\,4\,}{\,10\,}=\displaystyle \frac{\,2\,}{\,5\,}\)
したがって、答えは \({\displaystyle \frac{\,2\,}{\,5\,}}\) となる
問題解説(4)
赤玉3個、白玉2個の入った袋から同時に2個の玉を取り出すとき、次の確率を求めよ。
さらに、この袋に青玉1個を入れて同時に2個の玉を取り出すとき、次の確率を求めよ。
\({\small (4)}~\)赤玉1個と青玉1個を取り出す確率
赤玉3個、白玉2個、青玉1個を、
赤玉3個を \(\fbox{1}\) \(\fbox{2}\) \(\fbox{3}\)、白玉2個を ④ ⑤
青玉1個を 6
と区別して考える
この中から2個を取り出すとき、選ぶだけのパターンとなり樹形図をかくと、
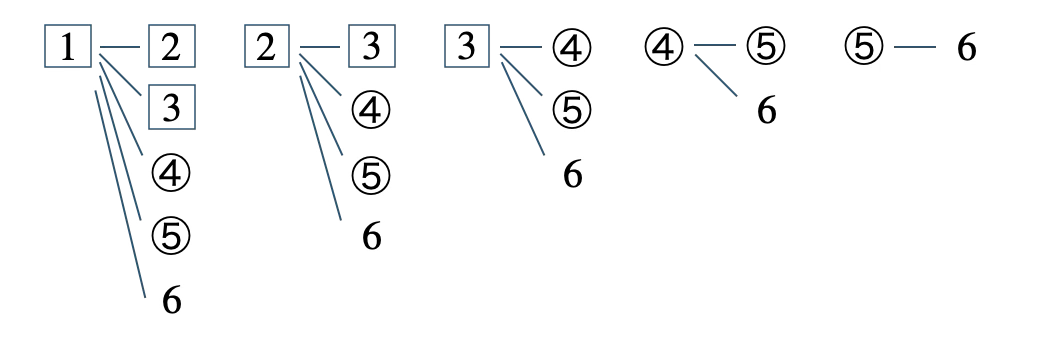
※ \(\fbox{1}\) – \(\fbox{2}\) と \(\fbox{2}\) – \(\fbox{1}\) は同じになるので注意。
これより、すべての場合の数は、
\(~~~5+4+3+2+1=15\)
\(15\) 通りとなり、同様に確からしい
この中で赤玉1個と青玉1個を取り出すのは、
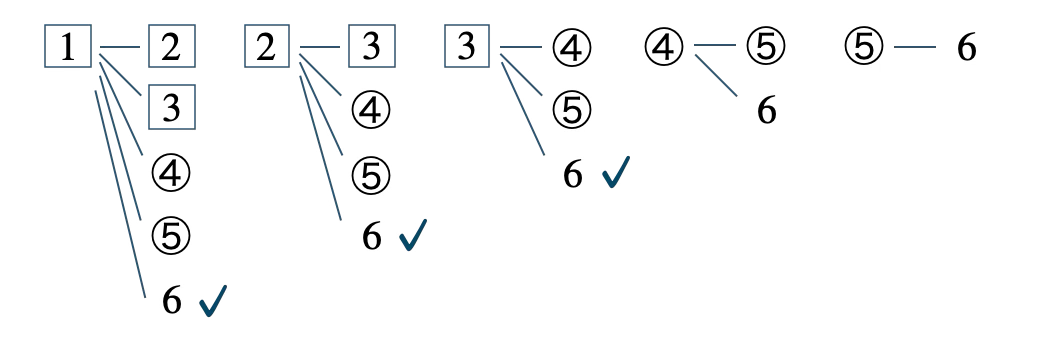
✓を付けた \(3\) 通りであるので、確率は、
\(~~~\displaystyle \frac{\,3\,}{\,15\,}=\displaystyle \frac{\,1\,}{\,5\,}\)
したがって、答えは \({\displaystyle \frac{\,1\,}{\,5\,}}\) となる
問題解説(5)
赤玉3個、白玉2個の入った袋から同時に2個の玉を取り出すとき、次の確率を求めよ。
さらに、この袋に青玉1個を入れて同時に2個の玉を取り出すとき、次の確率を求めよ。
\({\small (5)}~\)違う色の玉を取り出す確率
起こりうるすべての場合の数は \(15\) 通りである
この中で違う色の玉を取り出すのは、
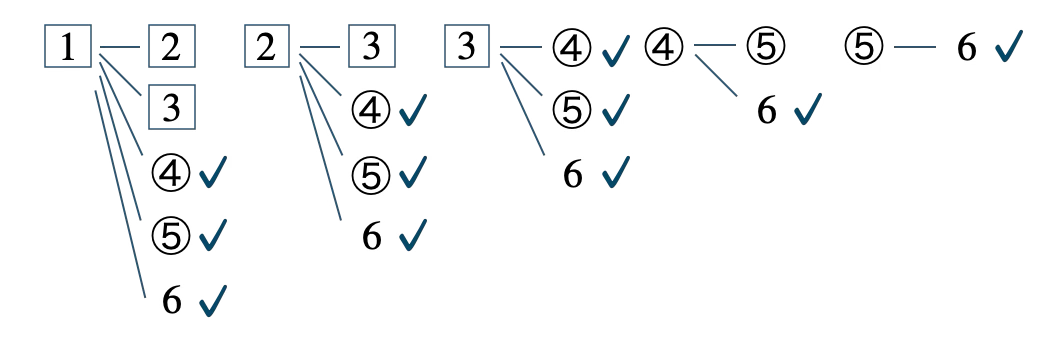
✓を付けた \(11\) 通りである
したがって、確率は \({\displaystyle \frac{\,11\,}{\,15\,}}\) となる
追加の練習問題のページはこちら→
玉を2個同時に取り出す確率|練習問題15問+15問



