四則と計算の順序の解法
Point:四則と計算の順序
\((2^2-1){\, \small \times \,}4+3\)
① 累乗の計算をする。
\(=(4-1){\, \small \times \,}4+3\)
② かっこの中の計算をする。
\(=3{\, \small \times \,}4+3\)
③ 乗法・除法の計算をする。
\(=12+3\)
④ 加法・減法の計算をする。
\(=15\)
四則(加法、減法、乗法、除法)、累乗やかっこ( )が混じった式の計算は、
\((2^2-1){\, \small \times \,}4+3\)
① 累乗の計算をする。
\(=(4-1){\, \small \times \,}4+3\)
② かっこの中の計算をする。
\(=3{\, \small \times \,}4+3\)
③ 乗法・除法の計算をする。
\(=12+3\)
④ 加法・減法の計算をする。
\(=15\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:四則と計算の順序
問題解説(1)
問題
\({\small (1)}~~3+(-2){\, \small \times \,}5\)
次の計算をせよ。
\({\small (1)}~~3+(-2){\, \small \times \,}5\)
加法より乗法の計算を先にする
異なる符号の積なので、
負の符号で、絶対値の積より、
\(\begin{split}&3+(-2){\, \small \times \,}5\\[2pt]~~=~&3-(2{\, \small \times \,}5)\\[2pt]~~=~&3-10\end{split}\)
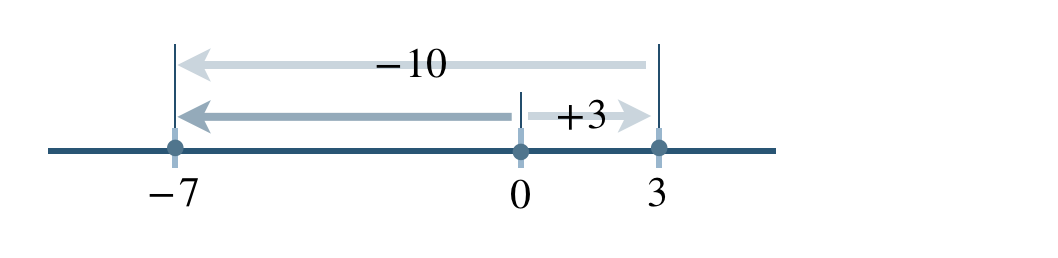
\(\begin{split}~~=~&-(10-3)\\[2pt]~~=~&-7\end{split}\)
したがって、答えは \(-7\) となる
問題解説(2)
問題
\({\small (2)}~~(2-7){\, \small \times \,}(-4)\)
次の計算をせよ。
\({\small (2)}~~(2-7){\, \small \times \,}(-4)\)
かっこの中を先に計算する
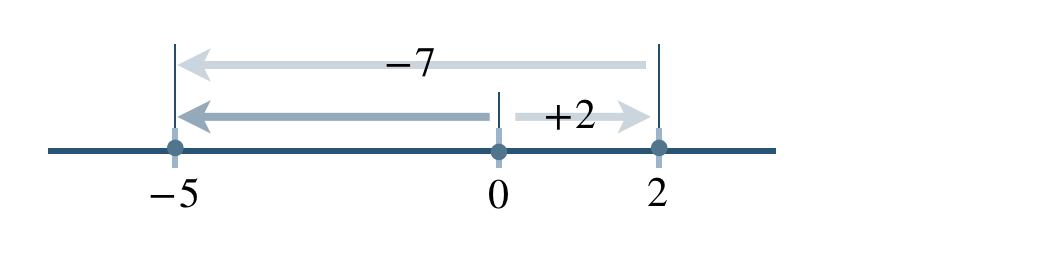
\(\begin{split}&(2-7){\, \small \times \,}(-4)\\[2pt]~~=~&\{-(7-2)\}{\, \small \times \,}(-4)\\[2pt]~~=~&-5{\, \small \times \,}(-4)\end{split}\)
同じ符号の積なので、
正の符号で、絶対値の積より、
\(\begin{split}~~=~&+(5{\, \small \times \,}4)\\[2pt]~~=~&20\end{split}\)
したがって、答えは \(20\) となる
問題解説(3)
問題
\({\small (3)}~~(-18){\, \small \div \,}3-3\)
次の計算をせよ。
\({\small (3)}~~(-18){\, \small \div \,}3-3\)
減法より除法の計算を先にする
異なる符号の商なので、
負の符号で、絶対値の商より、
\(\begin{split}&(-18){\, \small \div \,}3-3\\[2pt]~~=~&-(18{\, \small \div \,}3)-3\\[2pt]~~=~&-6-3\end{split}\)
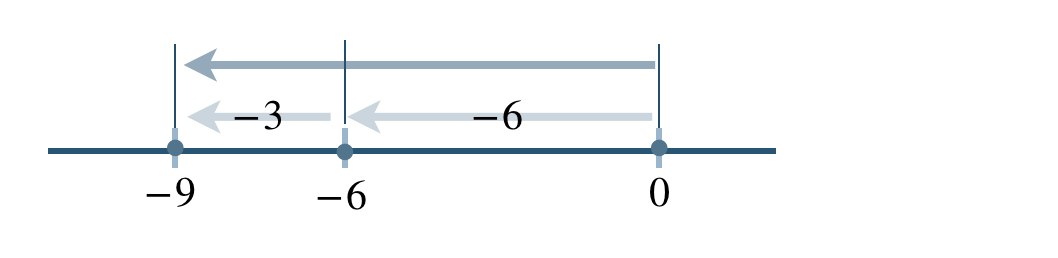
\(\begin{split}&-(6+3)\\[2pt]~~=~&-9\end{split}\)
したがって、答えは \(-9\) となる
問題解説(4)
問題
\({\small (4)}~~24{\, \small \div \,}(1-3^2)\)
次の計算をせよ。
\({\small (4)}~~24{\, \small \div \,}(1-3^2)\)
累乗の計算を先にすると、\(3^2=9\) より、
\(\begin{split}&24{\, \small \div \,}(1-3^2)\\[2pt]~~=~&24{\, \small \div \,}(1-9)\end{split}\)
次に、かっこの中を計算すると、
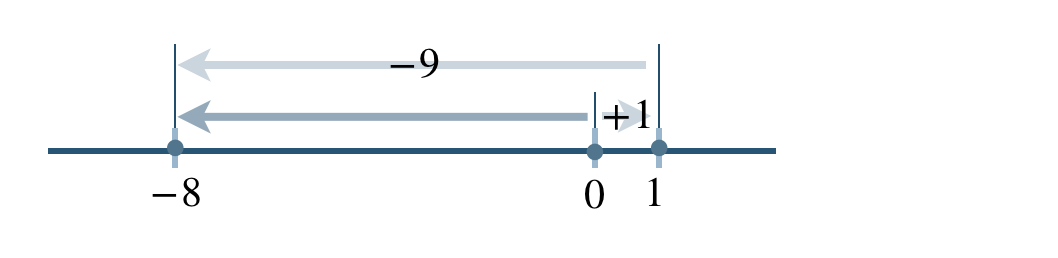
\(\begin{split}~~=~&24{\, \small \div \,}\{-(9-1)\}\\[2pt]~~=~&24{\, \small \div \,}(-8)\end{split}\)
異なる符号の商なので、
負の符号で、絶対値の商より、
\(\begin{split}~~=~&-(24{\, \small \div \,}8)\\[2pt]~~=~&-3\end{split}\)
したがって、答えは \(-3\) となる
問題解説(5)
問題
\({\small (5)}~~2^3{\, \small \times \,}(-3)-35{\, \small \div \,}(-5)\)
次の計算をせよ。
\({\small (5)}~~2^3{\, \small \times \,}(-3)-35{\, \small \div \,}(-5)\)
累乗の計算を先にすると、\(2^3=8\) より、
\(\begin{split}&2^3{\, \small \times \,}(-3)-35{\, \small \div \,}(-5)\\[2pt]~~=~&8{\, \small \times \,}(-3)-35{\, \small \div \,}(-5)\end{split}\)
次に、減法より乗法・除法を先に計算する
異なる符号の積なので、負の符号で、絶対値の積
同じ符号の商なので、正の符号で、絶対値の商より、
\(\begin{split}~~=~&-(8{\, \small \times \,}3)+(35{\, \small \div \,}5)\\[2pt]~~=~&-24+7\end{split}\)
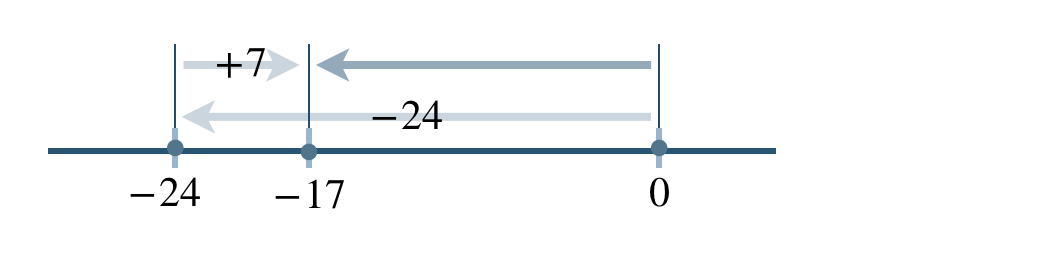
\(\begin{split}~~=~&-(24-7)\\[2pt]~~=~&-17\end{split}\)
したがって、答えは \(-17\) となる
問題解説(6)
問題
\({\small (6)}~~(10^2+2^3){\, \small \div \,}(-3^2)\)
次の計算をせよ。
\({\small (6)}~~(10^2+2^3){\, \small \div \,}(-3^2)\)
累乗の計算を先にすると、
\(10^2=100~,~2^3=8~,~-3^2=-9\) より、
\(\begin{split}&(10^2+2^3){\, \small \div \,}(-3^2)\\[2pt]~~=~&(100+8){\, \small \div \,}(-9)\end{split}\)
次に、かっこの中を計算すると、
\(\begin{split}~~=~&108{\, \small \div \,}(-9)\end{split}\)
異なる符号の商なので、
負の符号で、絶対値の商より、
\(\begin{split}~~=~&-(108{\, \small \div \,}9)\\[2pt]~~=~&-12\end{split}\)
したがって、答えは \(-12\) となる

【問題一覧】中1|正の数と負の数
このページは「中学数学1 正の数と負の数」の問題一覧ページとなります。解説の見たい単元名がわからない...


