数の集まりと四則計算

数の集まりと四則計算の解法

Point：数の集まりと四則計算

■ 数の集まり
　すべての数の中に整数がふくまれていて、
　整数の中に自然数がふくまれている。

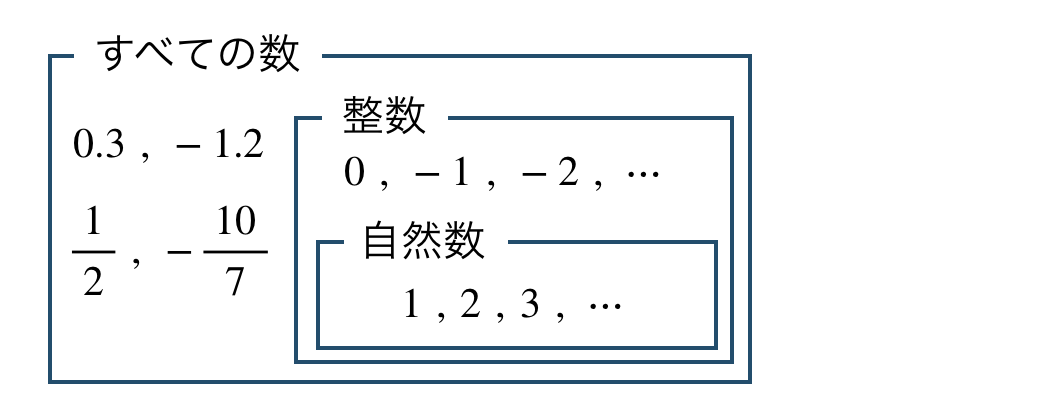
※ これらの集まりを集合という。

■ 数の集まりと四則計算
\({\small (1)}~\)すべての数
　四則計算はいつでもできる

\({\small (2)}~\)整数
　加法、減法、乗法の結果は必ず整数
　ただし、除法はできない

\({\small (3)}~\)自然数
　加法、乗法の結果は必ず自然数
　ただし、減法や除法はできない

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

問題

次の(1)〜(3)の集合の中で、加法、減法、乗法、除法の計算のうち、いつでもできるものをそれぞれ選べ。

\({\small (1)}~\)自然数

自然数どうしの加法は、結果が必ず自然数となる

自然数どうしの減法は、

　　\(3-5=-2\)

このように、結果が自然数とならないことがある

自然数どうしの乗法は、結果が必ず自然数となる

自然数どうしの除法は、

　　\(\begin{split}3{\, \small \div \,}5=\frac{\,3\,}{\,5\,}=0.6\end{split}\)

このように、結果が自然数とならないことがある

したがって、答えは
　いつでもできるのは加法と乗法である

問題

次の(1)〜(3)の集合の中で、加法、減法、乗法、除法の計算のうち、いつでもできるものをそれぞれ選べ。

\({\small (2)}~\)整数

整数どうしの加法は、結果が必ず整数となる

整数どうしの減法は、結果が必ず整数となる
( ※ \(3-5=-2\) のとき \(-2\) は整数である )

整数どうしの乗法は、結果が必ず整数となる

整数どうしの除法は、

　　\(\begin{split}-3{\, \small \div \,}5=-\frac{\,3\,}{\,5\,}=-0.6\end{split}\)

このように、結果が整数とならないことがある

したがって、答えは
　いつでもできるのは加法と減法と乗法である

問題

次の(1)〜(3)の集合の中で、加法、減法、乗法、除法の計算のうち、いつでもできるものをそれぞれ選べ。

\({\small (3)}~\)すべての数

すべての数どうしの四則計算は、いつでもできる

よって、答えは
　いつでもできるのは加法、減法、乗法、除法
である