文字式と図形の解法
Point:文字式と図形
① 単位をそろえる。
\(1~({\rm m})\) = \(100~({\rm cm})\)、\(1~({\rm cm})\) = \(\begin{split}\frac{\,1\,}{\,100\,}~({\rm m})\end{split}\)
② 問題文を図で表す。
③ 長さや面積を文字式で表す。
\({\small (1)}~\)残りの長さ
もとの長さ ー 切り取った長さ = 残りの長さ
\({\small (2)}~\)長方形
周りの長さ = ( たて + よこ )\({\, \small \times \,}\)\(2\)
面積 = たての長さ\({\, \small \times \,}\)よこの長さ
\({\small (3)}~\)円
周りの長さ = 半径\({\, \small \times \,}\)\(2\)\({\, \small \times \,}\)円周率 \(\pi\)
面積 = 半径\({\, \small \times \,}\)半径\({\, \small \times \,}\)円周率 \(\pi\)
※ 円周率は \(3.1415\cdots\) と限りなく続く数なので、文字 \(\pi\) (パイ)を使って表す。また、文字式で表すときは、数学→円周率 \(\pi\) →文字の順で書く。
図形についての問題の文字式での表し方は、
① 単位をそろえる。
\(1~({\rm m})\) = \(100~({\rm cm})\)、\(1~({\rm cm})\) = \(\begin{split}\frac{\,1\,}{\,100\,}~({\rm m})\end{split}\)
② 問題文を図で表す。
③ 長さや面積を文字式で表す。
\({\small (1)}~\)残りの長さ
もとの長さ ー 切り取った長さ = 残りの長さ
\({\small (2)}~\)長方形
周りの長さ = ( たて + よこ )\({\, \small \times \,}\)\(2\)
面積 = たての長さ\({\, \small \times \,}\)よこの長さ
\({\small (3)}~\)円
周りの長さ = 半径\({\, \small \times \,}\)\(2\)\({\, \small \times \,}\)円周率 \(\pi\)
面積 = 半径\({\, \small \times \,}\)半径\({\, \small \times \,}\)円周率 \(\pi\)
※ 円周率は \(3.1415\cdots\) と限りなく続く数なので、文字 \(\pi\) (パイ)を使って表す。また、文字式で表すときは、数学→円周率 \(\pi\) →文字の順で書く。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:文字式と図形
問題解説(1)
問題
\({\small (1)}~\)長さ \(a~({\rm m})\) のひもから、長さ \(b~({\rm cm})\) のひもを切りとった残りの長さ\(({\rm cm})\)。
次の数量を文字式で表せ。
\({\small (1)}~\)長さ \(a~({\rm m})\) のひもから、長さ \(b~({\rm cm})\) のひもを切りとった残りの長さ\(({\rm cm})\)。
\(({\rm cm})\) で単位をそろえる
\(a~({\rm m})\) を \(({\rm cm})\) にすると、
\(\begin{split}a\times100=100a~({\rm cm})\end{split}\)
よって、図で表すと、
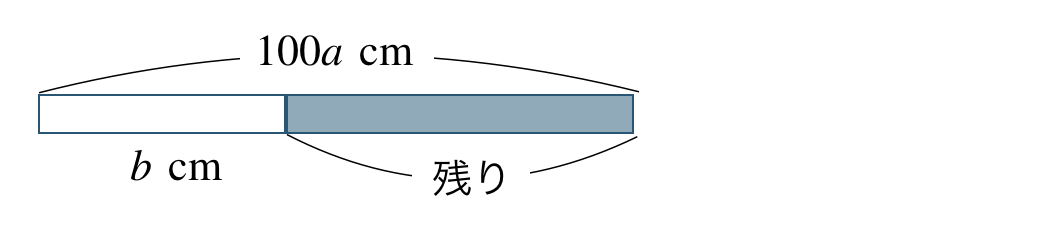
これより、残りの長さを文字式で表すと、
答えは \(100a-b~({\rm cm})\) となる
問題解説(2)
問題
\({\small (2)}~\)長さ \(a~({\rm m})\) のひもから、長さ \(b~({\rm cm})\) のひもを切りとった残りの長さ\(({\rm m})\)。
次の数量を文字式で表せ。
\({\small (2)}~\)長さ \(a~({\rm m})\) のひもから、長さ \(b~({\rm cm})\) のひもを切りとった残りの長さ\(({\rm m})\)。
\(({\rm m})\) で単位をそろえる
\(b~({\rm cm})\) を \(({\rm m})\) にすると、
\(\begin{split}b\times\frac{\,1\,}{\,100\,}=\frac{\,b\,}{\,100\,}~({\rm m})\end{split}\)
よって、図で表すと、
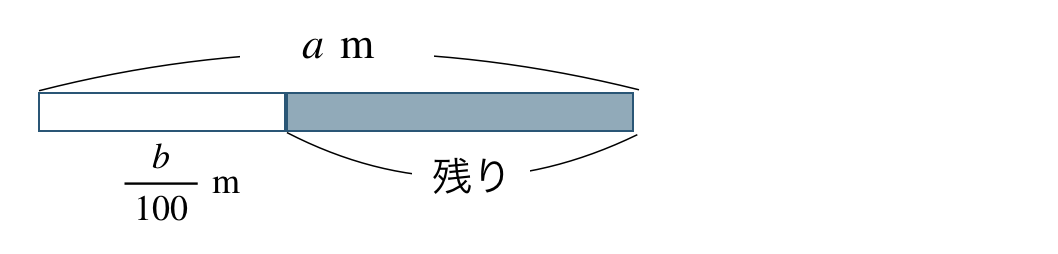
これより、残りの長さを文字式で表すと、
答えは \(\begin{split}a-{\frac{\,b\,}{\,100\,}}~({\rm m})\end{split}\) となる
問題解説(3)
問題
\({\small (3)}~\)1辺の長さ \(x~({\rm cm})\) の正方形の周りの長さ \(({\rm cm})\) と面積 \(({\rm cm}^2)\)。
次の数量を文字式で表せ。
\({\small (3)}~\)1辺の長さ \(x~({\rm cm})\) の正方形の周りの長さ \(({\rm cm})\) と面積 \(({\rm cm}^2)\)。
図で表すと、

周りの長さは「1辺の長さ\({\, \small \times \,}\)\(4\)」より、
\(\begin{split}x\times 4=4x~({\rm cm})\end{split}\)
面積は「たての長さ\({\, \small \times \,}\)よこの長さ」より、
\(\begin{split}x\times x=x^2~({\rm cm}^2)\end{split}\)
したがって、答えは
周りの長さ \(4x~({\rm cm})\)、面積 \(x^2~({\rm cm}^2)\) となる
問題解説(4)
問題
\({\small (4)}~\)半径 \(r~({\rm cm})\) の円の周りの長さ \(({\rm cm})\) と面積 \(({\rm cm}^2)\)。ただし、円周率は \(\pi\) とする。
次の数量を文字式で表せ。
\({\small (4)}~\)半径 \(r~({\rm cm})\) の円の周りの長さ \(({\rm cm})\) と面積 \(({\rm cm}^2)\)。ただし、円周率は \(\pi\) とする。
図で表すと、

円の周りの長さは「半径\({\, \small \times \,}\)\(2\)\({\, \small \times \,}\)円周率」より、
\(\begin{split}r\times 2\times \pi=2\pi r~({\rm cm})\end{split}\)
円の面積は「半径\({\, \small \times \,}\)半径\({\, \small \times \,}\)円周率」より、
\(\begin{split}r\times r\times \pi=\pi r^2~({\rm cm}^2)\end{split}\)
したがって、答えは
円の周りの長さ \(2\pi r~({\rm cm})\)
円の面積 \(\pi r^2~({\rm cm}^2)\)
となる

【問題一覧】中1|文字式
このページは「中学数学1 文字式」の問題一覧ページとなります。解説の見たい単元名がわからないときは、...
12
タイトルとURLをコピーしました


