大小関係を表す式

Point：大小関係を表す式

数量の大小関係を不等号を使って表す式を「不等式」という。

---

不等式 \(2x+3<12\) について、
　\(2x+3\) を左辺、\(12\) を右辺、\(<\) を不等号、
　左辺と右辺を合わせて「両辺」という。

---

■ 大小関係と不等号

---

\({\small (1)}~\)\(x\) が \(a\) より大きい
　記号 \(>\) を使って \(x> a\)
※ 記号 \(<\) を使って \(a< x\) でもよい。

---

\({\small (2)}~\)\(x\) が \(a\) より小さい( \(a\) 未満)
　記号 \(<\) を使って \(x< a\)

---

\({\small (3)}~\)\(x\) が \(a\) 以上　記号 \(≧\) を使って \(x≧a\)

---

\({\small (4)}~\)\(x\) が \(a\) 以下　記号 \(≦\) を使って \(x≦a\)

---

※ 以上や以下では不等号にイコールが付く。

---

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

問題

次の数量の関係を不等式で表す。

---

\({\small (1)}~\)\(x\) と \(y\) の和が \(24\) より大きい。

図で表すと、

\(x\) と \(y\) の和 \(x+y\) より、これが \(24\) より大きいので、

---

答えは、\(x+y>24\) となる

問題

次の数量の関係を不等式で表す。

---

\({\small (2)}~\)\(x\) と \(y\) の積が \(10\) 以下となる。

図で表すと、

\(x\) と \(y\) の積 \(x{\, \small \times \,} y=xy\) より、これが \(10\) 以下なので、

---

答えは、\(xy≦10\) となる

問題

次の数量の関係を不等式で表す。

---

\({\small (3)}~\)１個 \(a~({\rm g})\) のみかん３個と１個 \(b~({\rm g})\) のりんご５個の合計の重さが \(1.8~({\rm kg})\) 以上である。

図で表すと、

\(1.8~({\rm kg})\) を \({\rm g}\) にすると、

---

　\(1.8{\, \small \times \,}1000=1800~({\rm g})\)

---

１個 \(a~({\rm g})\) のみかん３個と１個 \(b~({\rm g})\) のりんご５個の合計の重さは、

---

　\(a{\, \small \times \,} 3+b{\, \small \times \,} 5=3a+5b~({\rm g})\)

---

これが \(1800\) 以上となるので、

---

答えは、\(3a+5b≧1800\) となる

問題

次の数量の関係を不等式で表す。

---

\({\small (4)}~\)\(a\) ページの本を１日に \(b\) ページ読んだが \(10\) 日で読み終わらなかった。

図で表すと、

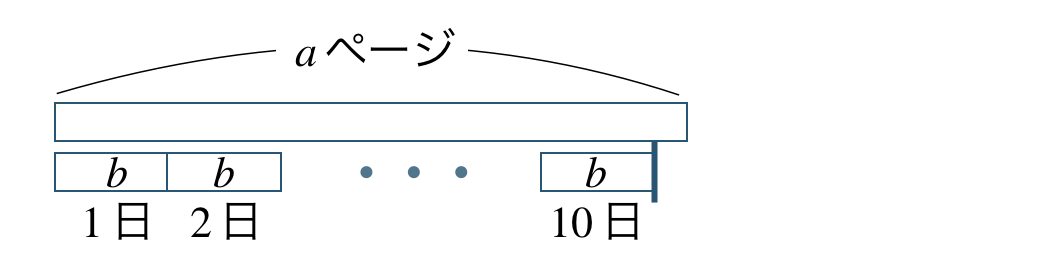
１日に \(b\) ページ読むのを \(10\) 日続けると、

---

　\(b{\, \small \times \,} 10=10b\)

---

これが \(a\) ページより小さい(\(a\) ページ未満)であるので、

---

答えは、\(10b< a\) となる