1次方程式と過不足の解法
Point:1次方程式と過不足
① 求める値を \(x\) とおく。
② 過不足を図で表し、図より1次方程式を立てる。
たとえば、みかんを子どもに分けるとき、
\(1\) 人 \(2\) 個ずつ分けると \(3\) 個余り
\(1\) 人 \(3\) 個ずつ分けると \(2\) 個たりない
子どもの人数を \(x\) 人とすると、
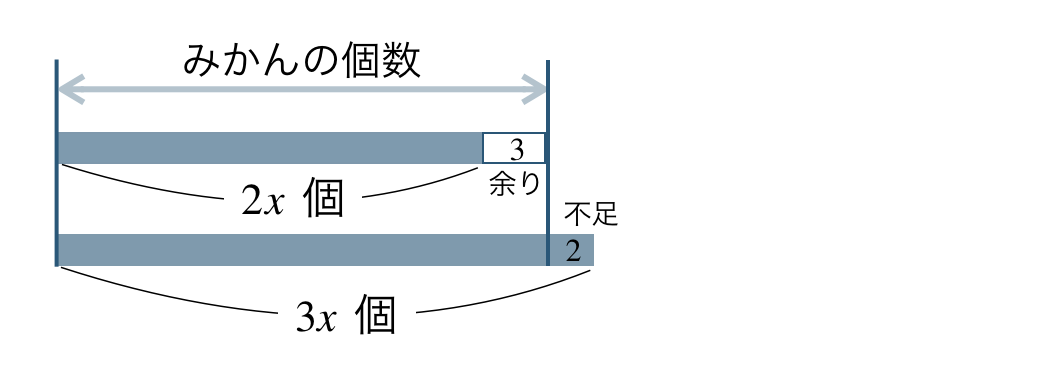
これより、みかんの個数で等式を立てると、
\(~~~2x+3=3x-2\)
③ 立てた1次方程式を解く。
④ 解が問題に適しているか確かめる。
過不足のある文章問題は、
① 求める値を \(x\) とおく。
② 過不足を図で表し、図より1次方程式を立てる。
たとえば、みかんを子どもに分けるとき、
\(1\) 人 \(2\) 個ずつ分けると \(3\) 個余り
\(1\) 人 \(3\) 個ずつ分けると \(2\) 個たりない
子どもの人数を \(x\) 人とすると、

これより、みかんの個数で等式を立てると、
\(~~~2x+3=3x-2\)
③ 立てた1次方程式を解く。
④ 解が問題に適しているか確かめる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:1次方程式と過不足
問題解説(1)
問題
\({\small (1)}~\)子どもの人数を \(x\) 人として求める。
何人かの子どもにアメを同じ数だけ配る。
\(1\) 人 \(5\) 個ずつ配ると \(14\) 個余り
\(1\) 人 \(7\) 個ずつ配ると \(6\) 個たりない
このとき、子どもの人数とアメの個数を求めよ。
\({\small (1)}~\)子どもの人数を \(x\) 人として求める。
子どもの人数を \(x\) 人とすると、
\(5\) 個ずつ配ると \(5x\) 個必要で、\(14\) 個余る
\(7\) 個ずつ配ると \(7x\) 個必要で、\(6\) 個たりない
これより、
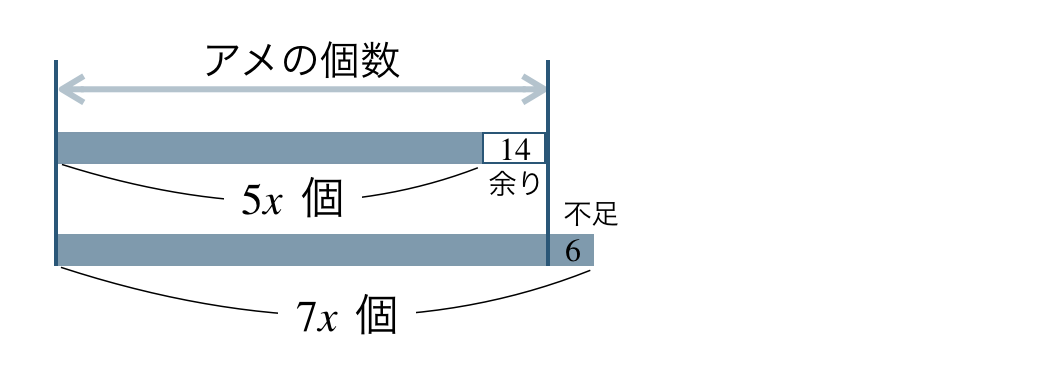
アメの個数は、
\(5\) 個ずつ配るとき、\(5x+14\)
\(7\) 個ずつ配るとき、\(7x-6\)
となるので、1次方程式を立てると、
\(\begin{split}\hspace{3pt}~~~5x+14=7x-6\end{split}\)
\(14\) と \(7x\) をそれぞれ移項すると、符号がかわるので、
\(\begin{eqnarray}\hspace{3pt}~~~5x-7x&=&-6-14\\[2pt]~~~(5-7)x&=&-20\\[2pt]~~~-2x&=&-20\end{eqnarray}\)
両辺を \(x\) の係数 \(-2\) でわると、
\(\require{cancel} \begin{eqnarray}~~~\frac{\,-2x\,}{\,-2\,}&=&\frac{\,-20\,}{\,-2\,}\\[2pt]~~~\frac{\,\cancel{-2}^{1}x\,}{\,\cancel{-2}^{1}\,}&=&\frac{\,\cancel{-20}^{10}\,}{\,\cancel{-2}^{1}\,}\\[2pt]~~~x&=&10\end{eqnarray}\)
アメの個数は \(5x+14\) 個より、\(x=10\) を代入すると、※ \(7x-6\) に代入してもよい。
\(~~~5{\, \small \times \,}10+14=50+14=64\)
これは問題に適している
したがって、
子ども \(10\) 人、アメ \(64\) 個
となる
問題解説(2)
問題
\({\small (2)}~\)アメの個数を \(x\) 個として求める。
何人かの子どもにアメを同じ数だけ配る。
\(1\) 人 \(5\) 個ずつ配ると \(14\) 個余り
\(1\) 人 \(7\) 個ずつ配ると \(6\) 個たりない
このとき、子どもの人数とアメの個数を求めよ。
\({\small (2)}~\)アメの個数を \(x\) 個として求める。
アメの個数を \(x\) 個とすると、
(子どもの人数)
=(配ったアメの数) ÷ (\(1\) 人に配る個数)
\(1\) 人 \(5\) 個ずつ配ると \(14\) 個余るので、配ったアメの個数は \(x-14\) 個
よって、子どもの人数は、
\(\begin{split}~~~(x-14){\, \small \div \,}5=\frac{\,x-14\,}{\,5\,}\end{split}\)
\(1\) 人 \(7\) 個ずつ配ると \(6\) 個たりないので、配るために必要なアメの個数は \(x+6\) 個
よって、子どもの人数は、
\(\begin{split}~~~(x+6){\, \small \div \,}7=\frac{\,x+6\,}{\,7\,}\end{split}\)
これより、1次方程式を立てると、
\(\begin{split}\hspace{29pt}~~~\frac{\,x-14\,}{\,5\,}=\frac{\,x+6\,}{\,7\,}\end{split}\)
両辺を \(5\) と \(7\) の最小公倍数 \(35\) をかけると、
\(\require{cancel} \begin{eqnarray}~~~\frac{\,x-14\,}{\,5\,}{\, \small \times \,}35&=&\frac{\,x+6\,}{\,7\,}{\, \small \times \,}35\\[3pt]~~~\frac{\,x-14\,}{\,\cancel{5}^{1}\,}{\, \small \times \,}\cancel{35}^{7}&=&\frac{\,x+6\,}{\,\cancel{7}^{1}\,}{\, \small \times \,}\cancel{35}^{5}\\[3pt]~~~(x-14){\, \small \times \,}7&=&(x+6){\, \small \times \,}5\\[2pt]~~~x{\, \small \times \,}7 -14{\, \small \times \,}7&=&x{\, \small \times \,}5+6{\, \small \times \,}5\\[2pt]~~~7x-98&=&5x+30\end{eqnarray}\)
\(-98\) と \(5x\) をそれぞれ移項すると、符号がかわるので、
\(\begin{eqnarray}\hspace{29pt}~~~7x-5x&=&30+98\\[2pt]~~~(7-5)x&=&128\\[2pt]~~~2x&=&128\end{eqnarray}\)
両辺を \(x\) の係数 \(2\) でわると、
\(\require{cancel} \begin{eqnarray}~~~\frac{\,2x\,}{\,2\,}&=&\frac{\,128\,}{\,2\,}\\[2pt]\hspace{33pt}~~~\frac{\,\cancel{2}^{1}x\,}{\,\cancel{2}^{1}\,}&=&\frac{\,\cancel{128}^{64}\,}{\,\cancel{2}^{1}\,}\\[2pt]~~~x&=&64\end{eqnarray}\)
子どもの人数は \(\begin{split}{\frac{\,x-14\,}{\,5\,}}\end{split}\) 人より、\(x=64\) を代入すると、
※ \(\begin{split}{\frac{\,x+6\,}{\,7\,}}\end{split}\) に代入してもよい。
\(\begin{split}~~~\frac{\,64-14\,}{\,5\,}=\frac{\,10\,}{\,5\,}=10\end{split}\)
これは問題に適している
したがって、
子ども \(10\) 人、アメ \(64\) 個
となる

【問題一覧】中1|1次方程式
このページは「中学数学1 1次方程式」の問題一覧ページとなります。解説の見たい単元名がわからないとき...


