このページは「中学数学1 比例と反比例」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう!
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。
【問題一覧】中学数学1 比例と反比例
変数と関数
次の問いに答えよ。
\({\small (1)}~\)次の①〜⑥のうち、\(y\) が \(x\) の関数であるものを答えよ。
① 半径 \(x~{\rm cm}\) の円の面積が \(y~{\rm cm}^2\)。
② \(20~{\rm km}\) の道のりを時速 \(x~{\rm km}\) で走ると \(y\) 時間かかる。
③ \(x\) 歳の人の身長は \(y~{\rm cm}\)。
④ 周の長さ \(20~{\rm cm}\) の長方形の縦の長さ \(x~{\rm cm}\) と横の長さ \(y~{\rm cm}\)。
⑤ 整数 \(x\) の絶対値が \(y\)。
⑥ 周りの長さ \(x~{\rm cm}\) の長方形の面積が \(y~{\rm cm}^2\)。
\({\small (2)}~\)深さ \(30~{\rm cm}\) の空の水そうに \(1\) 分間で高さが \(5~{\rm cm}\) 高くなるように水を入れる。水を入れはじめてから \(x\) 分後の水の高さ \(y~{\rm cm}\) の関係の表を完成させよ。
| \(x\) 分 | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| \(y~{\rm cm}\) | \(5\) |
[ 解答を見る ]
【解答】
\({\small (1)}~\)\(y\) が \(x\) の関数であるものは、① ② ④ ⑤
\({\small (2)}~\)
| \(x\) 分 | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) |
| \(y~{\rm cm}\) | \(5\) | \(10\) | \(15\) | \(20\) | \(25\) | \(30\) |

変域の表し方
次の \(x\) の変域を不等号を使って表せ。
\({\small (1)}~x\) が \(3\) 以上。
\({\small (2)}~x\) が \(-2\) より小さい。
\({\small (3)}~x\) が \(-1\) 以上 \(4\) 以下。
\({\small (4)}~x\) が \(-5\) より大きく \(0\) 以下。
\({\small (5)}~x\) が \(3\) 以上 \(7\) 未満。
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~x≧3\end{split}\)
\(\begin{split}{\small (2)}~x<-2\end{split}\)
\(\begin{split}{\small (3)}~-1≦x≦4\end{split}\)
\(\begin{split}{\small (4)}~-5<x≦0\end{split}\)
\(\begin{split}{\small (5)}~3≦x<7\end{split}\)

比例の関係
次の問いに答えよ。
\({\small (1)}~\)\(1\) 本 \(80\) 円のえんぴつを \(x\) 本買ったときの代金 \(y\) 円について、\(y\) が \(x\) に比例することを示し、比例定数を答え、表を完成させよ。
| \(x\) 本 | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(\cdots\) |
| \(y\) 円 | \(80\) | \(\cdots\) |
\({\small (2)}~\)底辺 \(12~{\rm cm}\)、高さ \(x~{\rm cm}\) の三角形の面積 \(y~{\rm cm}^2\) について、\(y\) が \(x\) に比例することを示し、比例定数を答え、表を完成させよ。
| \(x~{\rm cm}\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(\cdots\) |
| \(y~{\rm cm}^2\) | \(\cdots\) |
\({\small (3)}~\)\(y=-3x\) について、比例定数を答え、表を完成させよ。
| \(x\) | \(\cdots\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(\cdots\) |
| \(y\) | \(\cdots\) | \(\cdots\) |
[ 解答を見る ]
【解答】
\({\small (1)}~\)\(y\) が \(x\) に比例して、比例定数は \(80\)
| \(x\) 本 | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(\cdots\) |
| \(y\) 円 | \(80\) | \(160\) | \(240\) | \(320\) | \(400\) | \(\cdots\) |
\({\small (2)}~\)\(y\) が \(x\) に比例して、比例定数は \(6\)
| \(x~{\rm cm}\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(\cdots\) |
| \(y~{\rm cm}^2\) | \(6\) | \(12\) | \(18\) | \(24\) | \(30\) | \(\cdots\) |
\({\small (3)}~\)比例定数は \(-3\)
| \(x\) | \(\cdots\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(\cdots\) |
| \(y\) | \(\cdots\) | \(6\) | \(3\) | \(0\) | \(-3\) | \(-6\) | \(\cdots\) |

比例の式
次の \(x\) と \(y\) の関係を式で表せ。
\({\small (1)}~\)\(y\) は \(x\) に比例し、\(x=5\) のとき \(y=15\) である。
\({\small (2)}~\)\(y\) は \(x\) に比例し、\(x=-3\) のとき \(y=18\) である。
\({\small (3)}~\)\(y\) は \(x\) に比例し、\(x=-9\) のとき \(y=-6\) である。
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~y=3x\end{split}\)
\(\begin{split}{\small (2)}~y=-6x\end{split}\)
\(\begin{split}{\small (3)}~y=\frac{\,2\,}{\,3\,}x\end{split}\)

座標と点の表し方
次の問いに答えよ。
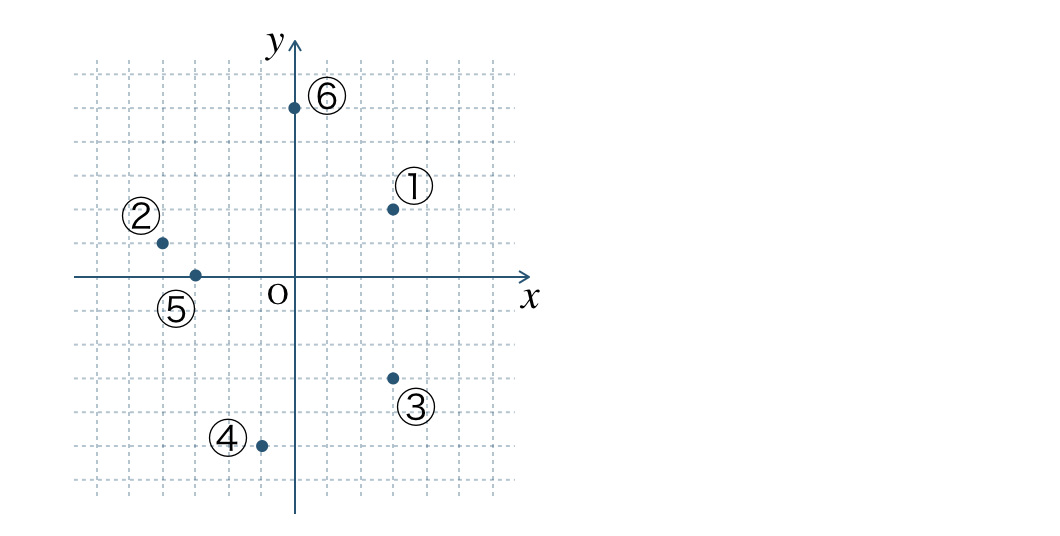
\({\small (1)}~\)次の点①〜⑥の座標を答えよ。
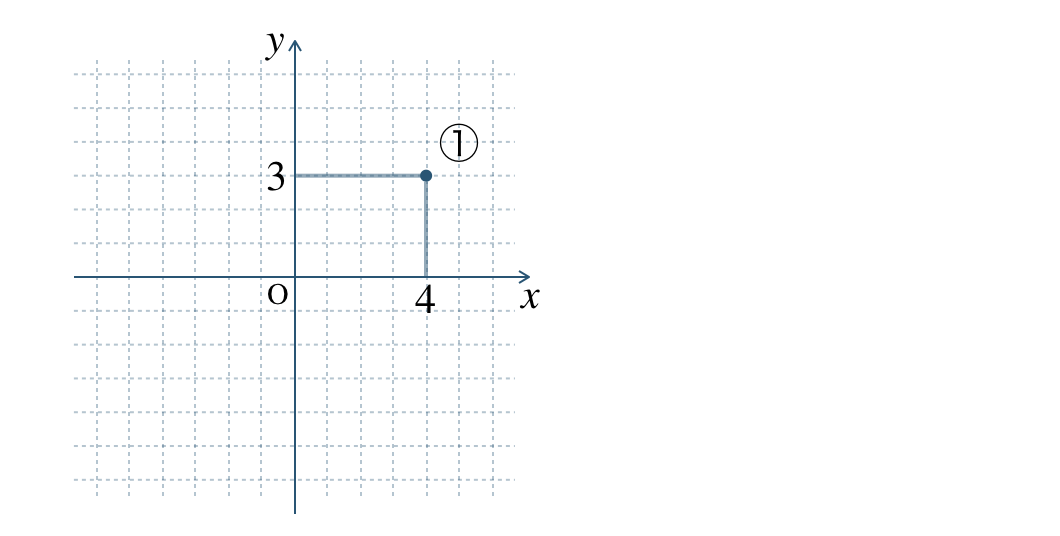
\({\small (2)}~\)次の点を図にかき入れよ。
① \(\begin{split}(4~,~3)\end{split}\)
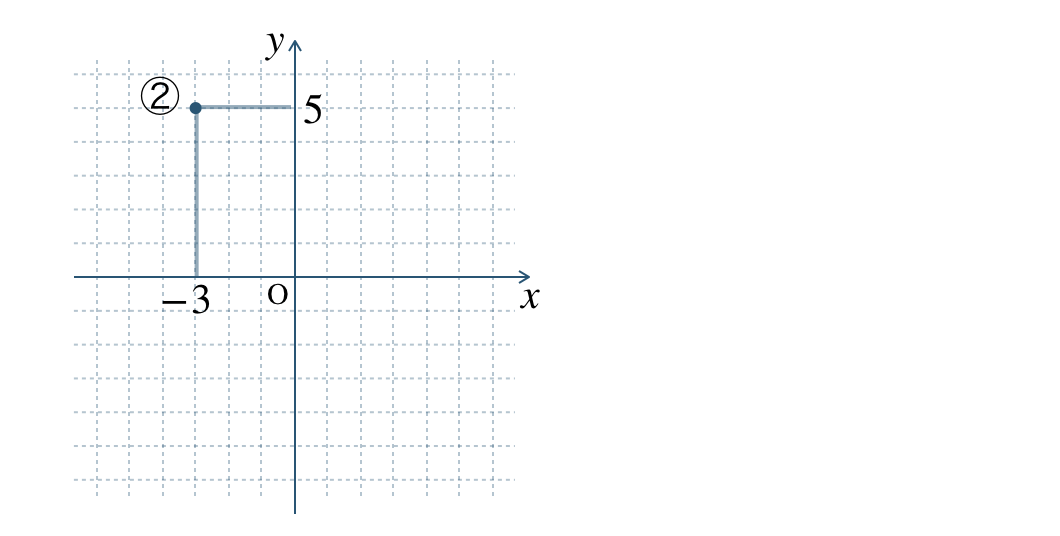
② \(\begin{split}(-3~,~5)\end{split}\)
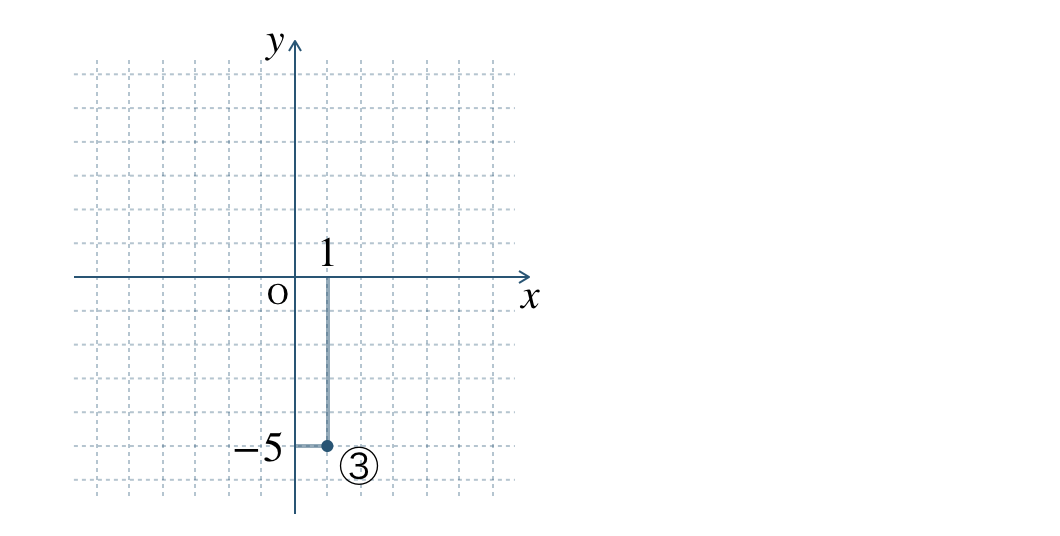
③ \(\begin{split}(1~,~-5)\end{split}\)
④ \(\begin{split}(-2~,~-4)\end{split}\)
⑤ \(\begin{split}(3~,~0)\end{split}\)
⑥ \(\begin{split}(0~,~-2)\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)
① \(\begin{split}(3~,~2)\end{split}\)
② \(\begin{split}(-4~,~1)\end{split}\)
③ \(\begin{split}(3~,~-3)\end{split}\)
④ \(\begin{split}(-1~,~-5)\end{split}\)
⑤ \(\begin{split}(-3~,~0)\end{split}\)
⑥ \(\begin{split}(0~,~5)\end{split}\)
\({\small (2)}~\)
①
②
③
④
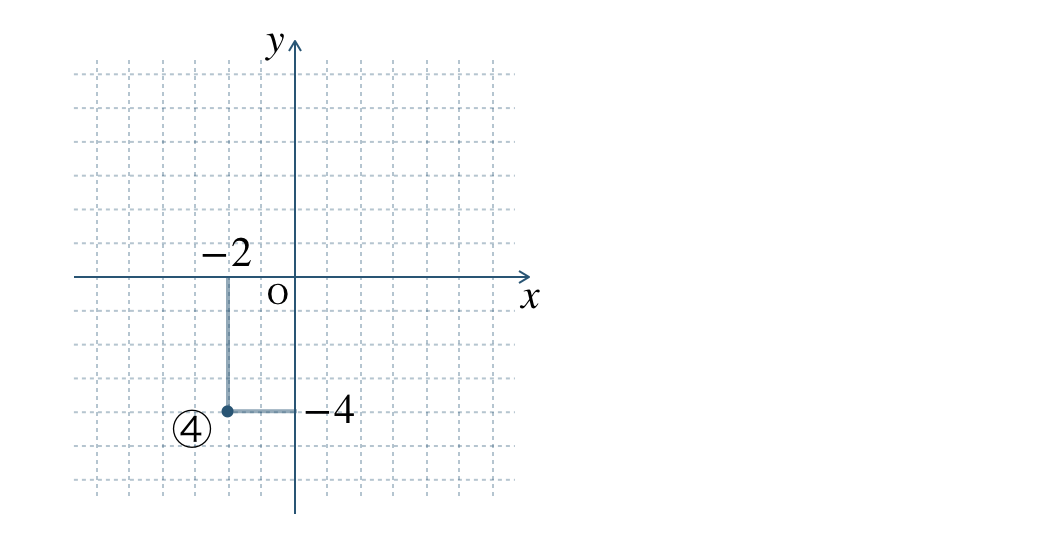
⑤
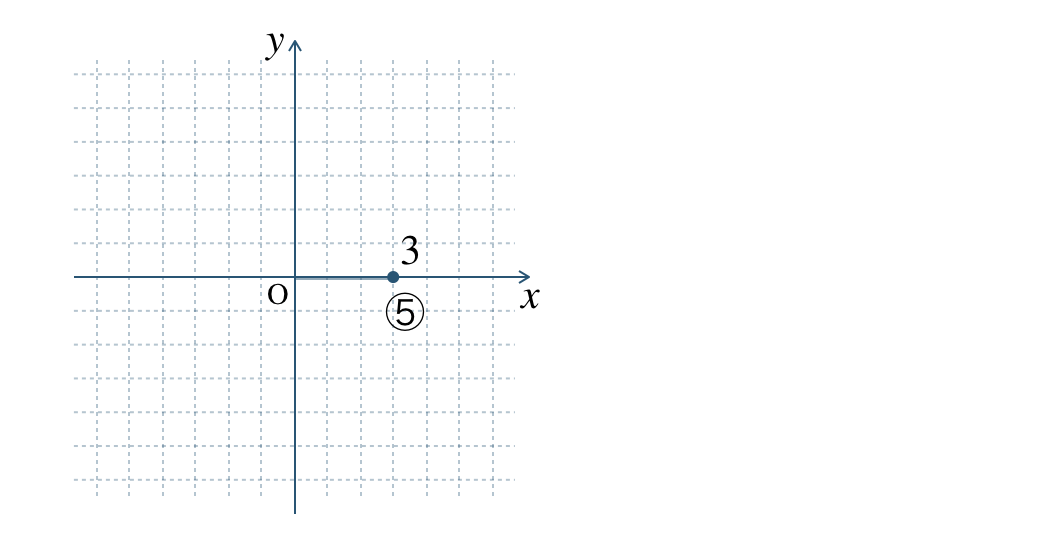
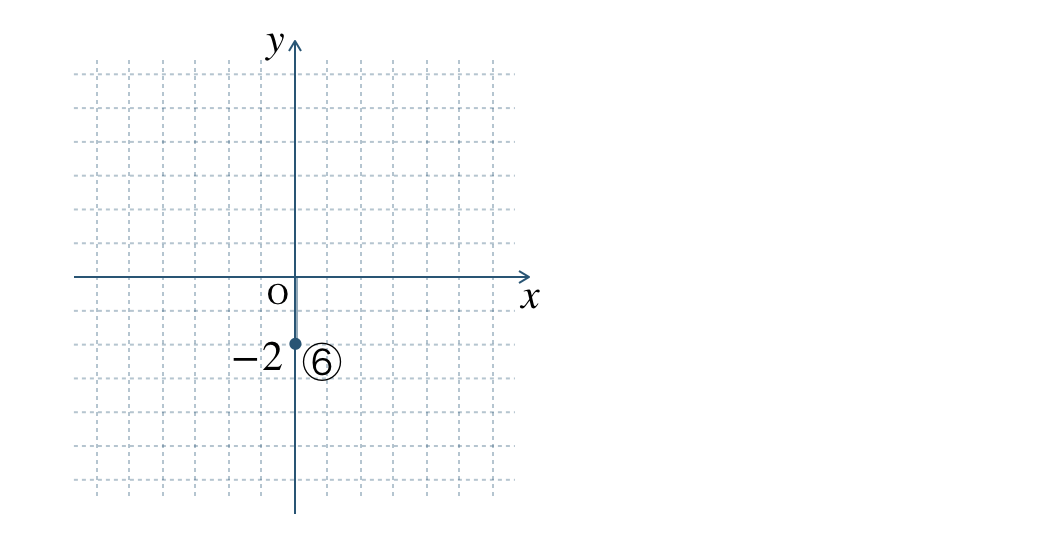
⑥

比例のグラフ
次の比例のグラフをかき、\(x\) が増加するとき \(y\) はどうなるか答えよ。また、グラフは右上がりか右下がりか答えよ。
\(\begin{split}{\small (1)}~y=2x\end{split}\)
\(\begin{split}{\small (2)}~y=-3x\end{split}\)
\(\begin{split}{\small (3)}~y=\frac{\,1\,}{\,2\,}x\end{split}\)
\(\begin{split}{\small (4)}~y=-\frac{\,2\,}{\,3\,}x\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)\(x\) が増加するとき \(y\) も増加して、右上がりのグラフとなる
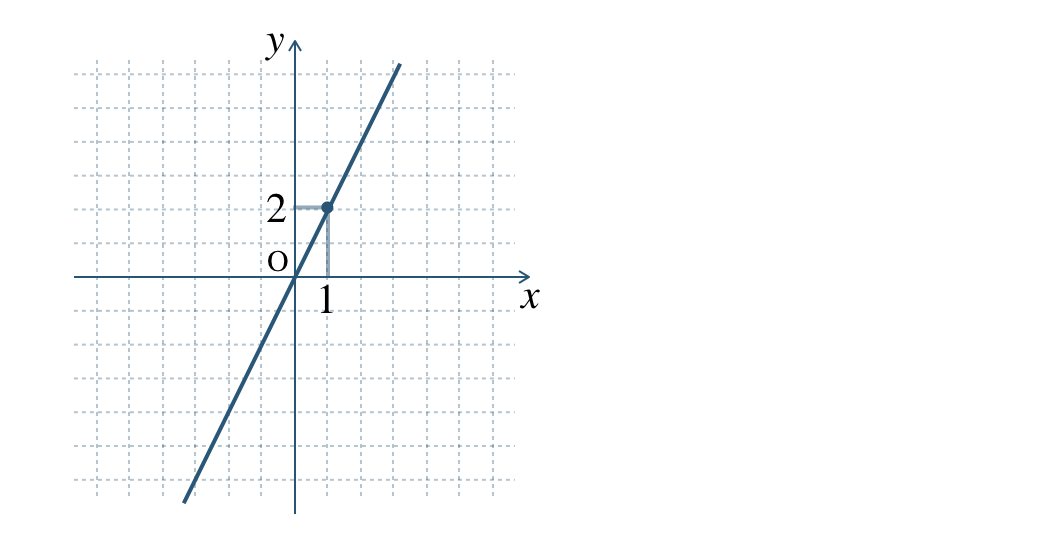
\({\small (2)}~\)\(x\) が増加するとき \(y\) は減少して、右下がりのグラフとなる
\({\small (3)}~\)\(x\) が増加するとき \(y\) も増加して、右上がりのグラフとなる
\({\small (4)}~\)\(x\) が増加するとき \(y\) は減少して、右下がりのグラフとなる

反比例の関係
次の問いに答えよ。
\({\small (1)}~\)縦の長さ \(x~{\rm cm}\)、横の長さ \(y~{\rm cm}\) の三角形の面積が \(6~{\rm cm}^2\) であった。\(y\) が \(x\) に反比例することを示し、比例定数を答え、表を完成させよ。
| \(x~{\rm cm}\) | \(1\) | \(2\) | \(3\) | \(4\) | \(6\) | \(12\) |
| \(y~{\rm cm}\) |
\({\small (2)}~\)\(15~{\rm km}\) の道のりを時速 \(x~{\rm km}\) で進んだとき \(y\) 時間かかった。\(y\) が \(x\) に反比例することを示し、比例定数を答え、表を完成させよ。
| 時速 \(x~{\rm km}\) | \(1\) | \(2\) | \(3\) | \(5\) | \(6\) | \(10\) | \(\cdots\) |
| \(y\) 時間 | \(\cdots\) |
\({\small (3)}~\)\(\begin{split}y=-{\frac{\,4\,}{\,x\,}}\end{split}\) について、比例定数を答え、表を完成させよ。
| \(x\) | \(\cdots\) | \(-4\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(4\) | \(\cdots\) |
| \(y\) | \(\cdots\) | × | \(\cdots\) |
[ 解答を見る ]
【解答】
\({\small (1)}~\)\(y\) が \(x\) に反比例して、比例定数は \(12\)
| \(x~{\rm cm}\) | \(1\) | \(2\) | \(3\) | \(4\) | \(6\) | \(12\) |
| \(y~{\rm cm}\) | \(12\) | \(6\) | \(4\) | \(3\) | \(2\) | \(1\) |
\({\small (2)}~\)\(y\) が \(x\) に反比例して、比例定数は \(15\)
| 時速 \(x~{\rm km}\) | \(1\) | \(2\) | \(3\) | \(5\) | \(6\) | \(10\) | \(\cdots\) |
| \(y\) 時間 | \(15\) | \(7.5\) | \(5\) | \(3\) | \(2.5\) | \(1.5\) | \(\cdots\) |
\({\small (3)}~\)比例定数は \(-4\) となる
| \(x\) | \(\cdots\) | \(-4\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(4\) | \(\cdots\) |
| \(y\) | \(\cdots\) | \(1\) | \(2\) | \(4\) | × | \(-4\) | \(-2\) | \(-1\) | \(\cdots\) |

反比例の式
次の \(x\) と \(y\) の関係を式で表せ。
\({\small (1)}~\)\(y\) は \(x\) に反比例し、\(x=5\) のとき \(y=2\) である。
\({\small (2)}~\)\(y\) は \(x\) に反比例し、\(x=-3\) のとき \(y=2\) である。
\({\small (3)}~\)\(y\) は \(x\) に反比例し、\(x=2\) のとき \(y=-8\) である。
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~y=\frac{\,10\,}{\,x\,}\end{split}\)
\(\begin{split}{\small (2)}~y=-\frac{\,6\,}{\,x\,}\end{split}\)
\(\begin{split}{\small (3)}~y=-\frac{\,16\,}{\,x\,}\end{split}\)

反比例のグラフ
次の反比例のグラフかけ。
\(\begin{split}{\small (1)}~y=\frac{\,6\,}{\,x\,}\end{split}\)
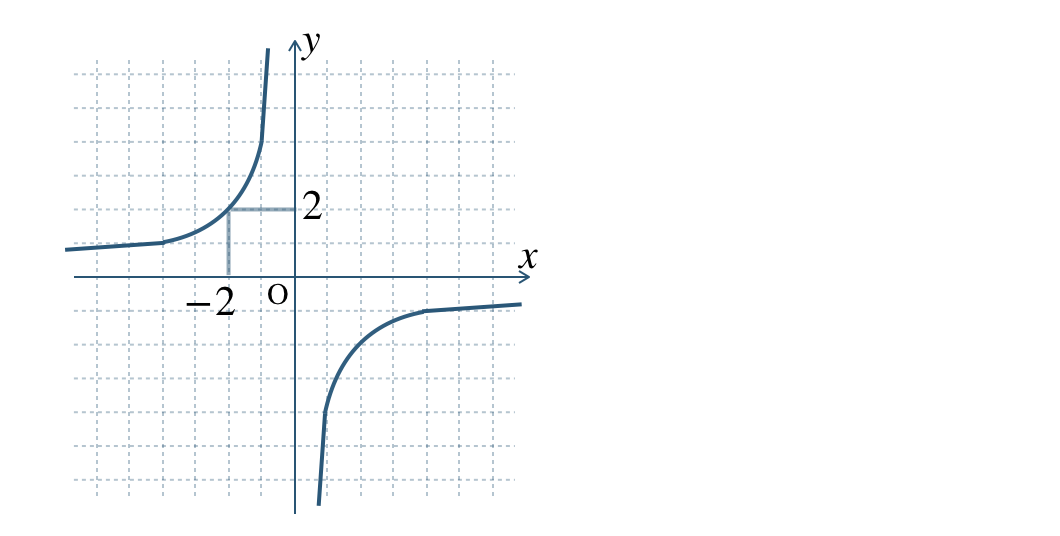
\(\begin{split}{\small (2)}~y=-\frac{\,6\,}{\,x\,}\end{split}\)
\(\begin{split}{\small (3)}~y=-\frac{\,4\,}{\,x\,}\end{split}\)
[ 解答を見る ]
【解答】
\({\small (1)}~\)
\({\small (2)}~\)
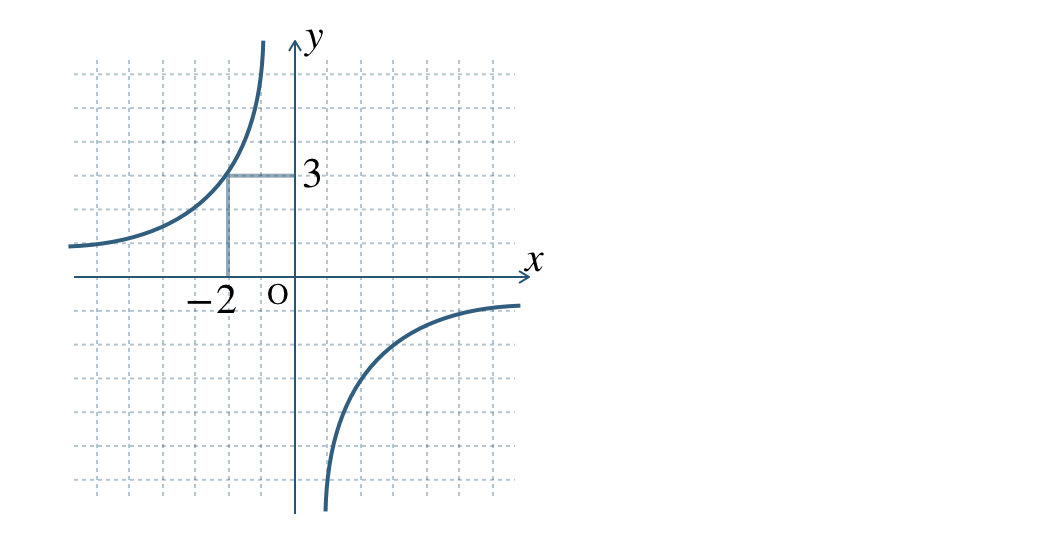
\({\small (3)}~\)

グラフと比例・反比例の式
次の問いに答えよ。
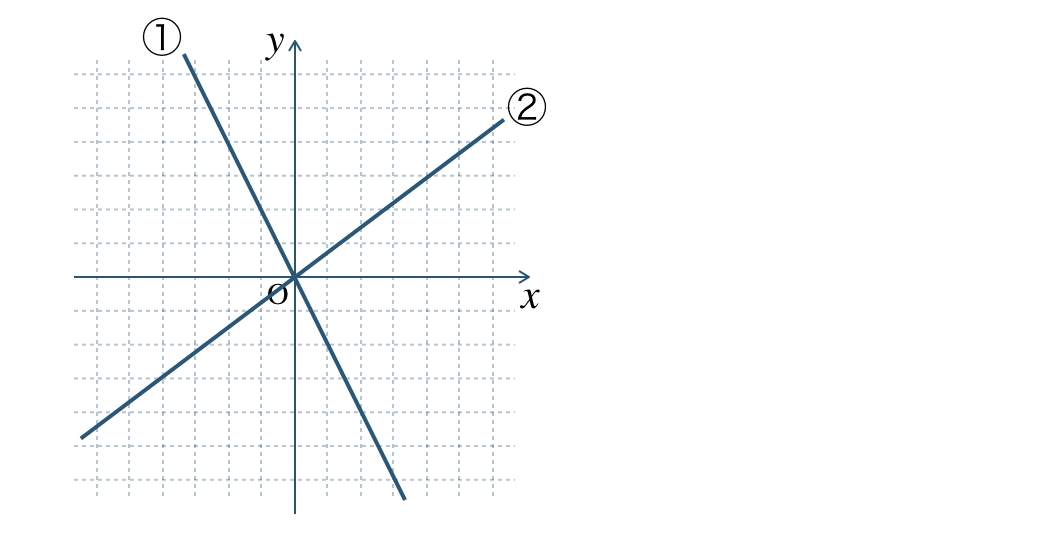
\({\small (1)}~\)次の①と②の直線のグラフを \(y\) を \(x\) の式で表せ。
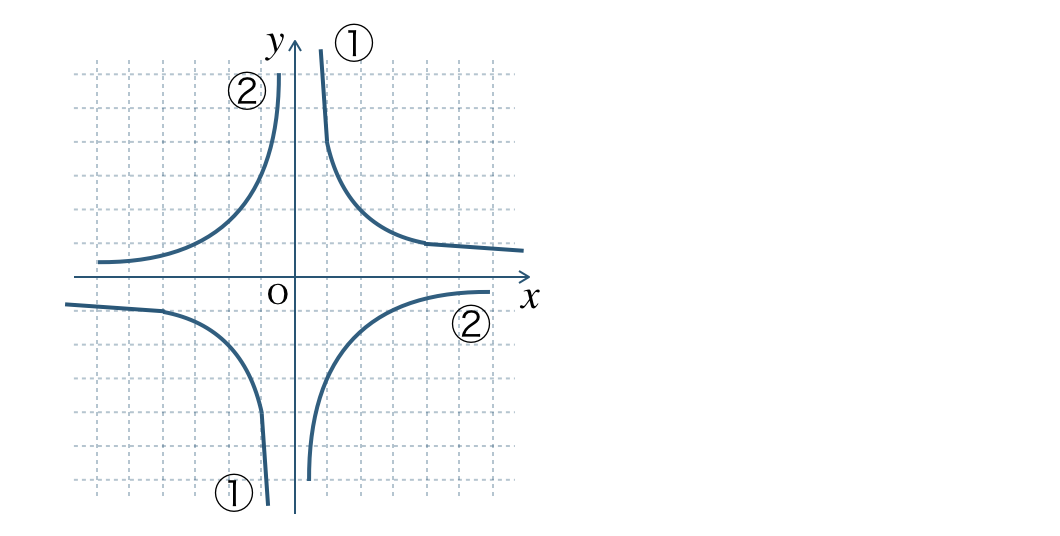
\({\small (2)}~\)次の①と②の双曲線のグラフを \(y\) を \(x\) の式で表せ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
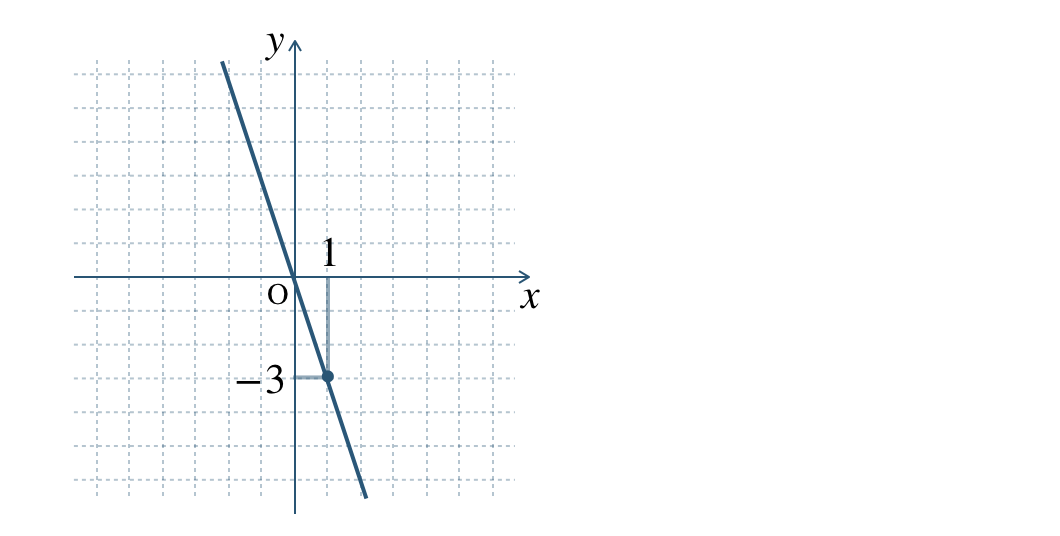
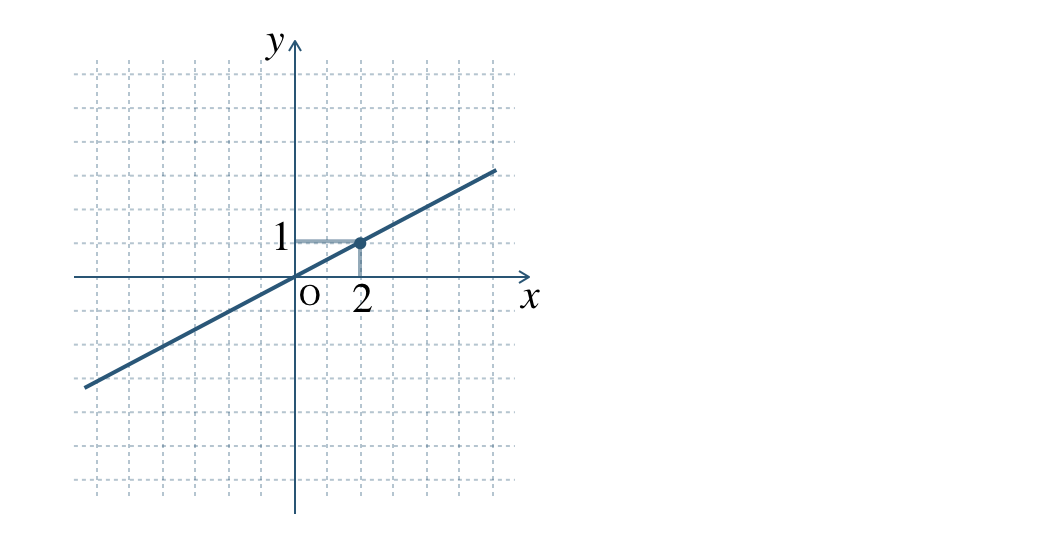
① \(\begin{split}y=-2x\end{split}\) ② \(\begin{split}y=\frac{\,3\,}{\,4\,}x\end{split}\)
\({\small (2)}~\)
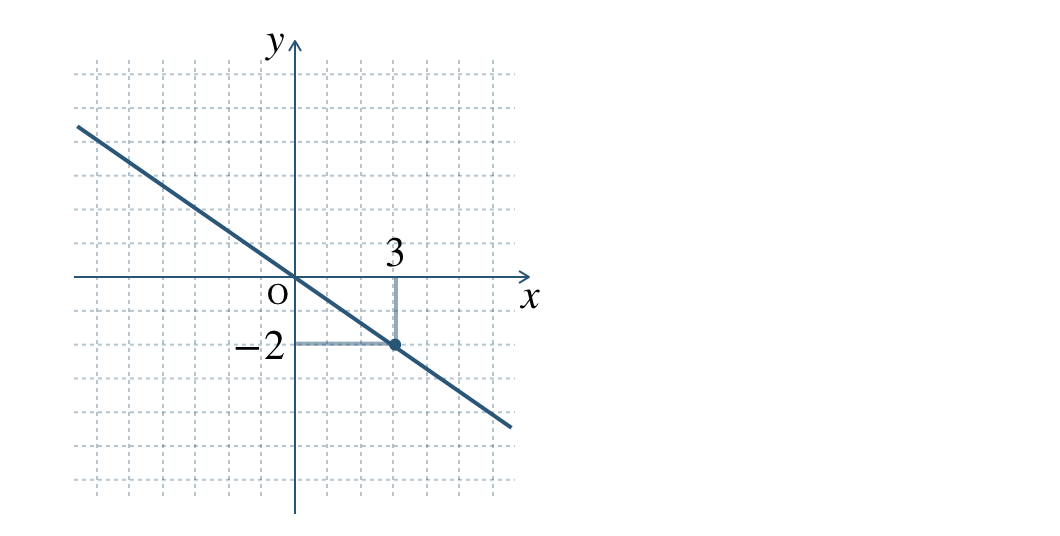
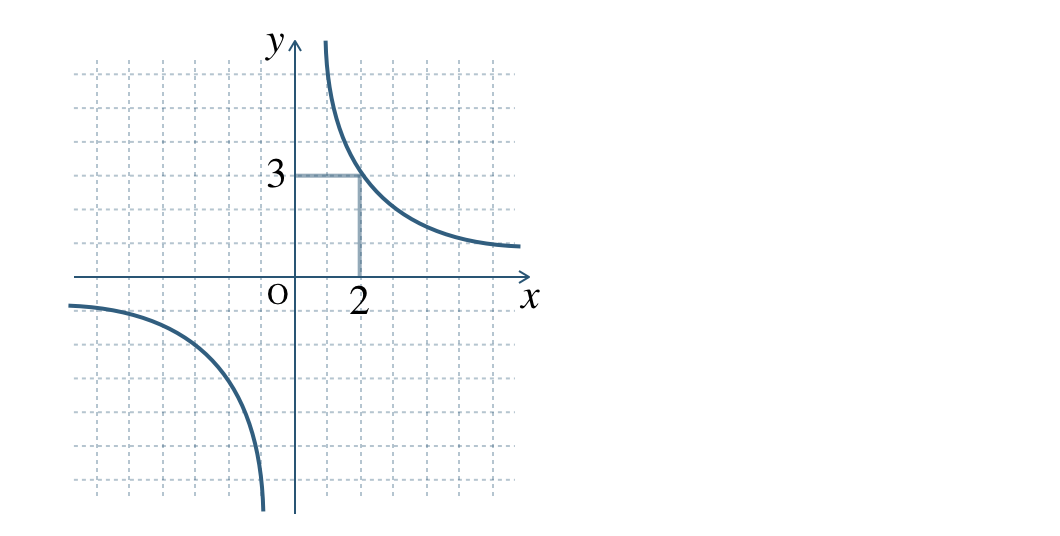
① \(\begin{split}y=\frac{\,4\,}{\,x\,}\end{split}\) ② \(\begin{split}y=-\frac{\,3\,}{\,x\,}\end{split}\)

比例の利用
AさんとBさんが \(800~{\rm m}\) を走った。スタートしてからの時間 \(x\) 分で走った道のり \(y~{\rm m}\) としたとき、AさんとBさんの \(x\) と \(y\) の関係をグラフで表すと下のようになった。
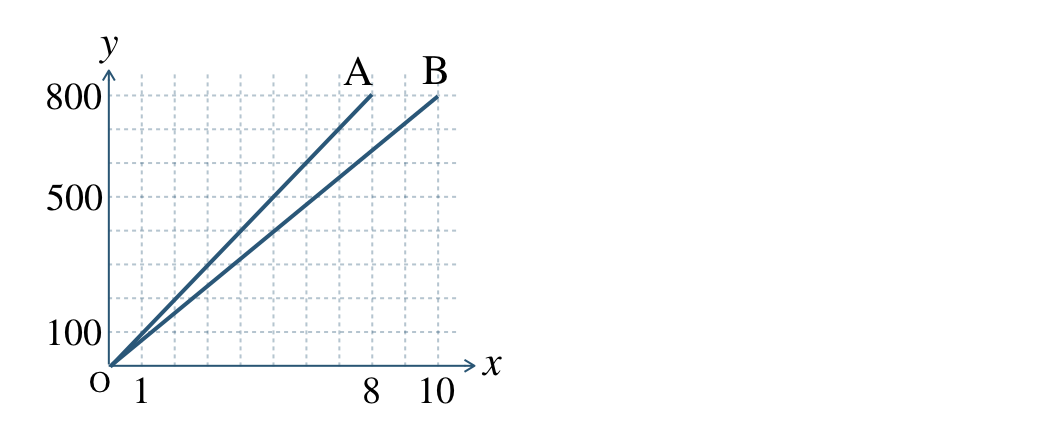
次の問いに答えよ。
\({\small (1)}~\)AさんとBさんはそれぞれ分速何 \({\rm m}\) で走ったか答えよ。
\({\small (2)}~\)AさんとBさんそれぞれの \(x\) と \(y\) の関係を式で表し、\(x\) の変域も答えよ。
\({\small (3)}~\)スタートして \(5\) 分後の2人の差は何 \({\rm m}\) か答えよ。
[ 解答を見る ]
【解答】
\({\small (1)}~\)
Aさん 分速 \(100~{\rm m}\)
Bさん 分速 \(80~{\rm m}\)
\({\small (2)}~\)
Aさん \(y=100x~~(0≦x≦8)\)
Bさん \(y=80x~~(0≦x≦10)\)
\({\small (3)}~\)
2人の差は \(100~{\rm m}\)

反比例の利用
電子レンジの出力と加熱時間は反比例することがわかっている。
\(500~{\rm W}\) で \(3\) 分温める必要がある食品について、次の問いに答えよ。
\({\small (1)}~\)電子レンジの出力を \(x~{\rm W}\)、時間を \(y\) 秒とするとき、\(x\) と \(y\) の関係を式で表せ。
\({\small (2)}~\)この食品を \(600~{\rm W}\) で温める場合、何分何秒に設定すればよいか答えよ。
\({\small (3)}~\)この食品を \(400~{\rm W}\) で温める場合、何分何秒に設定すればよいか答えよ。
[ 解答を見る ]
【解答】
\(\begin{split}{\small (1)}~y=\frac{\,90000\,}{\,x\,}\end{split}\)
\({\small (2)}~\)\(2\) 分 \(30\) 秒
\({\small (3)}~\)\(3\) 分 \(45\) 秒



