問題:図形の移動のまとめ
正方形 \({\rm ABCD}\) を次の図のようにア〜クの8つの合同な直角二等辺三角形に分けた。
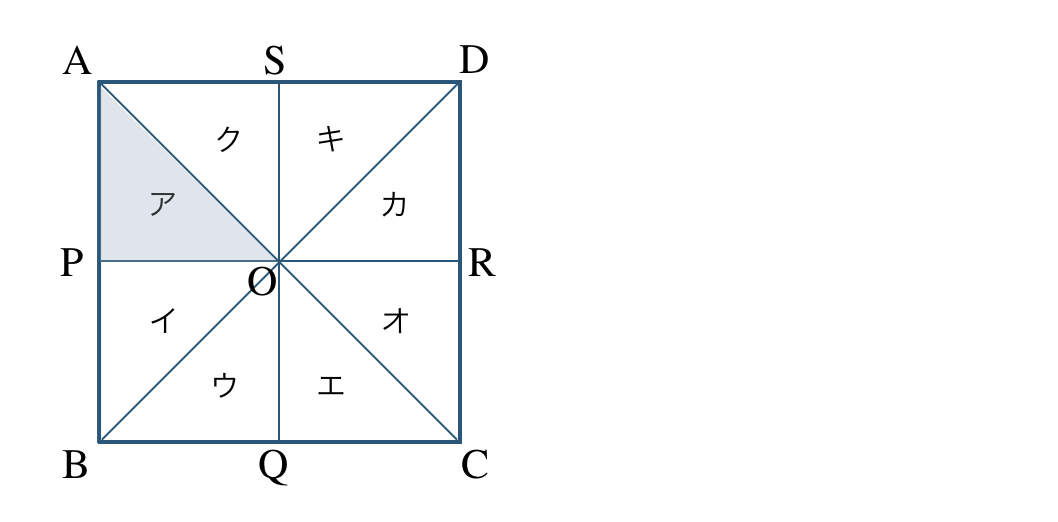
\({\small (1)}~\)次の条件の図形をア〜クから選べ。
① アを平行移動したときに重なる図形。
② アを平行移動したときに重なる図形。
\({\small (2)}~\)次の条件の図形をア〜クから選べ。
① アを線分 \({\rm PR}\) を対称の軸として、対称移動したときに重なる図形。
② アを線分 \({\rm SQ}\) を対称の軸として、対称移動したときに重なる図形。
③ アを線分 \({\rm AC}\) を対称の軸として、対称移動したときに重なる図形。
\({\small (3)}~\)次の条件の図形をア〜クから選べ。
① アを点 \({\rm O}\) を回転の中心として、時計回りに \(90^\circ\) 回転移動したときに重なる図形。
② アを点 \({\rm O}\) を回転の中心として、反時計回りに \(90^\circ\) 回転移動したときに重なる図形。
③ アを点 \({\rm O}\) を回転の中心として、点対称移動したときに重なる図形。
解法のPoint
正六角形 \({\rm ABCDEF}\) と対角線の交点 \({\rm O}\) において、次の図のようにア〜カの6つの合同な正三角形に分けた。

・アを平行移動すると ウ や オ に重なる。
・アを線分 \({\rm AO}\) を対称の軸として、
対称移動すると カ に重なる。
・アを線分 \({\rm CF}\) を対称の軸として、
対称移動すると エ に重なる。
・アを点 \({\rm O}\) を回転の中心として、
時計回りに \(60^\circ\) 回転移動すると カ に重なる。
・アを点 \({\rm O}\) を回転の中心として、
時計回りに \(120^\circ\) 回転移動すると オ に重なる。
・アを点 \({\rm O}\) を回転の中心として、
点対称移動すると エ に重なる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:図形の移動のまとめ
問題解説(1)
正方形 \({\rm ABCD}\) を次の図のようにア〜クの8つの合同な直角二等辺三角形に分けた。

\({\small (1)}~\)次の条件の図形をア〜クから選べ。
① アを平行移動したときに重なる図形。
② アを平行移動したときに重なる図形。
① アを平行移動すると、
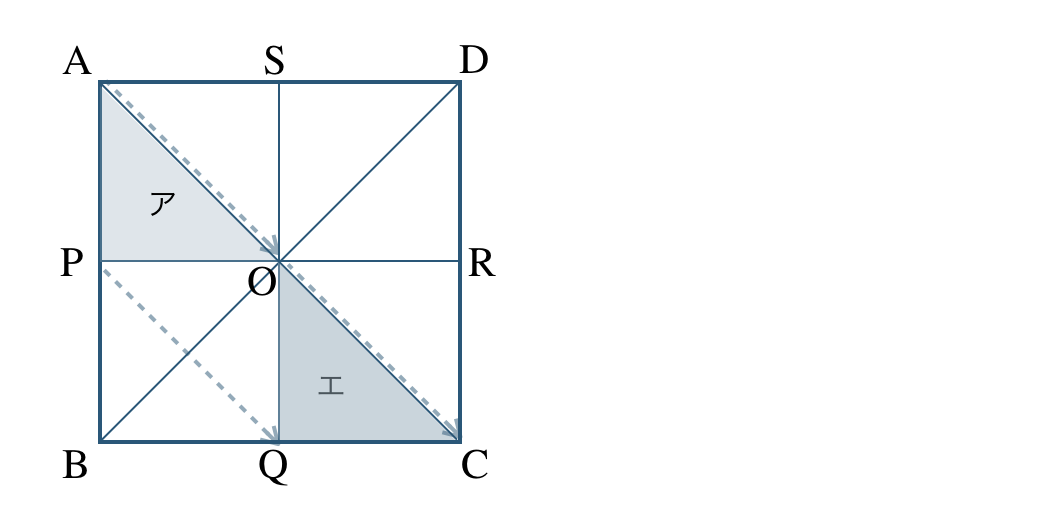
よって、エ と重なる
② イを平行移動すると、
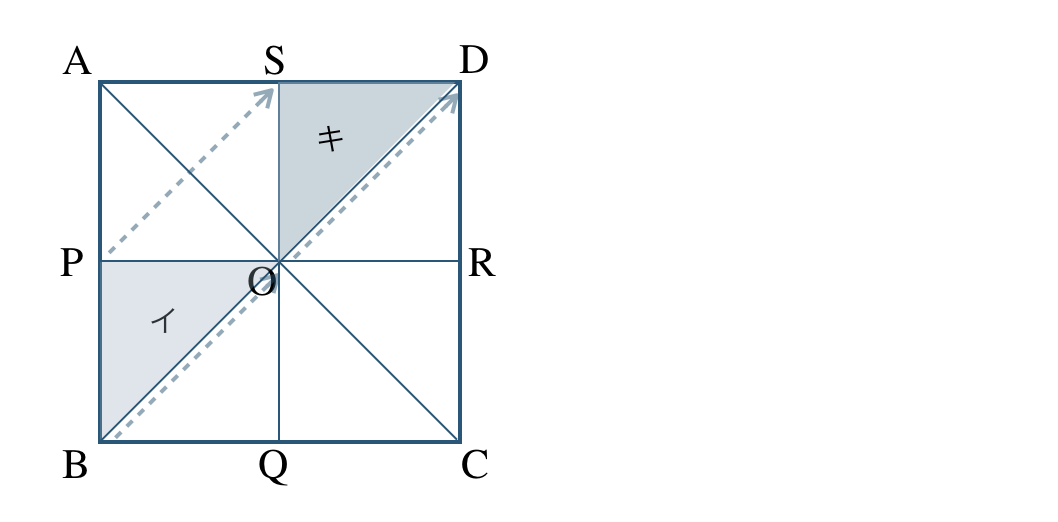
よって、キ と重なる
問題解説(2)
正方形 \({\rm ABCD}\) を次の図のようにア〜クの8つの合同な直角二等辺三角形に分けた。

\({\small (2)}~\)次の条件の図形をア〜クから選べ。
① アを線分 \({\rm PR}\) を対称の軸として、対称移動したときに重なる図形。
② アを線分 \({\rm SQ}\) を対称の軸として、対称移動したときに重なる図形。
③ アを線分 \({\rm AC}\) を対称の軸として、対称移動したときに重なる図形。
① 線分 \({\rm PR}\) を対称の軸として、対称移動すると、
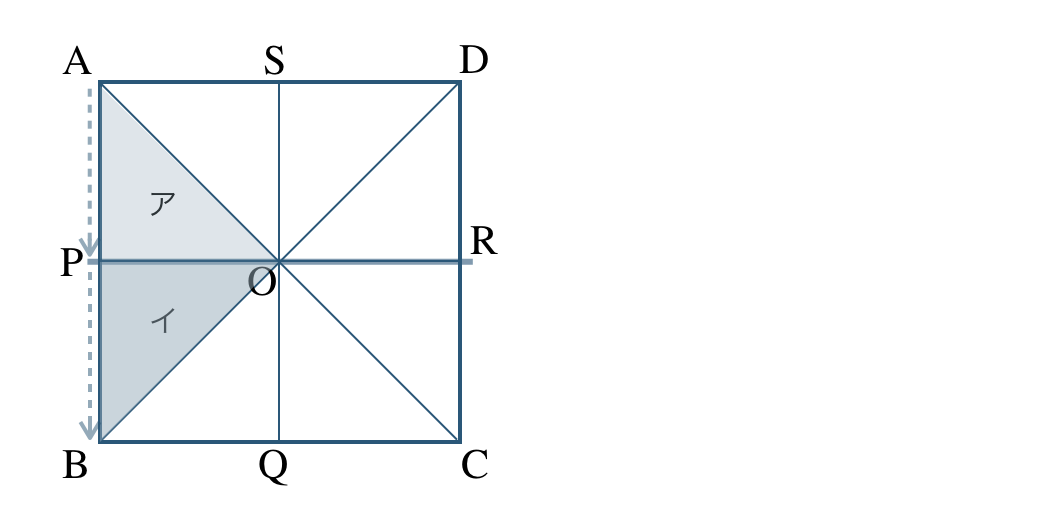
よって、イ と重なる
② 線分 \({\rm SQ}\) を対称の軸として、対称移動すると、
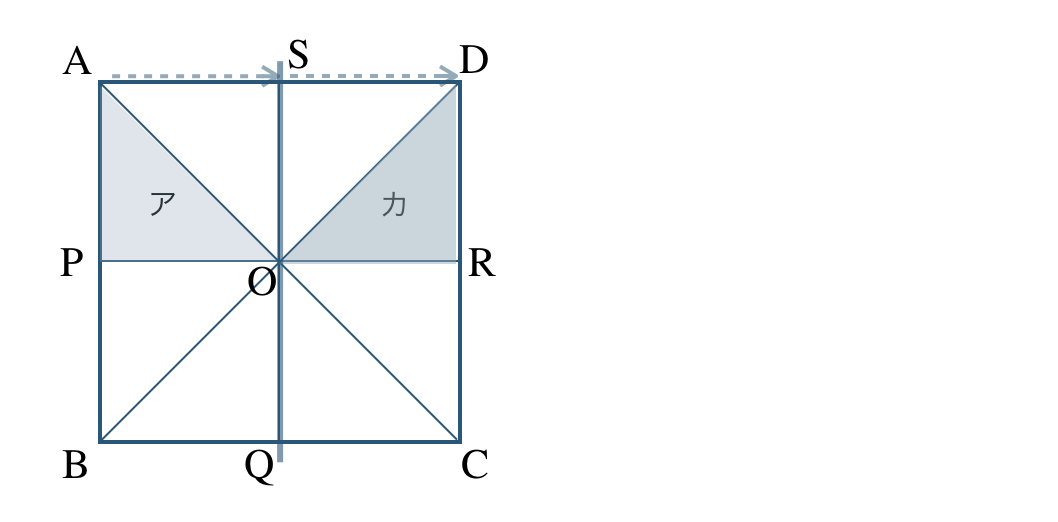
よって、カ と重なる
③ 線分 \({\rm AC}\) を対称の軸として、対称移動すると、
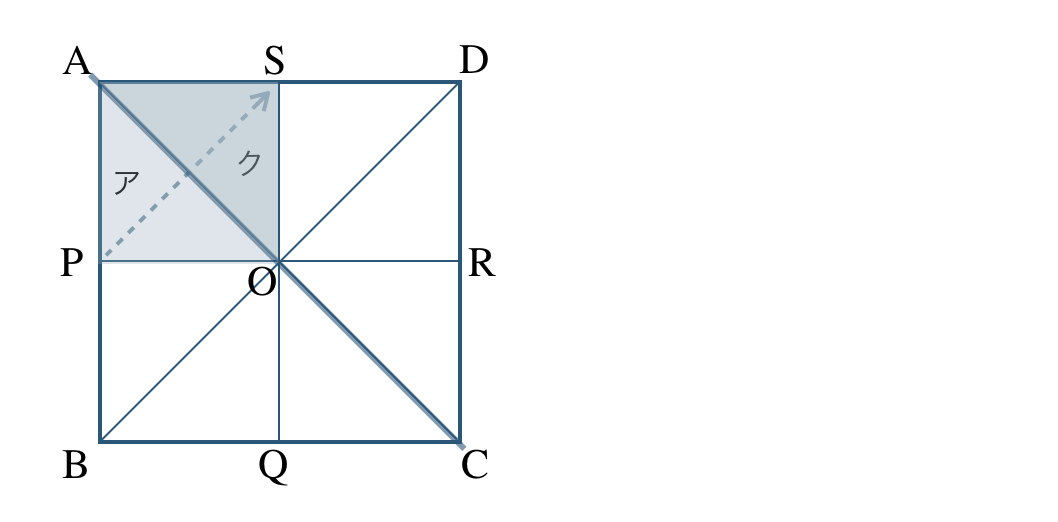
よって、ク と重なる
問題解説(3)
正方形 \({\rm ABCD}\) を次の図のようにア〜クの8つの合同な直角二等辺三角形に分けた。

\({\small (3)}~\)次の条件の図形をア〜クから選べ。
① アを点 \({\rm O}\) を回転の中心として、時計回りに \(90^\circ\) 回転移動したときに重なる図形。
② アを点 \({\rm O}\) を回転の中心として、反時計回りに \(90^\circ\) 回転移動したときに重なる図形。
③ アを点 \({\rm O}\) を回転の中心として、点対称移動したときに重なる図形。
① 点 \({\rm O}\) を回転の中心として、時計回りに \(90^\circ\) 回転移動すると、
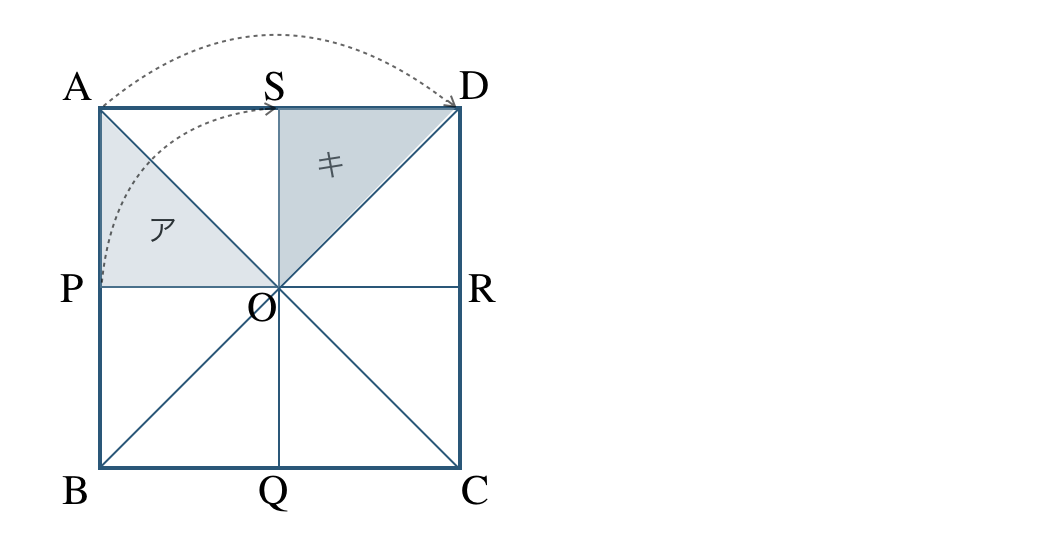
よって、キ と重なる
② 点 \({\rm O}\) を回転の中心として、反時計回りに \(90^\circ\) 回転移動すると、
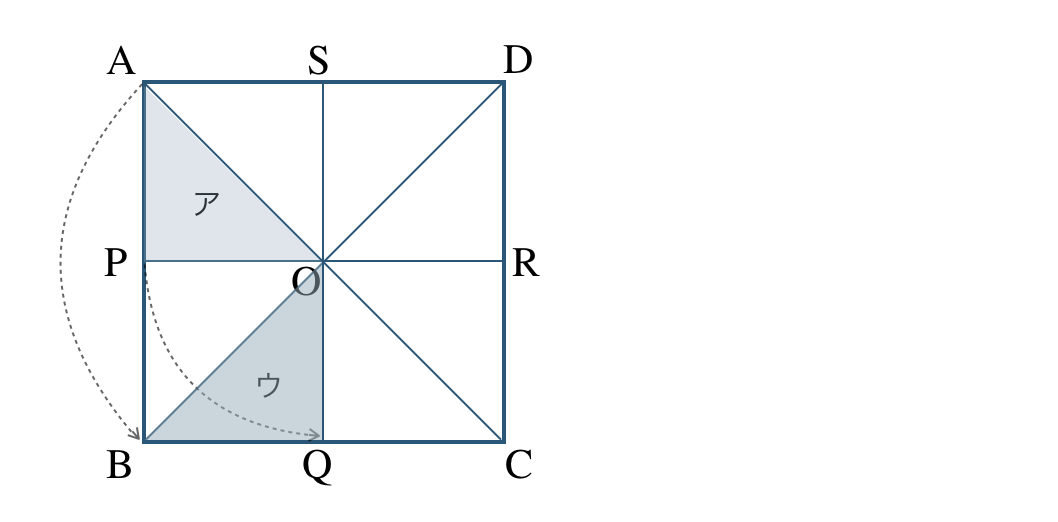
よって、ウ と重なる
③ 点 \({\rm O}\) を回転の中心として、点対称移動すると、
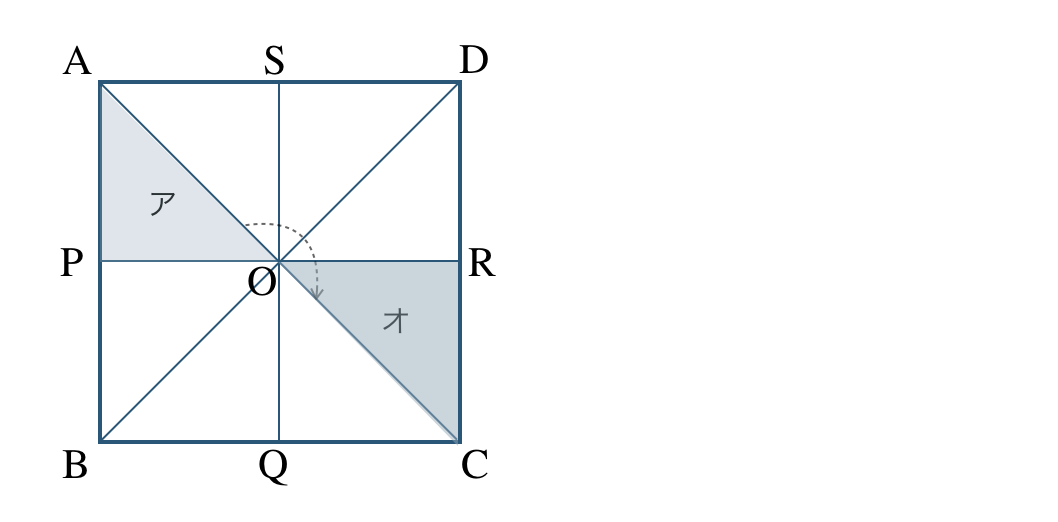
よって、オ と重なる



