今回の問題は「正多面体」です。
\(~\)数研出版 これからの数学１ p.191 問5~6
\(~\)東京書籍 新しい数学１ p.191~192 問5~7
\(~\)啓林館 未来へひろがる数学１ p.181 問1~2
問題
\({\small (1)}~\)次の①〜⑤の正多面体の名前を答えよ。また、面の形と１つの頂点に集まる面の数を答えよ。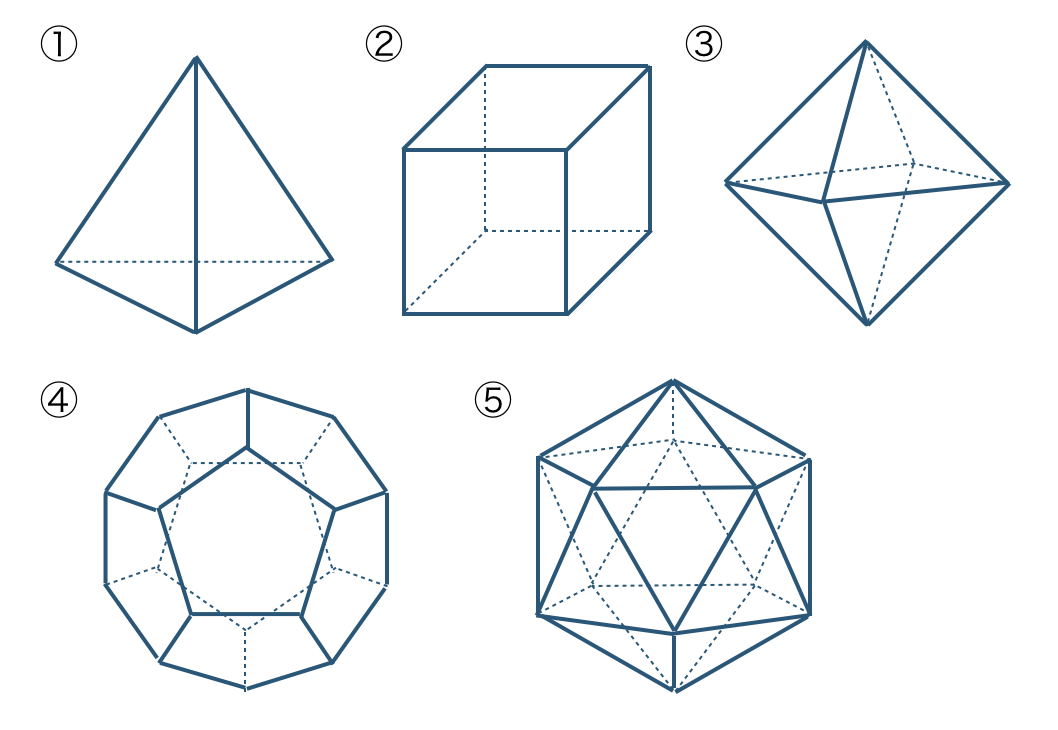
次の問いに答えよ。
\({\small (1)}~\)次の①〜⑤の正多面体の名前を答えよ。また、面の形と１つの頂点に集まる面の数を答えよ。
\({\small (2)}~\)次の立体はすべての面が正三角形の多面体であるが、正多面体ではない。この理由を答えよ。
Point：正多面体
へこみのない多面体のうち、
① すべての面が合同な正多角形である。
② どの頂点にも集まる面の数が等しい。
この２つの性質をもつ多面体を「正多面体」
正多面体の、面の形、※１つの頂点に集まる面の数、面の数、辺の数、頂点の数をまとめると、
正多面体
面の形
※
面
辺
頂点
正四面体
正三角形
\(3\)
\(4\)
\(6\)
\(4\)
正六面体
正方形
\(3\)
\(6\)
\(12\)
\(8\)
正八面体
正三角形
\(4\)
\(8\)
\(12\)
\(6\)
正十二面体
正五角形
\(3\)
\(12\)
\(30\)
\(20\)
正二十面体
正三角形
\(5\)
\(20\)
\(30\)
\(12\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
次のページ「解法のPointと問題解説」
