空間内の2直線の解法
空間内の2直線の位置関係は、
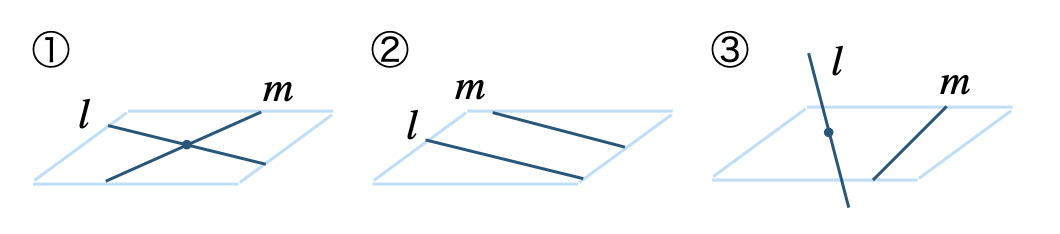
2直線が同じ平面上にあるとき、
① 2直線が交わる
② 2直線は平行である
2直線が同じ平面上になく、交わらないとき、
③ 2直線はねじれの位置にある
※ ねじれの位置は、交わる直線と平行な直線以外の直線となる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:空間内の2直線
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)次の長方形について、以下の辺を答えよ。
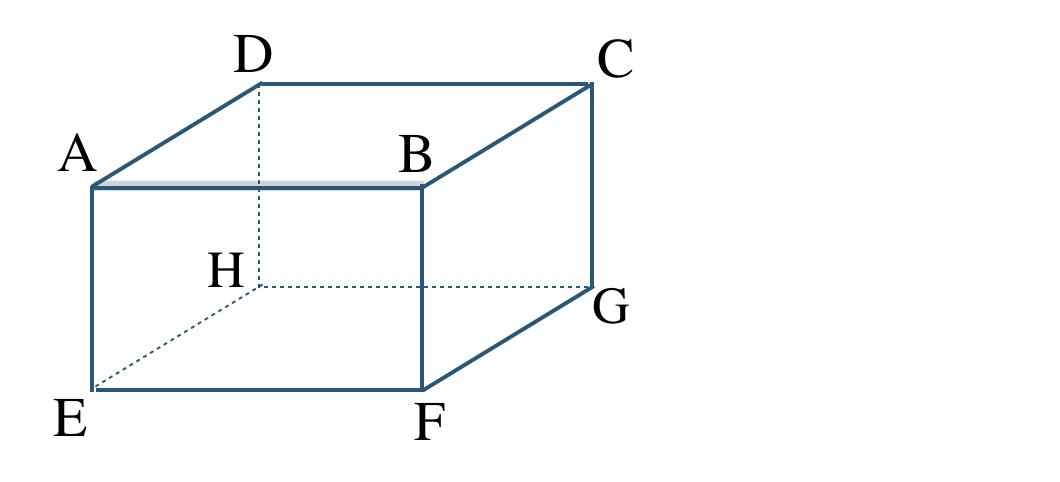
① 辺 \({\rm AB}\) と交わる辺。
② 辺 \({\rm AB}\) と平行な辺。
③ 辺 \({\rm AB}\) とねじれの位置にある辺。
① 辺 \({\rm AB}\) と同じ平面上の辺について、
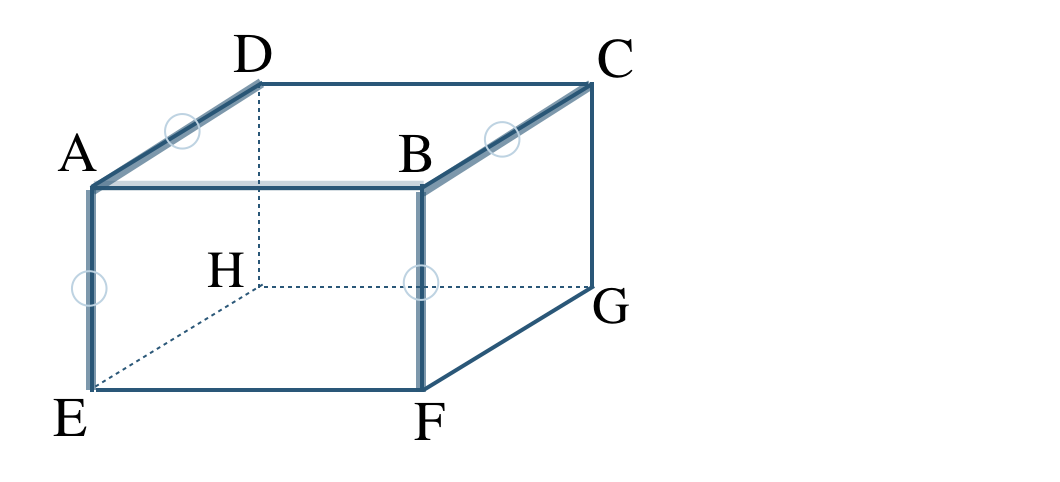
平面 \({\rm ABCD}\) で交わる辺は、辺 \({\rm AD~,~BC}\)
平面 \({\rm AEFB}\) で交わる辺は、辺 \({\rm AE~,~BF}\)
平面 \({\rm ABGH}\) で交わる辺はない
※ \({\rm AH~,~BG}\) は辺ではない。
よって、辺 \({\rm AD~,~BC~,~AE~,~BF}\) となる
② 辺 \({\rm AB}\) と同じ平面上の辺について、
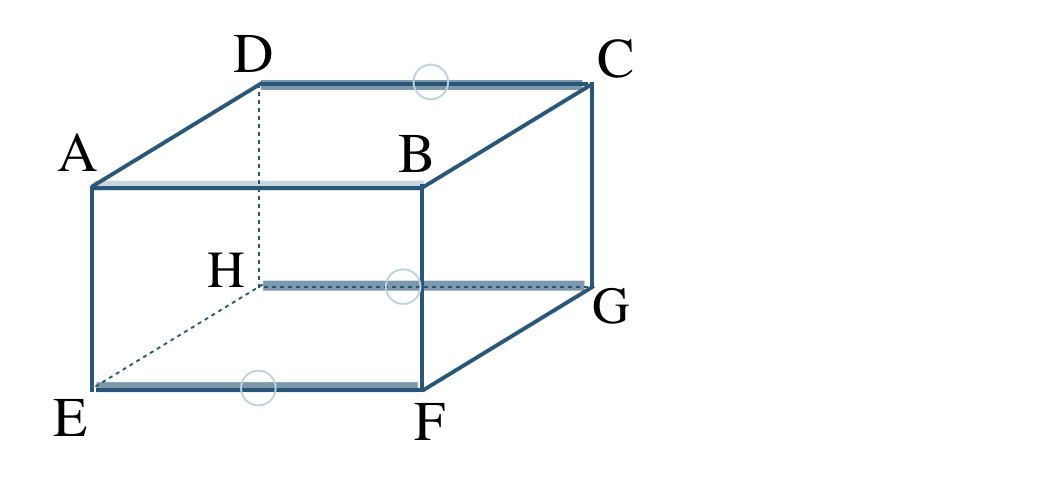
平面 \({\rm ABCD}\) で平行な辺は、辺 \({\rm DC}\)
平面 \({\rm AEFB}\) で平行な辺は、辺 \({\rm EF}\)
平面 \({\rm ABGH}\) で平行な辺は、辺 \({\rm HG}\)
よって、辺 \({\rm DC~,~EF~,~HG}\) となる
③ 辺 \({\rm AB}\) と交わらない辺で、同じ平面上にない辺は、
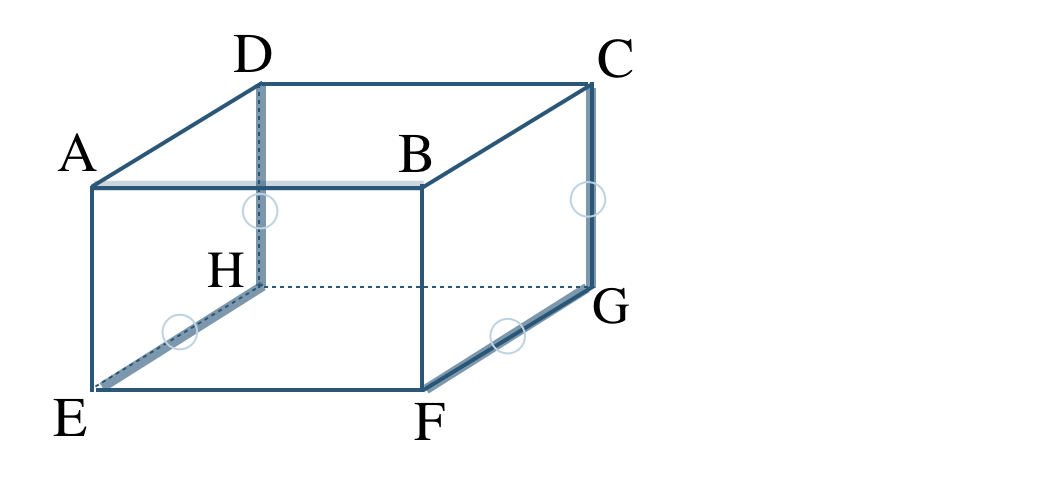
よって、ねじれの位置にある辺は、
辺 \({\rm EH~,~FG~,~DH~,~CG}\) となる
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)次の三角柱について、以下の直線を答えよ。

① 直線 \({\rm AB}\) と交わる直線。
② 直線 \({\rm AB}\) と平行な直線。
③ 直線 \({\rm AB}\) とねじれの位置にある直線。
① 直線 \({\rm AB}\) と同じ平面上の直線について、
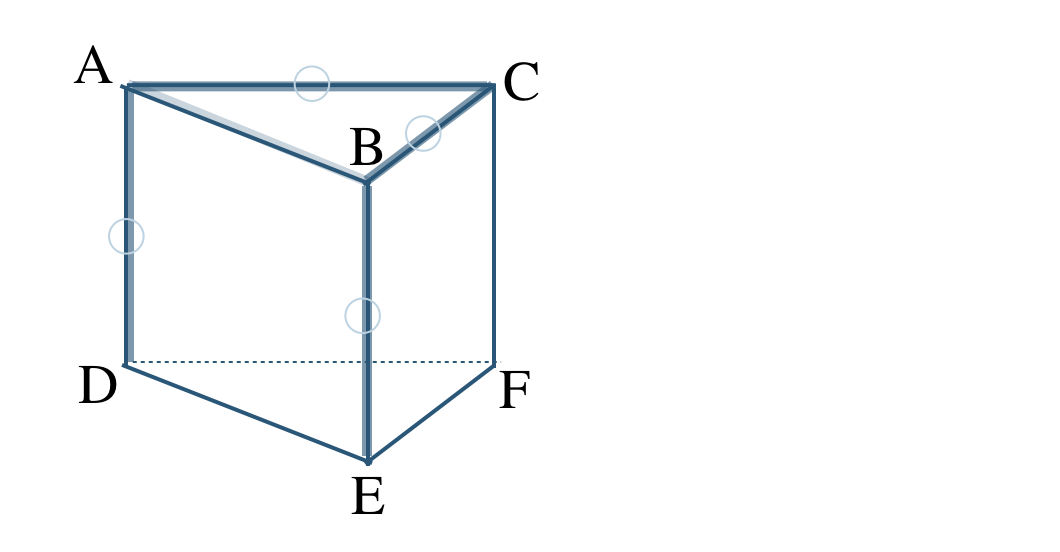
平面 \({\rm ABC}\) で交わる直線は、直線 \({\rm AC~,~BC}\)
平面 \({\rm ADEB}\) で交わる直線は、直線 \({\rm AD~,~BE}\)
よって、直線 \({\rm AC~,~BC~,~AD~,~BE}\) となる
② 直線 \({\rm AB}\) と同じ平面上の直線について、
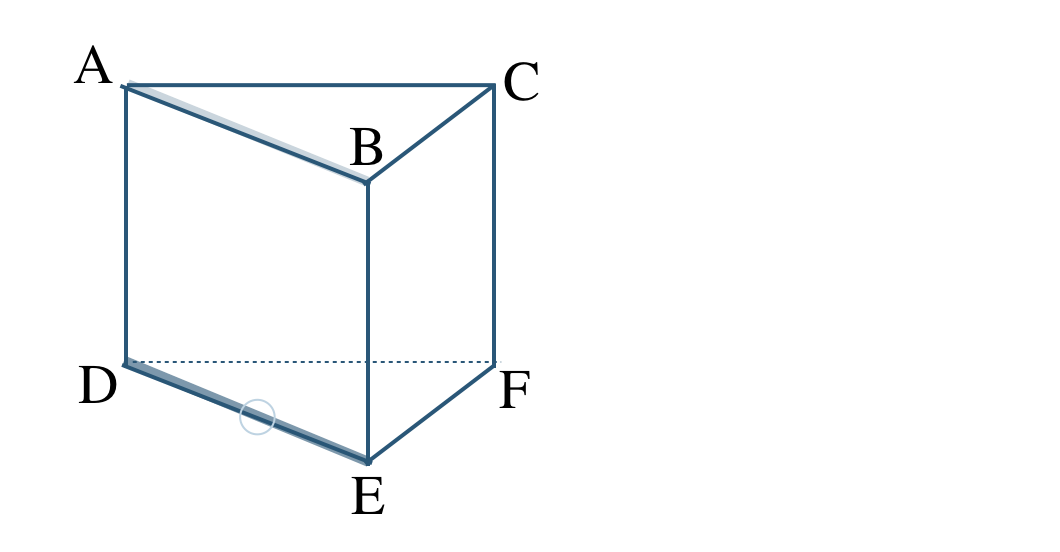
平面 \({\rm ABC}\) で平行な直線はない
平面 \({\rm ADEB}\) で平行な直線は、直線 \({\rm DE}\)
よって、直線 \({\rm DE}\) となる
③ 直線 \({\rm AB}\) と交わらない直線で、同じ平面上にない直線は、
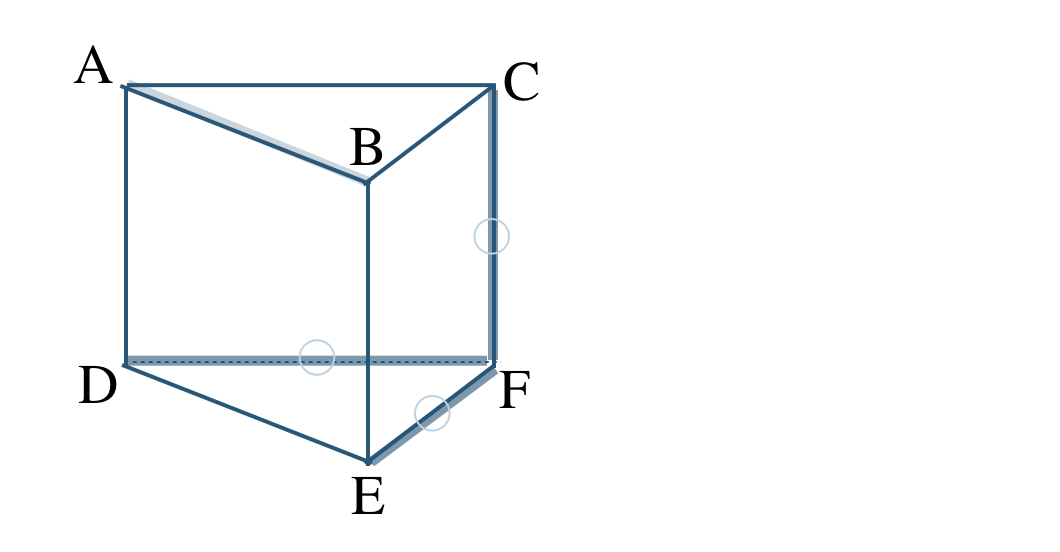
よって、ねじれの位置にある直線は、
直線 \({\rm CF~,~DF~,~EF}\) となる
問題解説(3)
次の問いに答えよ。
\({\small (3)}~\)次の正四面体について、以下の直線を答えよ。
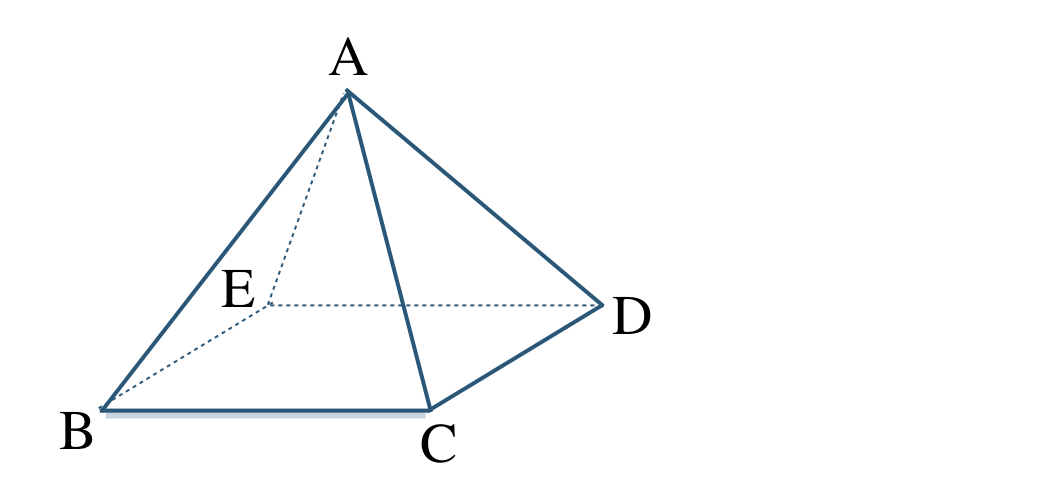
① 直線 \({\rm BC}\) と交わる直線。
② 直線 \({\rm BC}\) と平行な直線。
③ 直線 \({\rm BC}\) とねじれの位置にある直線。
① 直線 \({\rm BC}\) と同じ平面上の直線について、
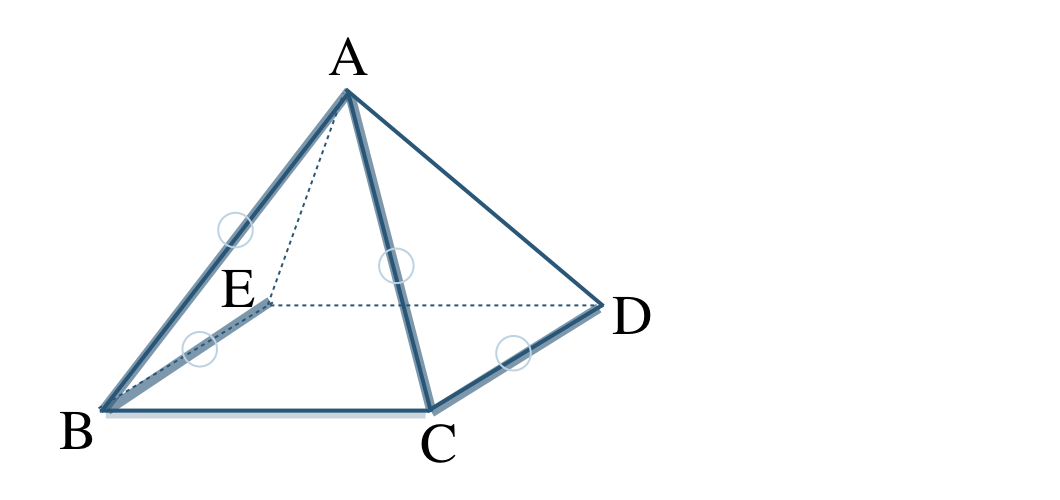
平面 \({\rm ABC}\) で交わる直線は、直線 \({\rm AB~,~AC}\)
平面 \({\rm BCDE}\) で交わる直線は、直線 \({\rm BE~,~CD}\)
よって、直線 \({\rm AB~,~AC~,~BE~,~CD}\) となる
② 直線 \({\rm BC}\) と同じ平面上の直線について、
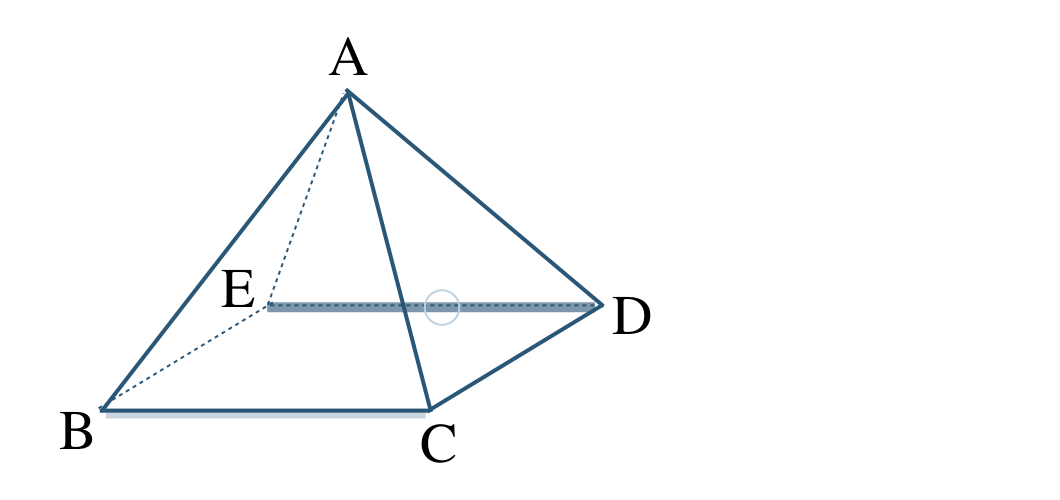
平面 \({\rm ABC}\) で平行な直線はない
平面 \({\rm BCDE}\) で平行な直線は、直線 \({\rm ED}\)
よって、直線 \({\rm ED}\) となる
③ 直線 \({\rm BC}\) と交わらない直線で、同じ平面上にない直線は、
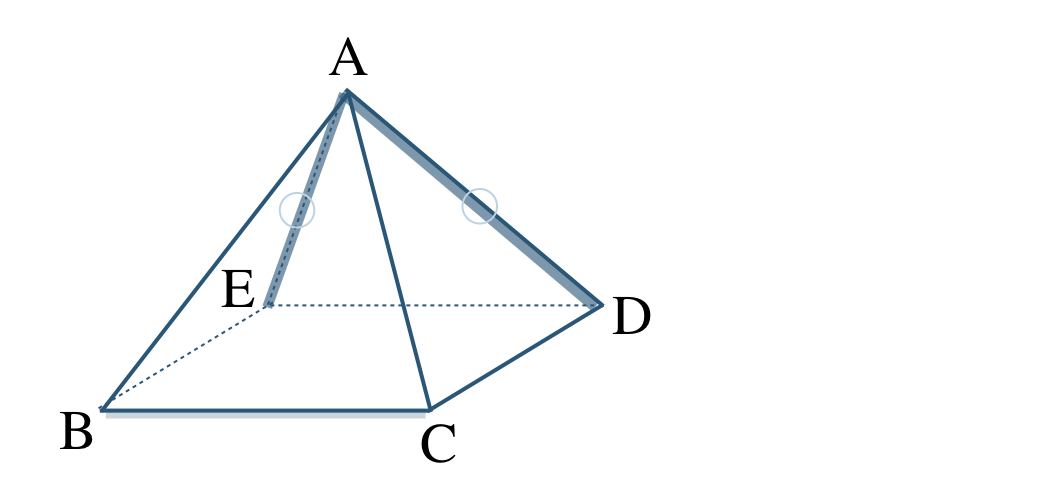
よって、ねじれの位置にある直線は、
直線 \({\rm AE~,~AD}\) となる



