データの代表値と範囲

データの代表値と範囲の解法

Point：データの代表値と範囲

データを小さき順に並べて、

　もっとも小さい値を「最小値」、
　もっとも大きい値を「最大値」、
　最大値 – 最小値の値を「範囲」という。
※ この範囲が大きいほど「データの散らばりが大きい」という。

データの中央にある値を「中央値」という。
\({\small (1)}~\)データの個数が奇数のとき

　真ん中の値が中央値となる。

\({\small (2)}~\)データの個数が偶数のとき

　真ん中２つの値の平均値が中央値となる。

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com

問題

次のデータは、Ａ市とＢ市の日ごとの最高気温を値の順に並べたものである。次の問いに答えよ。

\({\small (1)}~\)それぞれの市の最大値と最小値を求めよ。

Ａ市のデータより、もっとも大きい値ともっとも小さい値を読み取ると、

　Ａ市の最大値 \(31.4\) ℃、最小値 \(21.8\) ℃
Ｂ市のデータより、もっとも大きい値ともっとも小さい値を読み取ると、

　Ｂ市の最大値 \(33.5\) ℃、最小値 \(20.3\) ℃

したがって、答えは
　Ａ市の最大値 \(31.4\) ℃、最小値 \(21.8\) ℃
　Ｂ市の最大値 \(33.5\) ℃、最小値 \(20.3\) ℃
となる

問題

次のデータは、Ａ市とＢ市の日ごとの最高気温を値の順に並べたものである。次の問いに答えよ。

\({\small (2)}~\)それぞれの市の範囲を求めよ。また、どちらの市が散らばりが大きいか答えよ。

Ａ市の最大値 \(31.4\) ℃、最小値 \(21.8\) ℃であるので範囲は、

\(\begin{split}~~~31.4-21.8=9.6\end{split}\)

Ｂ市の最大値 \(33.5\) ℃、最小値 \(20.3\) ℃であるので範囲は、

\(\begin{split}~~~33.5-20.3=13.2\end{split}\)

また、Ｂ市の範囲の方が大きいので、散らばりが大きいのはＢ市となる

したがって、答えは
　Ａ市の範囲 \(9.6\)、Ｂ市の範囲 \(13.2\)
　散らばりが大きいのはＢ市
となる

問題

次のデータは、Ａ市とＢ市の日ごとの最高気温を値の順に並べたものである。次の問いに答えよ。

\({\small (3)}~\)それぞれの市の中央値を求めよ。

データは３０日分の偶数個であるので、中央値は小さい順に並べた１５番目と１６番目の平均値である
Ａ市の１５番目と１６番目は、

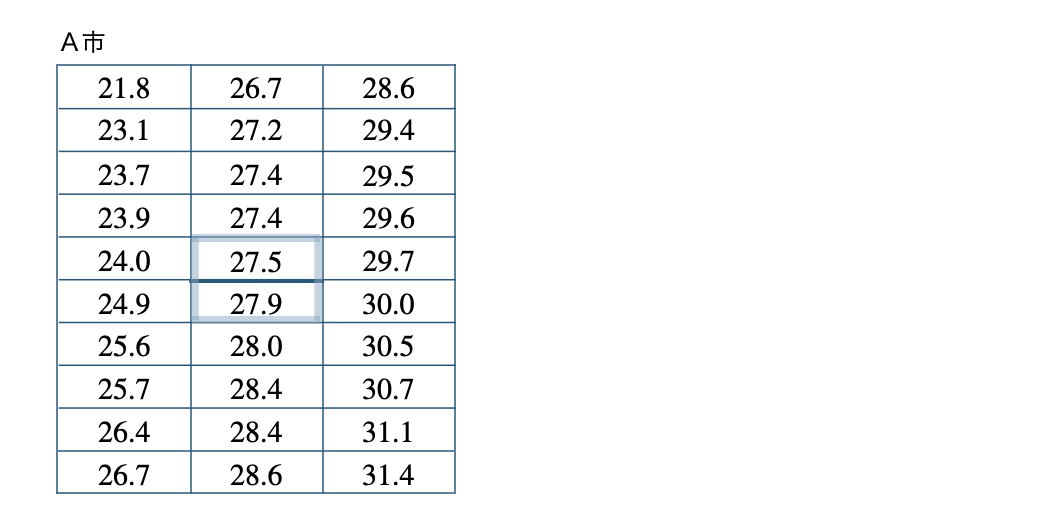
これより、

\(\begin{split}~~~\frac{\,27.5+27.9\,}{\,2\,}=\frac{\,55.4\,}{\,2\,}=27.7\end{split}\)

よって、中央値 \(27.7\) ℃
また、Ｂ市の１５番目と１６番目は、

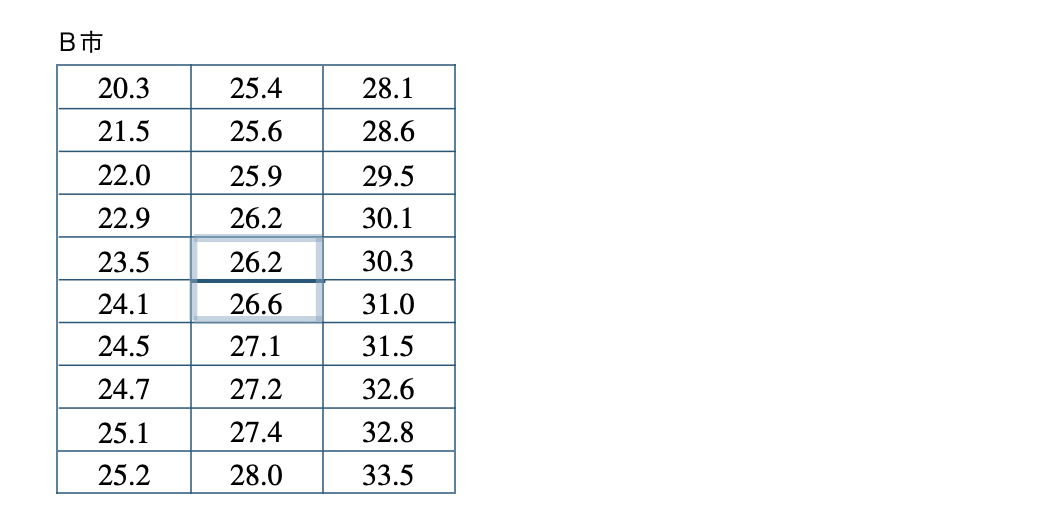
これより、

\(\begin{split}~~~\frac{\,26.2+26.6\,}{\,2\,}=\frac{\,52.8\,}{\,2\,}=26.4\end{split}\)

よって、中央値 \(26.4\) ℃

したがって、答えは
　Ａ市 \(27.7\) ℃、Ｂ市 \(26.4\) ℃
となる