今回の問題は「相対度数と累積相対度数」です。
\(~\)数研出版 これからの数学1 p.235~242 問1~2
\(~\)東京書籍 新しい数学1 p.227~229
\(~\)啓林館 未来へひろがる数学1 p.225~227 問6~9
問題
\({\small (2)}~\)以下の問いに答えよ。
① それぞれのグループの最頻値をとる階級の人数は全体の何%か求めよ。
② それぞれのグループの得点が \(10\) 点未満の割合を求めよ。
③ それぞれのグループの得点が \(6\) 点以上の割合がを求めよ。
\({\small (3)}~\)それぞれのグループの相対度数のヒストグラムと度数折れ線をかけ。
\({\small (4)}~\)それぞれのグループの累積相対度数のヒストグラムと度数折れ線をかけ。
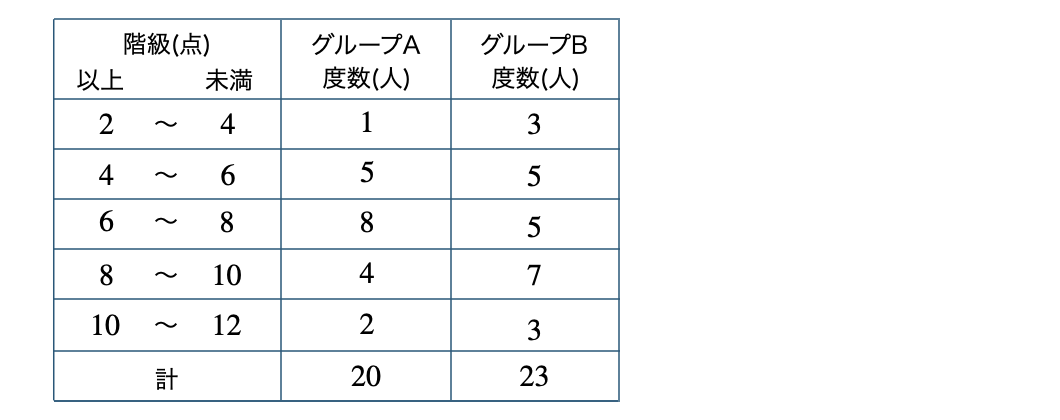
次の表は、\(20\) 人のグループAと \(23\) 人のグループBのあるゲームの得点の度数分布表である。次の問いに答えよ。

\({\small (1)}~\)それぞれのグループの相対度数、累積度数、累積相対度数の表を完成させよ。
\({\small (2)}~\)以下の問いに答えよ。
① それぞれのグループの最頻値をとる階級の人数は全体の何%か求めよ。
② それぞれのグループの得点が \(10\) 点未満の割合を求めよ。
③ それぞれのグループの得点が \(6\) 点以上の割合がを求めよ。
\({\small (3)}~\)それぞれのグループの相対度数のヒストグラムと度数折れ線をかけ。
\({\small (4)}~\)それぞれのグループの累積相対度数のヒストグラムと度数折れ線をかけ。
Point:相対度数
このとき、小数第2位までを求めて、割り切れないときは、小数第3位を四捨五入する。
Bの \(9\) 以上 \(12\) 未満の階級での相対度数は、
\(4{\, \small \div \,}22=0.181\cdots=0.18\)
度数の合計が違うデータを比較するとき、全体に対する割合で比較する。
この割合を「相対度数」といい、
相対度数は、
(その階級の度数) ÷ (度数の合計) で求める。
このとき、小数第2位までを求めて、割り切れないときは、小数第3位を四捨五入する。

Aの \(9\) 以上 \(12\) 未満の階級での相対度数は、
\(9{\, \small \div \,}23=0.391\cdots=0.39\)
Bの \(9\) 以上 \(12\) 未満の階級での相対度数は、
\(4{\, \small \div \,}22=0.181\cdots=0.18\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
Point:累積度数と累積相対度数

最初の階級からある階級までの度数の合計を「累積度数」といい、相対度数の合計を「累積相対度数」という。
また、累積相対度数は、
(その階級の累積度数) ÷ (度数の合計)
でも求めことができる。

相対度数は割合を表すので、
たとえば、\(12\) 未満の割合を求めるとき、
\(12\) 未満の累計相対度数の \(0.70\) が割合となる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
次のページ「解法のPointと問題解説」


