1次関数のグラフと傾きの解法
Point:1次関数のグラフと傾き
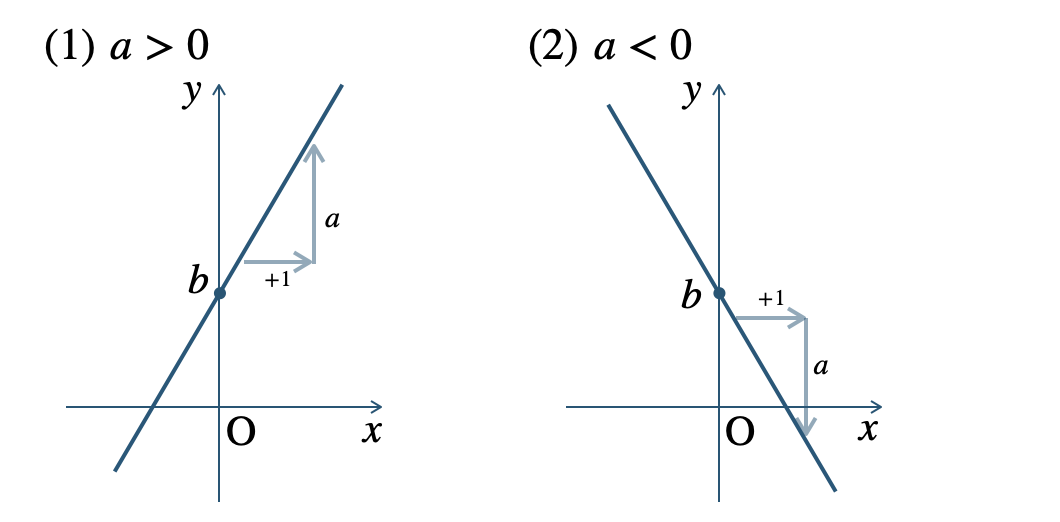
\(a\) =(変化の割合)=(傾き)
\({\small (1)}~\)\(a>0\) のとき、直線は右上がりとなる。
※ \(a\) の値が大きくなると、直線の傾きぐあいも大きくなる。
\({\small (2)}~\)\(a<0\) のとき、直線は右下がりとなる。
例えば、直線 \(y=2x+1\) の傾きは \(2\) で、
右に \(1\) 進むときは、上に \(2{\, \small \times \,}1=2\) 進む
右に \(2\) 進むときは、上に \(2{\, \small \times \,}2=4\) 進む
右に \(3\) 進むときは、上に \(2{\, \small \times \,}3=6\) 進む
1次関数 \(y=ax+b\) のグラフは直線となり、\(a\) の値をこの直線の「傾き」という。
\(a\) =(変化の割合)=(傾き)
\({\small (1)}~\)\(a>0\) のとき、直線は右上がりとなる。
※ \(a\) の値が大きくなると、直線の傾きぐあいも大きくなる。
\({\small (2)}~\)\(a<0\) のとき、直線は右下がりとなる。

■ 直線の進み方
例えば、直線 \(y=2x+1\) の傾きは \(2\) で、
右に \(1\) 進むときは、上に \(2{\, \small \times \,}1=2\) 進む
右に \(2\) 進むときは、上に \(2{\, \small \times \,}2=4\) 進む
右に \(3\) 進むときは、上に \(2{\, \small \times \,}3=6\) 進む
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:1次関数のグラフと傾き
問題解説(1)
問題
\({\small (1)}~\)次の直線において、右に \(1\) 進むとき、右に \(3\) 進むときはそれぞれ上に(または下に)どれだけ進むか答えよ。
① \(\begin{split}y=x+3\end{split}\)
② \(\begin{split}y=-2x+1\end{split}\)
③ \(\begin{split}y=3x-5\end{split}\)
次の問いに答えよ。
\({\small (1)}~\)次の直線において、右に \(1\) 進むとき、右に \(3\) 進むときはそれぞれ上に(または下に)どれだけ進むか答えよ。
① \(\begin{split}y=x+3\end{split}\)
② \(\begin{split}y=-2x+1\end{split}\)
③ \(\begin{split}y=3x-5\end{split}\)
① \(\begin{split}y=x+3\end{split}\)
変化の割合が \(1\) であるので、
※ \(x=1{\, \small \times \,} x\) より、\(x\) の係数は \(1\)。
右に \(1\) 進むとき、\(1{\, \small \times \,}1=1\)
これより、上に \(1\) 進む
右に \(3\) 進むとき、\(1{\, \small \times \,}3=3\)
これより、上に \(3\) 進む
② \(\begin{split}y=-2x+1\end{split}\)
変化の割合が \(-2\) であるので、
右に \(1\) 進むとき、\(-2{\, \small \times \,}1=-2\)
これより、下に \(2\) 進む
右に \(3\) 進むとき、\(-2{\, \small \times \,}3=-6\)
これより、下に \(6\) 進む
③ \(\begin{split}y=3x-5\end{split}\)
変化の割合が \(3\) であるので、
右に \(1\) 進むとき、\(3{\, \small \times \,}1=3\)
これより、上に \(3\) 進む
右に \(3\) 進むとき、\(3{\, \small \times \,}3=9\)
これより、上に \(9\) 進む
問題解説(2)
問題
\({\small (2)}~\)次の直線の傾きを答えよ。また、右上がりか右下がりか答えよ。
\({\small (2)}~\)次の直線の傾きを答えよ。また、右上がりか右下がりか答えよ。
① \(\begin{split}y=-5x+1\end{split}\)
② \(\begin{split}y=\frac{\,3\,}{\,4\,}x+\frac{\,1\,}{\,2\,}\end{split}\)
③ \(\begin{split}y=-x\end{split}\)
次の問いに答えよ。
\({\small (2)}~\)次の直線の傾きを答えよ。また、右上がりか右下がりか答えよ。
\({\small (2)}~\)次の直線の傾きを答えよ。また、右上がりか右下がりか答えよ。
① \(\begin{split}y=-5x+1\end{split}\)
② \(\begin{split}y=\frac{\,3\,}{\,4\,}x+\frac{\,1\,}{\,2\,}\end{split}\)
③ \(\begin{split}y=-x\end{split}\)
① \(\begin{split}y=-5x+1\end{split}\)
\(x\) の係数 \(-5\) より、傾き \(-5\) となる
また、傾きが負の数であるので、
直線は右下がりのグラフとなる
② \(\begin{split}y=\frac{\,3\,}{\,4\,}x+\frac{\,1\,}{\,2\,}\end{split}\)
\(x\) の係数 \(\begin{split}{\frac{\,3\,}{\,4\,}}\end{split}\) より、傾き \(\begin{split}{\frac{\,3\,}{\,4\,}}\end{split}\) となる
また、傾きが正の数であるので、
直線は右上がりのグラフとなる
③ \(\begin{split}y=-x\end{split}\)
\(x\) の係数 \(-1\) より、傾き \(-1\) となる
※ \(-x=-1{\, \small \times \,} x\) より、\(x\) の係数は \(-1\)。
また、傾きが負の数であるので、
直線は右下がりのグラフとなる

【問題一覧】中2|1次関数
このページは「中学数学2 1次関数」の問題一覧ページとなります。解説の見たい単元名がわからないときは...


