直角三角形の合同条件の解法
2つの直角三角形は次のどれかが成り立つとき、
合同 \(\triangle {\rm ABC}\equiv \triangle {\rm A’B’C’}\) である。
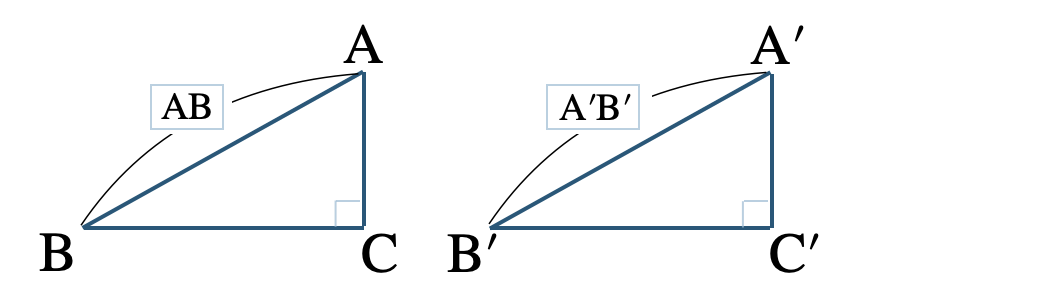
\(\angle{\rm C}=\angle{\rm C’}=90^\circ\) の直角三角形の、
① 斜辺と1つの鋭角がそれぞれ等しい。
\({\rm AB=A’B’}\) と、
\({\rm \angle A=\angle A’}\) または、\({\rm \angle B=\angle B’}\)
② 斜辺と他の1辺がそれぞれ等しい。
\({\rm AB=A’B’}\) と、
\({\rm AC=A’C’}\) または、\({\rm BC=B’C’}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:直角三角形の合同条件
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)次の図において、合同な図形を見つけ記号 \(\equiv\) で表し、合同条件を答えよ。
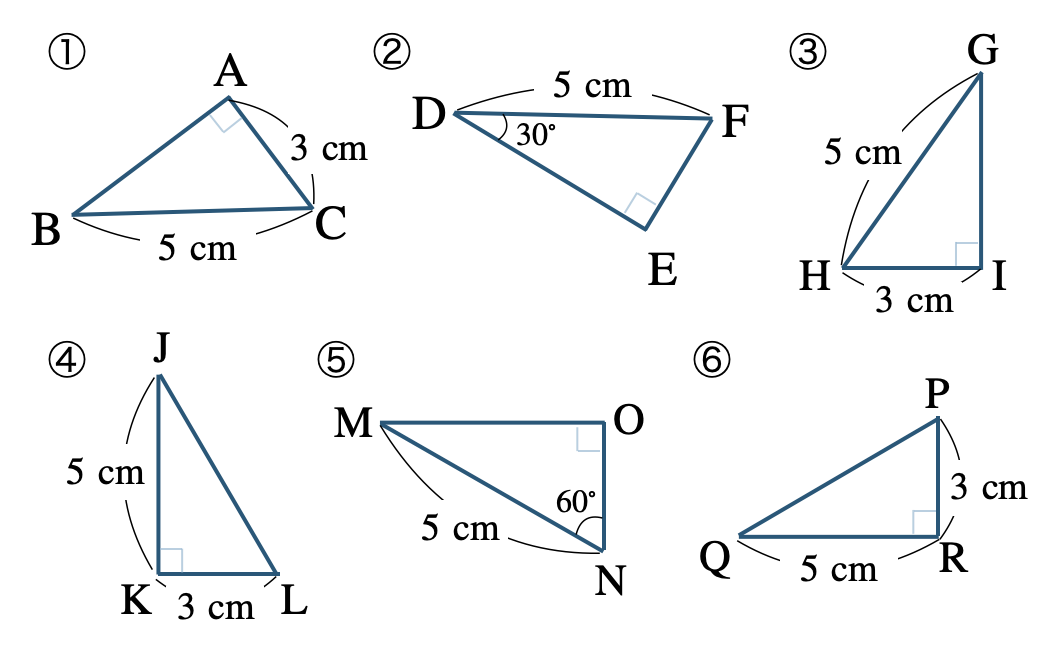
①と③の向きをそろえると、
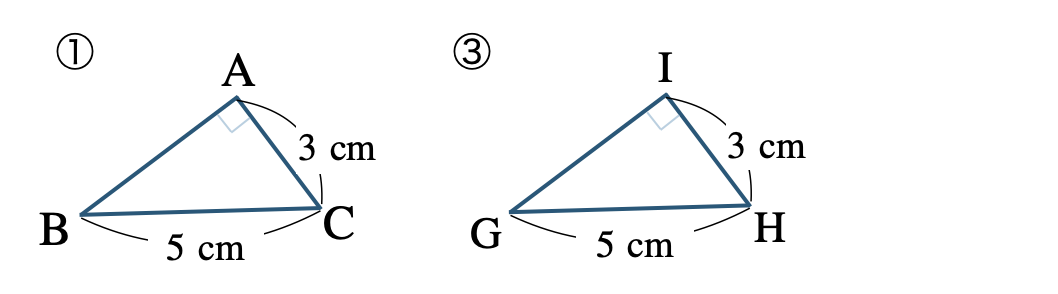
\(\angle{\rm A}=\angle{\rm I}=90^\circ\) (直角)
\({\rm BC=GH}=5~{\rm cm}\) (斜辺)
\({\rm AC=IH}=3~{\rm cm}\)
対応する頂点は、
\({\rm A}\) と \({\rm I}\)、\({\rm B}\) と \({\rm G}\)、\({\rm C}\) と \({\rm H}\)
であるので、
\(\triangle {\rm ABC}\equiv\triangle {\rm IGH}\)
合同条件は、
直角三角形の斜辺と他の1辺がそれぞれ等しい
となる
②と⑤の向きをそろえると、
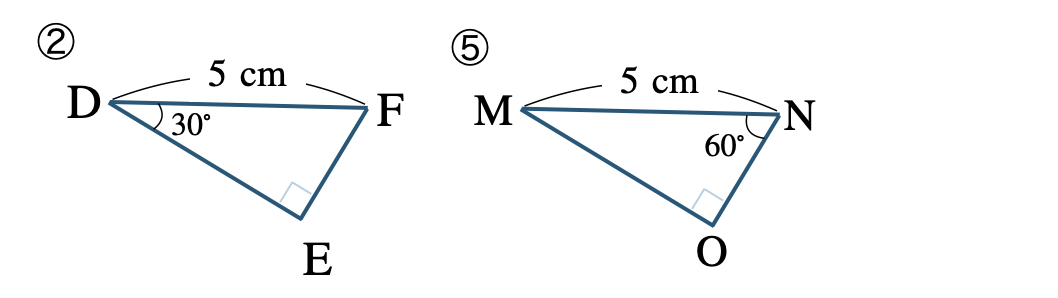
\(\angle{\rm M}=90^\circ-60^\circ=30^\circ\) より、
\(\angle{\rm E}=\angle{\rm O}=90^\circ\) (直角)
\({\rm DF=MN}=5~{\rm cm}\) (斜辺)
\(\angle{\rm D}=\angle{\rm M}=30^\circ\)
対応する頂点は、
\({\rm D}\) と \({\rm M}\)、\({\rm E}\) と \({\rm O}\)、\({\rm F}\) と \({\rm N}\)
であるので、
\(\triangle {\rm DEF}\equiv\triangle {\rm MON}\)
合同条件は、
直角三角形の斜辺と1つの鋭角がそれぞれ等しい
となる
④と⑥の向きをそろえると、
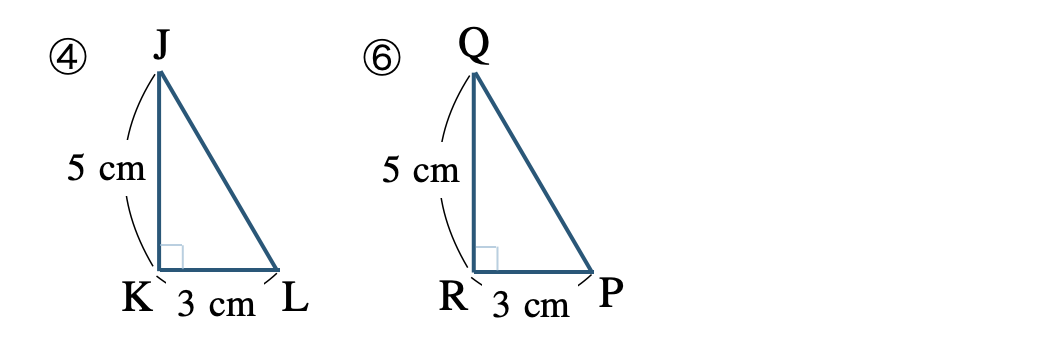
\(\angle{\rm K}=\angle{\rm R}=90^\circ\) (直角)
\({\rm JK=QR}=5~{\rm cm}\)
\({\rm KL=RP}=3~{\rm cm}\)
対応する頂点は、
\({\rm J}\) と \({\rm Q}\)、\({\rm K}\) と \({\rm R}\)、\({\rm L}\) と \({\rm P}\)
であるので、
\(\triangle {\rm JKL}\equiv\triangle {\rm QRP}\)
合同条件は、
2組の辺とその間の角がそれぞれ等しい
となる
(※ 斜辺が等しいことがわかっていないので、三角形の合同条件を使う。)
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)次の図において、合同な図形を見つけ記号 \(\equiv\) で表し、合同条件を答えよ。
① \(\triangle {\rm ABC}\) は \({\rm AB=AC}\) の二等辺三角形で、点 \({\rm A}\) から辺 \({\rm BC}\) におろした垂線との交点を \({\rm D}\) とする。
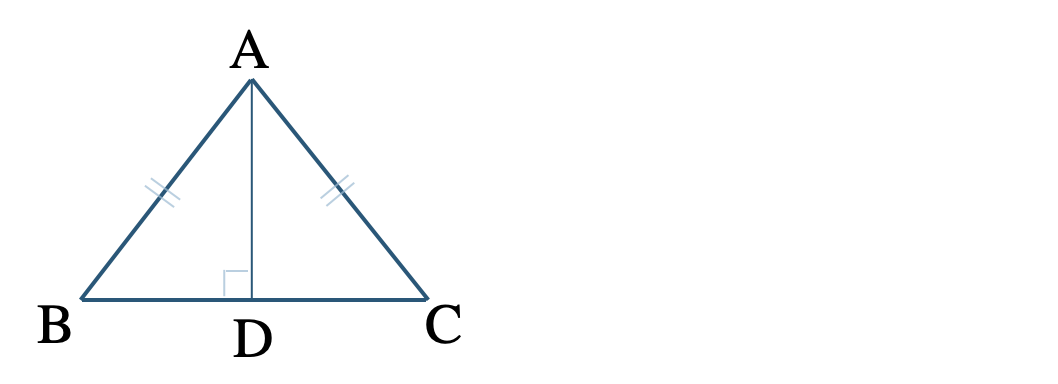
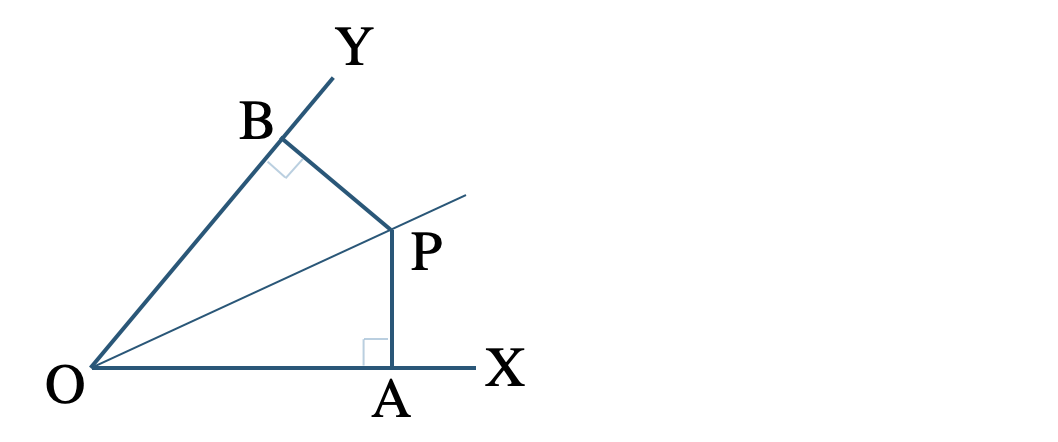
② 直線 \({\rm OP}\) は \(\angle{\rm XOY}\) の二等分線で、点 \({\rm P}\) からそれぞれ直線 \({\rm OX~,~OY}\) におろした垂線との交点を \({\rm A~,~B}\) とする。
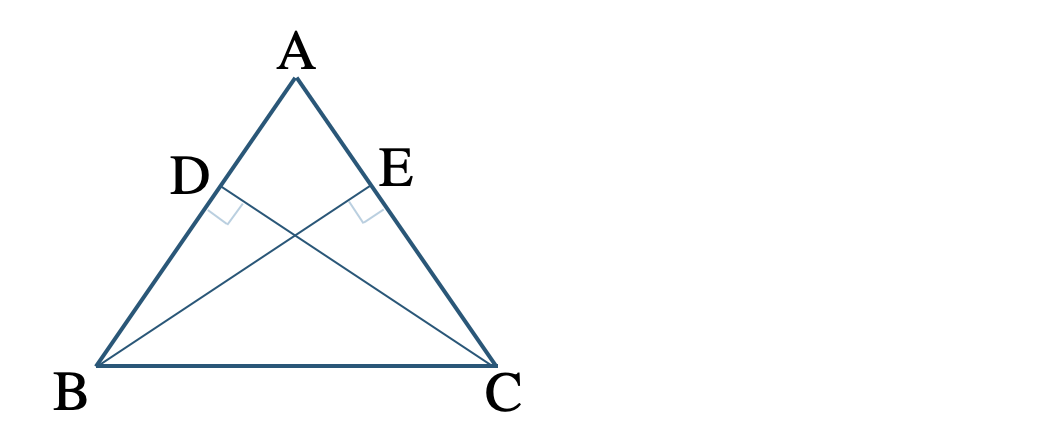
③ \(\triangle {\rm ABC}\) は \({\rm AB=AC}\) の二等辺三角形で、点 \({\rm B~,~C}\) からそれぞれ辺 \({\rm AC~,~AB}\) におろした垂線との交点を \({\rm E~,~D}\) とする。
① \(\triangle {\rm ABD}\) と \(\triangle {\rm ACD}\) の向きをそろえると、
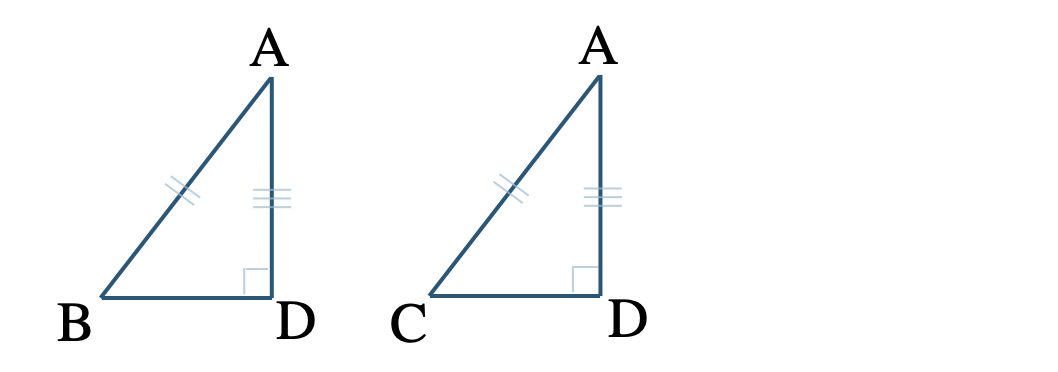
\(\angle{\rm ADB}=\angle{\rm ADC}=90^\circ\) (直角)
二等辺三角形より、
\({\rm AB=AC}\) (斜辺)
\({\rm AD=AD}\)
よって、
\(\triangle {\rm ABD}\equiv\triangle {\rm ACD}\)
合同条件は、
直角三角形の斜辺と他の1辺がそれぞれ等しい
となる
② \(\triangle {\rm POA}\) と \(\triangle {\rm POB}\) の向きをそろえると、
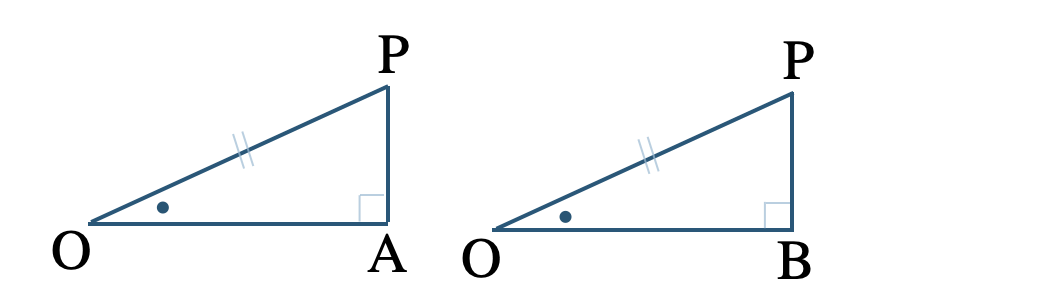
\(\angle{\rm PAO}=\angle{\rm PBO}=90^\circ\) (直角)
\({\rm OP=OP}\) (斜辺)
角の二等分線より、
\(\angle{\rm POA}=\angle{\rm POB}\)
よって、
\(\triangle {\rm POA}\equiv\triangle {\rm POB}\)
合同条件は、
直角三角形の斜辺と1つの鋭角がそれぞれ等しい
となる
③ \(\triangle {\rm DBC}\) と \(\triangle {\rm ECB}\) の向きをそろえると、
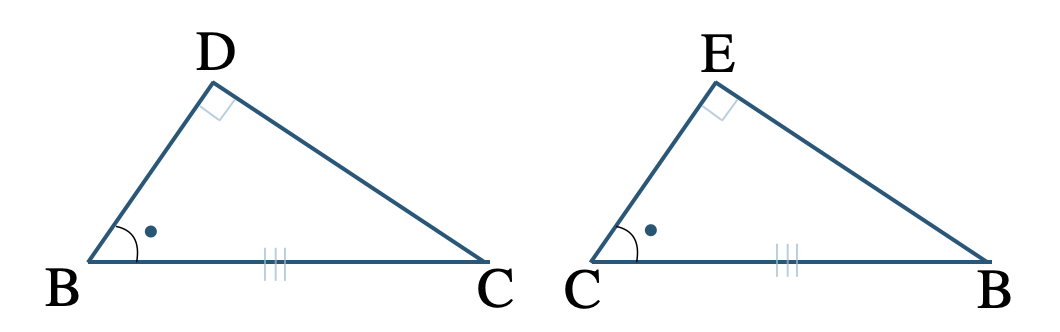
\(\angle{\rm BDC}=\angle{\rm CEB}=90^\circ\) (直角)
\({\rm BC=CB}\) (斜辺)
二等辺三角形の底角より、
\(\angle{\rm DBC}=\angle{\rm ECB}\)
よって、
\(\triangle {\rm DBC}\equiv\triangle {\rm ECB}\)
合同条件は、
直角三角形の斜辺と1つの鋭角がそれぞれ等しい
となる



