問題:平行四辺形の証明
次の証明をせよ。
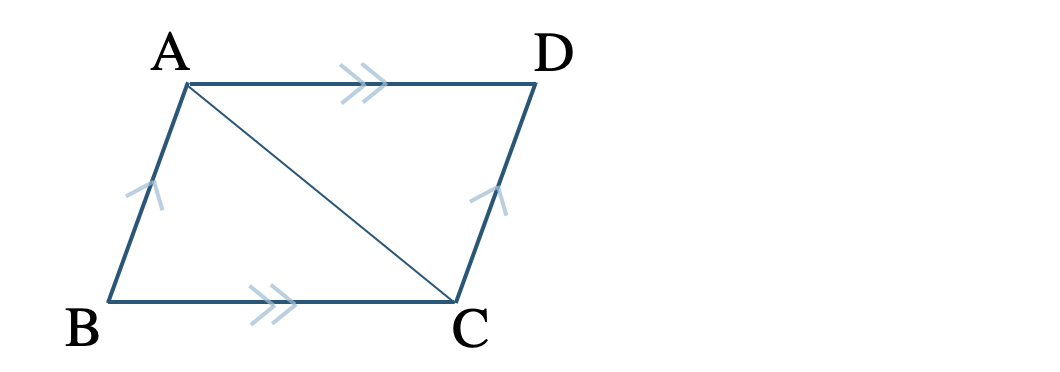
\({\small (1)}~\)平行四辺形の定理1と定理2を、対角線 \({\rm AC}\) をひくことで証明せよ。
【定理1】平行四辺形の対辺はそれぞれ等しい
【定理2】平行四辺形の対角はそれぞれ等しい
\({\small (2)}~\)平行四辺形の定理3を、対角線 \({\rm AC~,~BD}\) の交点 \({\rm O}\) をすることで証明せよ。
【定理3】平行四辺形の対角線はそれぞれの中点で交わる

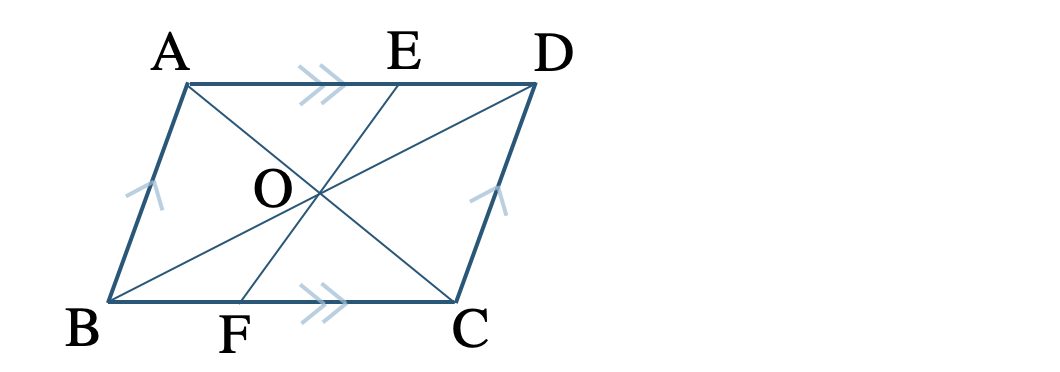
\({\small (3)}~\)▱ \({\rm ABCD}\)の対角線 \({\rm AC~,~BD}\) との交点を \({\rm O}\) として、この交点 \({\rm O}\) を通る直線と辺 \({\rm AD~,~BC}\) との交点を \({\rm E~,~F}\) とするとき、\({\rm OE=OF}\) であることを証明せよ。
解法のPoint
平行四辺形の性質を使った証明方法は、
証明を書き始める前に、見通しをたてる。
・証明する2つの三角形に着目する。
・仮定や仮定から導かれる根拠となることがらを考える。
平行四辺形の定義より、
\({\small (1)}~\)2組の対辺がそれぞれ平行
平行四辺形の定理より、
\({\small (2)}~\)対辺はそれぞれ等しい
\({\small (3)}~\)対角はそれぞれ等しい
\({\small (4)}~\)対角線はそれぞれの中点で交わる
・根拠より、合同条件を考える。
■ 証明のすすめ方
① 着目している三角形がどれとどれかを書く。
② 仮定から根拠となることがらを書く。
③ 仮定から導かられる根拠を書く。
④ 根拠から三角形の合同条件を書く。
⑤ 三角形が合同であることを記号 \(\equiv\) で表す。
⑥ 合同な図形の性質より、結論を導く。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:平行四辺形の証明
問題解説(1)
次の証明をせよ。
\({\small (1)}~\)平行四辺形の定理1と定理2を、対角線 \({\rm AC}\) をひくことで証明せよ。
【定理1】平行四辺形の対辺はそれぞれ等しい
【定理2】平行四辺形の対角はそれぞれ等しい

・\({\rm AB=CD~,~AD=BC}\) と \(\angle{\rm A}=\angle{\rm C}~,~\angle{\rm B}=\angle{\rm D}\) を示すために、\(\triangle {\rm ABC}\) と \(\triangle {\rm CDA}\) に着目する
・錯角より、\(\angle{\rm ACB}=\angle{\rm CAD}\)
・錯角より、\(\angle{\rm BAC}=\angle{\rm DCA}\)
・共通の辺より、\({\rm AC=CA}\)
・合同条件は、1組の辺とその両端の角がそれぞれ等しい
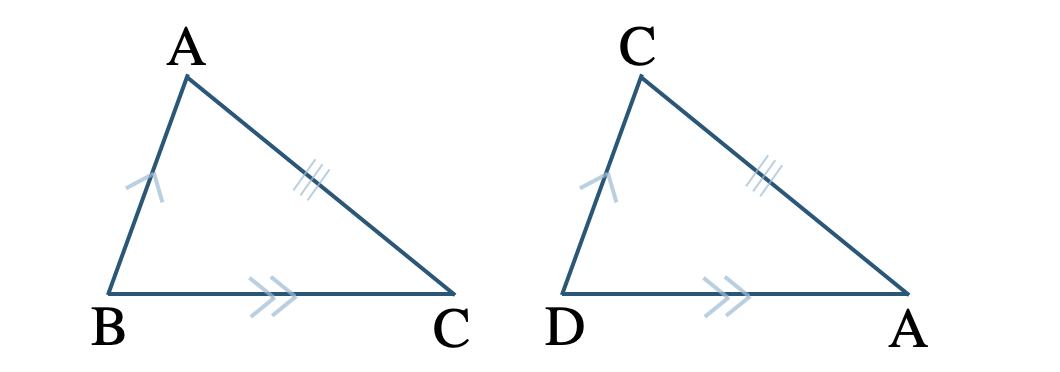
[証明] \(\triangle {\rm ABC}\) と \(\triangle {\rm CDA}\) において、
\({\rm AD\,//\,BC}\) より、錯角が等しいので、
\(\angle{\rm ACB}=\angle{\rm CAD}~~~\cdots{\large ①}\)
\({\rm AB\,//\,DC}\) より、錯角が等しいので、
\(\angle{\rm BAC}=\angle{\rm DCA}~~~\cdots{\large ②}\)
共通の辺より、
\({\rm AC=CA}~~~\cdots{\large ③}\)
①、②、③より、1組の辺とその両端の角がそれぞれ等しいから、
\(\triangle {\rm ABC}\equiv\triangle {\rm CDA}\)
合同な図形では対応する辺の長さ、角の大きさは等しいから、
\({\rm AB=CD~,~BC=DA}~~~\cdots{\large ④}\)
\(\angle{\rm ABC}=\angle{\rm CDA}~~~\cdots{\large ⑤}\)
④より、\({\rm AB=CD~,~AD=BC}\) となるので、
【定理1】平行四辺形の対辺はそれぞれ等しい
が示される
また、①と②より、$$\begin{eqnarray}~~~\angle{\rm BAC}+\angle{\rm DAC}&=&\angle{\rm ACD}+\angle{\rm DCA}\\[2pt]~~~\angle{\rm BAD}&=&\angle{\rm DCB}\\[2pt]~~~\angle{\rm A}&=&\angle{\rm C}\end{eqnarray}$$⑤より、\(\angle{\rm B}=\angle{\rm D}\) となるので、
【定理2】平行四辺形の対角はそれぞれ等しい
が示される [終]
問題解説(2)
次の証明をせよ。
\({\small (2)}~\)平行四辺形の定理3を、対角線 \({\rm AC~,~BD}\) の交点 \({\rm O}\) をすることで証明せよ。
【定理3】平行四辺形の対角線はそれぞれの中点で交わる

・\({\rm AO=CO~,~BO=DO}\) を示すために、\(\triangle {\rm AOB}\) と \(\triangle {\rm COD}\) に着目する
(※ \(\triangle {\rm AOD}\) と \(\triangle {\rm COB}\) でもよい。)
・定理より、\({\rm AB=CD}\)
・錯角より、\(\angle{\rm BAO}=\angle{\rm DCO}\)
・錯角より、\(\angle{\rm ABO}=\angle{\rm CDO}\)
・合同条件は、1組の辺とその両端の角がそれぞれ等しい
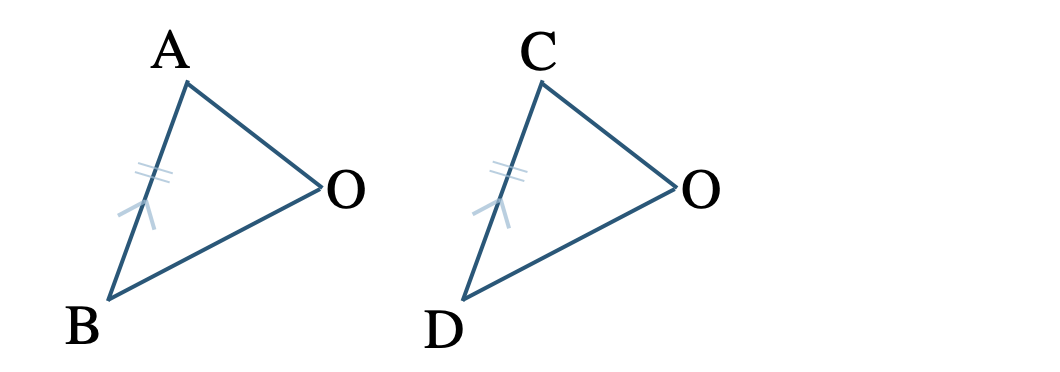
[証明] \(\triangle {\rm AOB}\) と \(\triangle {\rm COB}\) において、
平行四辺形の対辺は等しいので、
\({\rm AB=CD}~~~\cdots{\large ①}\)
平行四辺形の定義 \({\rm AB\,//\,DC}\) より、錯角が等しいので、
\(\angle{\rm BAO}=\angle{\rm DCO}~~~\cdots{\large ②}\)
\(\angle{\rm ABO}=\angle{\rm CDO}~~~\cdots{\large ③}\)
①、②、③より、1組の辺とその両端の角がそれぞれ等しいから、
\(\triangle {\rm AOB}\equiv\triangle {\rm COD}\)
合同な図形では対応する辺の長さは等しいから、
\({\rm AO=CO~,~BO=DO}\)
したがって、
【定理3】平行四辺形の対角線はそれぞれの中点で交わる
[終]
問題解説(3)
次の証明をせよ。
\({\small (3)}~\)▱ \({\rm ABCD}\)の対角線 \({\rm AC~,~BD}\) との交点を \({\rm O}\) として、この交点 \({\rm O}\) を通る直線と辺 \({\rm AD~,~BC}\) との交点を \({\rm E~,~F}\) とするとき、\({\rm OE=OF}\) であることを証明せよ。

・\({\rm OE=OF}\) を示すために、\(\triangle {\rm OBF}\) と \(\triangle {\rm ODE}\) に着目する
・仮定より、\({\rm BF=DE}\)
・定理より、\({\rm OB=OD}\)
・錯角より、\(\angle{\rm OBF}=\angle{\rm ODE}\)
・合同条件は、2組の辺とその間の角がそれぞれ等しい
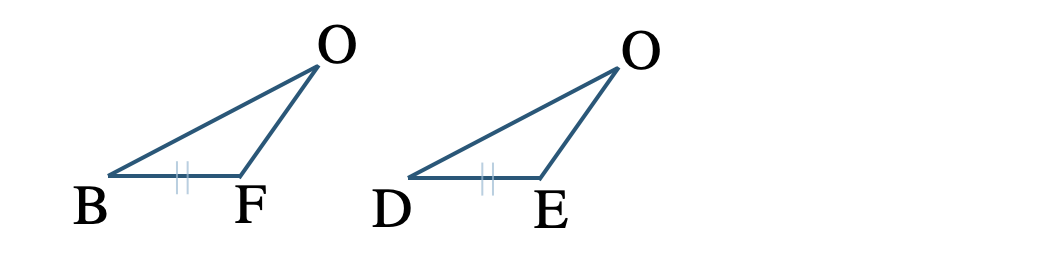
[証明] \(\triangle {\rm OBF}\) と \(\triangle {\rm ODE}\) において、
仮定より、
\({\rm BF=DF}~~~\cdots{\large ①}\)
平行四辺形の対角線はそれぞれの中点で交わるので、
\({\rm OB=OD}~~~\cdots{\large ②}\)
平行四辺形の定義 \({\rm BC\,//\,AD}\) より、錯角が等しいので、
\(\angle{\rm OBF}=\angle{\rm ODE}~~~\cdots{\large ③}\)
①、②、③より、2組の辺とその間の角がそれぞれ等しいから、
\(\triangle {\rm OBF}\equiv\triangle {\rm ODE}\)
合同な図形では対応する辺の長さは等しいから、
\({\rm OE=OF}\)
[終]



