図形の中の平行四辺形の解法
四角形が平行四辺形となることの証明方法は、
証明を書き始める前に、見通しをたてる。
・着目する四角形について、仮定よりわかっていることを書きこむ。
→もとの平行四辺形の定義や定理を利用する。
・平行四辺形となるための条件を考える。
\({\small (1)}~\)2組の対辺がそれぞれ平行である
\({\small (2)}~\)2組の対辺がそれぞれ等しい
\({\small (3)}~\)2組の対角がそれぞれ等しい
\({\small (4)}~\)対角線がそれぞれの中点で交わる
\({\small (5)}~\)1組の対辺が等しくて平行である
■ 証明のすすめ方
① もとの平行四辺形の定義や定理より、根拠となることがらを書く。
② 仮定から導かられる根拠を書く。
③ 根拠から平行四辺形になるための条件を書き、四角形が平行四辺形であることを表す。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:図形の中の平行四辺形
問題解説(1)
次の証明をせよ。
\({\small (1)}~\)▱ \({\rm ABCD}\) の対角線 \({\rm BD}\) 上に、\({\rm BE=DF}\) となるように点 \({\rm E~,~F}\) をとる。
このとき、四角形 \({\rm AECF}\) が平行四辺形となることを示せ。
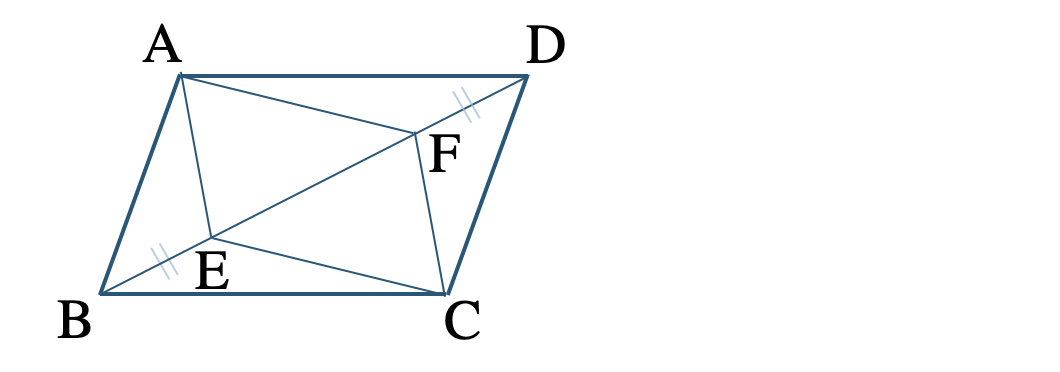
・四角形 \({\rm AECF}\) が平行四辺形となることを示すために、条件「対角線かそれぞれの中点で交わる」を示す。
・▱ \({\rm ABCD}\) より、
\({\rm AO=CO~,~BO=DO}\)
・仮定より、\({\rm BE=DF}\)
・根拠は、\({\rm AO=OC~,~EO=FO}\)

[証明] 対角線の交点を \({\rm O}\) として、▱ \({\rm ABCD}\) の対角線がそれぞれの中点で交わるので、
\({\rm AO=CO}~~~\cdots{\large ①}\)
\({\rm BO=DO}~~~\cdots{\large ②}\)
仮定より、
\({\rm BE=DF}~~~\cdots{\large ③}\)
②と③より、
\(\begin{eqnarray}~~~{\rm BO-BE}&=&{\rm DO-DF}\\[2pt]~~~{\rm EO}&=&{\rm FO}~~~\cdots{\large ④}\end{eqnarray}\)
①と④より、対角線がそれぞれの中点で交わるので、
四角形 \({\rm AECF}\) が平行四辺形となる
[終]
問題解説(2)
次の証明をせよ。
\({\small (2)}~\)▱ \({\rm ABCD}\) について、辺 \({\rm AD~,~BC}\) の中点をそれぞれ \({\rm E~,~F}\) とする。
このとき、四角形 \({\rm AFCE}\) が平行四辺形となることを示せ。
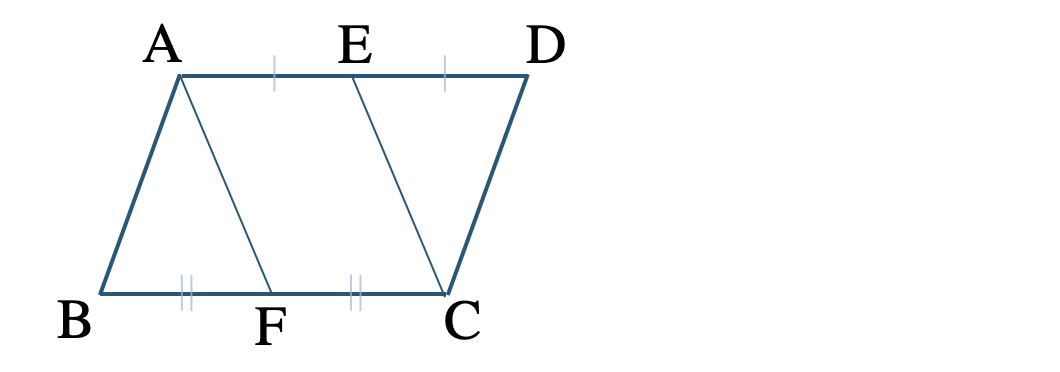
・四角形 \({\rm AFCE}\) が平行四辺形となることを示すために、条件「1組の対辺が等しくて平行である」を示す。
・▱ \({\rm ABCD}\) より、
\({\rm AD\,//\,BC~,~AD=BC}\)
・仮定より、\({\rm AE={\large \frac{\,1\,}{\,2\,}}AD~,~FC={\large \frac{\,1\,}{\,2\,}}BC}\)
・根拠は、\({\rm AE\,//\,FC~,~AE=FC}\)
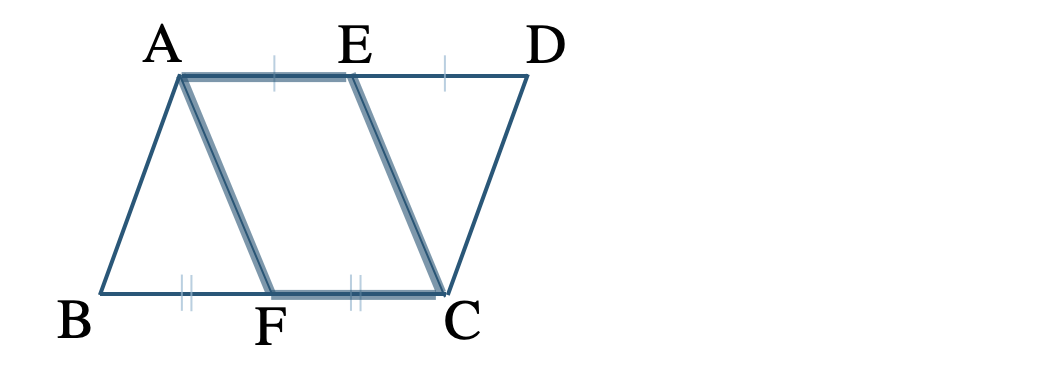
[証明] ▱ \({\rm ABCD}\) の対辺は平行で長さが等しいので、
\({\rm AD\,//\,BC}~~~\cdots{\large ①}\)
\({\rm AD=BC}~~~\cdots{\large ②}\)
①より、
\({\rm AE\,//\,FC}~~~\cdots{\large ③}\)
仮定より、点 \({\rm E~,~F}\) は辺 \({\rm AD~,~BC}\) の中点であるので、
\(\begin{split}~~~{\rm AE}=\frac{\,1\,}{\,2\,}{\rm AD}~,~{\rm FC}=\frac{\,1\,}{\,2\,}{\rm BC}\end{split}\)
これと②より、
\({\rm AE=FC}~~~\cdots{\large ④}\)
③と④より、1組の対辺が等しくて平行であるので、
四角形 \({\rm AFCE}\) が平行四辺形となる
[終]
問題解説(3)
次の証明をせよ。
\({\small (3)}~\)▱ \({\rm ABCD}\) の辺 \({\rm AB~,~CD}\) 上に \(\angle{\rm AED}=\angle{\rm CFB}\) となるように点 \({\rm E~,~F}\) をとる。
このとき、四角形 \({\rm EBFD}\) が平行四辺形となることを示せ。
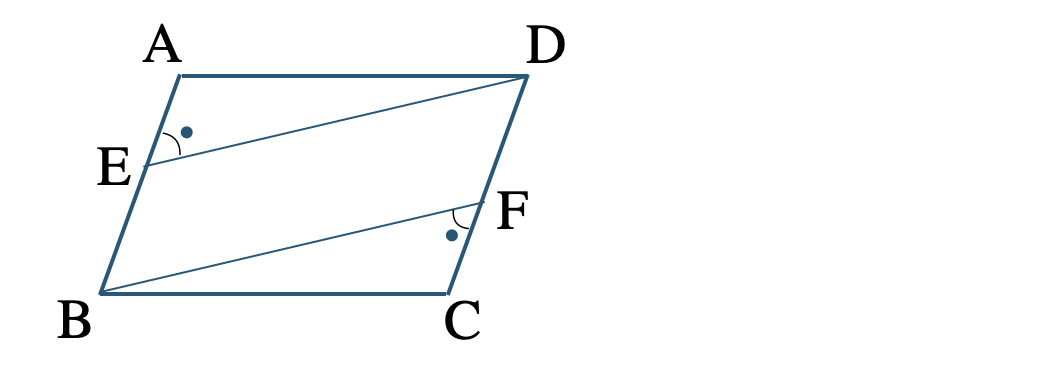
・四角形 \({\rm EBFD}\) が平行四辺形となることを示すために、条件「2組の対角がそれぞれ等しい」を示す。
・▱ \({\rm ABCD}\) より、
\(\angle{\rm EAD}=\angle{\rm FCB}\)
\(\angle{\rm ADC}=\angle{\rm CBA}\)
・仮定より、\(\angle{\rm AED}=\angle{\rm CFB}\)
・根拠は、
\(\angle{\rm EDF}=\angle{\rm FBE}\)
\(\angle{\rm DEB}=\angle{\rm BFD}\)

[証明] ▱ \({\rm ABCD}\) の2組の対角がそれぞれ等しいので、
\(\angle{\rm EAD}=\angle{\rm FCB}~~~\cdots{\large ①}\)
\(\angle{\rm ADC}=\angle{\rm CBA}~~~\cdots{\large ②}\)
仮定より、
\(\angle{\rm AED}=\angle{\rm CFB}~~~\cdots{\large ③}\)
①と③より、三角形の内角の和が \(180^\circ\) であるので、
\(\angle{\rm ADE}=\angle{\rm CBF}\)
これと②より、
\(\angle{\rm EDF}=\angle{\rm FBE}~~~\cdots{\large ④}\)
また、③より、
\(\angle{\rm DEB}=\angle{\rm BFD}~~~\cdots{\large ⑤}\)
④と⑤より、2組の対角がそれぞれ等しいので、
四角形 \({\rm EBFD}\) が平行四辺形となる
[終]



