今回の問題は「硬貨を投げる確率」です。
\(~\)数研出版 これからの数学2 p.193 問1~2
\(~\)東京書籍 新しい数学2 p.166 問3
\(~\)啓林館 未来へひろがる数学2 p.164~165 問3~5
問題
\({\small (1)}~\)\(2\) 枚の硬貨を同時に投げるとき、次の確率を求めよ。
① \(2\) 枚とも表の確率
② \(1\) 枚が表で \(1\) 枚が裏の確率
\({\small (2)}~\)\(3\) 枚の硬貨を同時に投げるとき、次の確率を求めよ。
① \(3\) 枚とも裏の確率
② \(1\) 枚が表で \(2\) 枚が裏の確率
③ 少なくとも \(1\) 枚が裏の確率
次の問いに答えよ。
\({\small (1)}~\)\(2\) 枚の硬貨を同時に投げるとき、次の確率を求めよ。
① \(2\) 枚とも表の確率
② \(1\) 枚が表で \(1\) 枚が裏の確率
\({\small (2)}~\)\(3\) 枚の硬貨を同時に投げるとき、次の確率を求めよ。
① \(3\) 枚とも裏の確率
② \(1\) 枚が表で \(2\) 枚が裏の確率
③ 少なくとも \(1\) 枚が裏の確率
Point:硬貨を投げる確率
① \(2\) 枚以上の硬貨を投げるときは、それらをA、B、C、…と区別して考える。
② 表を◯、裏を×として樹形図を描く。
たとえば、\(2\) 枚の硬貨A、Bでは、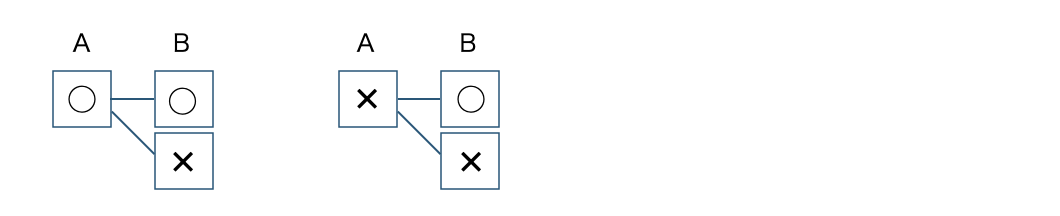
\(3\) 枚の硬貨A、B、Cでは、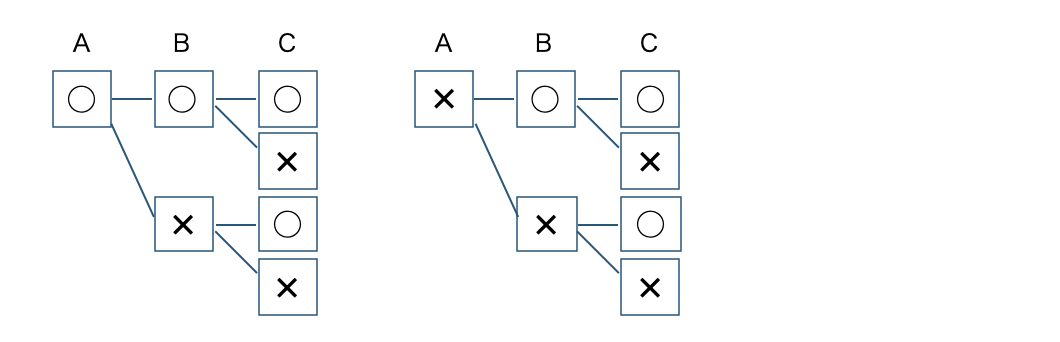
③ 条件に合う場合の数を数えて、確率を求める。
硬貨を投げる確率の求め方は、
① \(2\) 枚以上の硬貨を投げるときは、それらをA、B、C、…と区別して考える。
② 表を◯、裏を×として樹形図を描く。
たとえば、\(2\) 枚の硬貨A、Bでは、

この \(4\) 通りの起こり方は同様に確からしい
\(3\) 枚の硬貨A、B、Cでは、

この \(8\) 通りの起こり方は同様に確からしい
③ 条件に合う場合の数を数えて、確率を求める。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
Point:起こらない確率
「Aが起こらない確率」などはそれが起こる確率を求めて、
(起こらない確率)=1 ー (起こる確率)
また、「少なくとも1回Aが出る確率」は、
1 ー (Aが1回も出ない確率)
たとえば、さいころを1回投げて、1の目が出ない確率は、
\(\begin{split}~~~1-\frac{\,1\,}{\,6\,}=\frac{\,5\,}{\,6\,}\end{split}\)
起こらない確率の求め方は、
「Aが起こらない確率」などはそれが起こる確率を求めて、
(起こらない確率)=1 ー (起こる確率)
を使って計算する。
また、「少なくとも1回Aが出る確率」は、
1 ー (Aが1回も出ない確率)
たとえば、さいころを1回投げて、1の目が出ない確率は、
\(\begin{split}~~~1-\frac{\,1\,}{\,6\,}=\frac{\,5\,}{\,6\,}\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
次のページ「解法のPointと問題解説」


