問題:くじ引きの確率
問題
\({\small (1)}~\)Aさんがあたる確率
\({\small (2)}~\)Bさんがあたる確率
5本中2本があたりのくじがある。AさんとBさんがこの順にくじを1本ずつ引いていく。ただし、引いたくじは元に戻さない。このとき、次の確率を求めよ。
\({\small (1)}~\)Aさんがあたる確率
\({\small (2)}~\)Bさんがあたる確率
解法のPoint
Point:くじ引きの確率
① くじをすべて区別して考える。
あたりを◯、はずれを●として5本のくじは、
① ② ③ ❹ ❺
と区別される。
② 選んで並べるパターンとして樹形図をかく。
AさんとBさんがこの順にくじを1本ずつ引くので、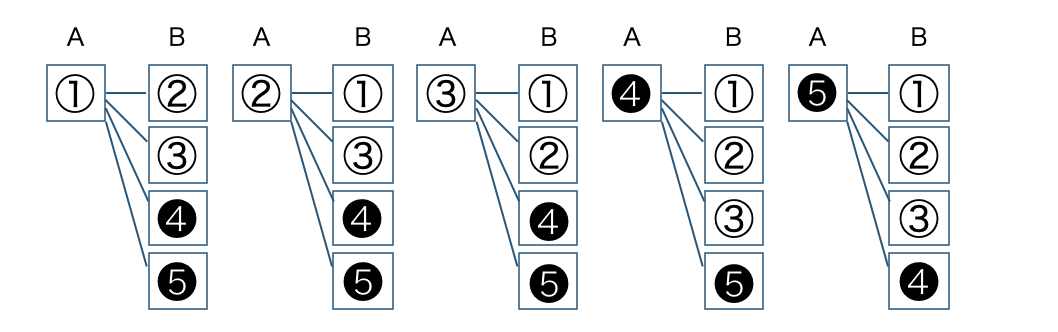
Aさんが当たる確率は、\(\begin{split}\frac{\,3\,}{\,5\,}\end{split}\)
Bさんが当たる確率は、樹形図より、
\(\begin{split}~~~\frac{\,12\,}{\,20\,}=\frac{\,3\,}{\,5\,}\end{split}\)
5本中3本があたりのくじがある。AさんとBさんがこの順にくじを1本ずつ引いていく。ただし、引いたくじは元に戻さない。
① くじをすべて区別して考える。
あたりを◯、はずれを●として5本のくじは、
① ② ③ ❹ ❺
と区別される。
② 選んで並べるパターンとして樹形図をかく。
AさんとBさんがこの順にくじを1本ずつ引くので、

③ 樹形図より確率を求める。
Aさんが当たる確率は、\(\begin{split}\frac{\,3\,}{\,5\,}\end{split}\)
Bさんが当たる確率は、樹形図より、
\(\begin{split}~~~\frac{\,12\,}{\,20\,}=\frac{\,3\,}{\,5\,}\end{split}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:くじ引きの確率
問題解説(1)
問題
\({\small (1)}~\)Aさんがあたる確率
5本中2本があたりのくじがある。AさんとBさんがこの順にくじを1本ずつ引いていく。ただし、引いたくじは元に戻さない。このとき、次の確率を求めよ。
\({\small (1)}~\)Aさんがあたる確率
あたりを◯、はずれを●として5本のくじは、
① ② ❸ ❹ ❺
と区別される
Aさんがあたる確率は、
起こりうるすべての場合の数は、\(5\) 通りで同様に確からしい
また、あたりは①か②の \(2\) 通りである
よって、確率は \(\begin{split}{\frac{\,2\,}{\,5\,}}\end{split}\) となる
問題解説(2)
問題
\({\small (2)}~\)Bさんがあたる確率
5本中2本があたりのくじがある。AさんとBさんがこの順にくじを1本ずつ引いていく。ただし、引いたくじは元に戻さない。このとき、次の確率を求めよ。
\({\small (2)}~\)Bさんがあたる確率
あたりを◯、はずれを●として5本のくじは、
① ② ❸ ❹ ❺
と区別される
AさんとBさんがこの順にくじを1本ずつ引くので、選んで並べるパターンの樹形図をかくと、
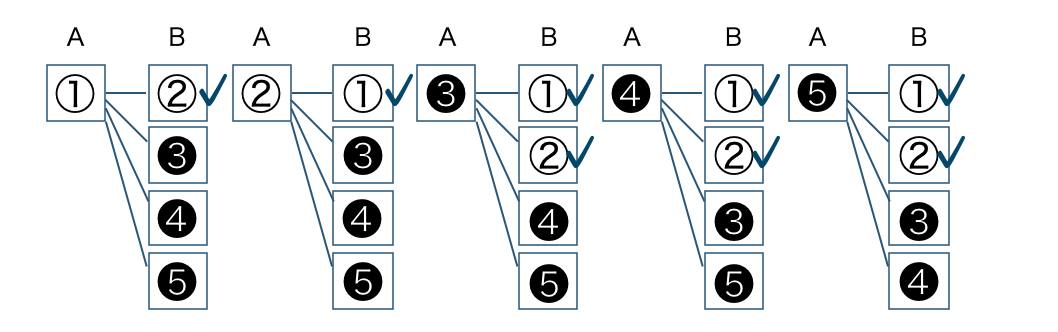
起こりうるすべての場合の数は、\(4\times5=20\) 通りで、同様に確からしい
また、Bさんがあたるのは✓を付けた \(8\) 通りであるので、確率は、
\(\begin{split}~~~\frac{\,8\,}{\,20\,}=\frac{\,2\,}{\,5\,}\end{split}\)
したがって、答えは \(\begin{split}{\frac{\,2\,}{\,5\,}}\end{split}\) となる
※ この結果より、くじ引きでは順番に関係なくあたる確率は同じである

【問題一覧】中2|確率
このページは「中学数学2 確率」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こ...


