今回の問題は「四分位数と四分位範囲」です。
\(~\)数研出版 これからの数学2 p.172~176 問1~5
\(~\)東京書籍 新しい数学2 p.180~181
\(~\)啓林館 未来へひろがる数学2 p.174~177 問1~4
問題
\({\small (1)}~\)データA
\(~~~5~,~12~,~14~,~20~,~22~,~26~,~27~,~33~,~35\)
\({\small (2)}~\)データB
\(\begin{eqnarray}~~~&10~,~11~,~16~,~16~,~18\\[2pt]~~~&22~,~24~,~25~,~30~,~32\end{eqnarray}\)
\({\small (3)}~\)それぞれの四分位範囲を比べて、どちらが散らばりが大きいか答えよ。
次のデータの最小値、最大値、範囲、中央値、四分位数と四分位範囲をそれぞれ求めよ。
\({\small (1)}~\)データA
\(~~~5~,~12~,~14~,~20~,~22~,~26~,~27~,~33~,~35\)
\({\small (2)}~\)データB
\(\begin{eqnarray}~~~&10~,~11~,~16~,~16~,~18\\[2pt]~~~&22~,~24~,~25~,~30~,~32\end{eqnarray}\)
\({\small (3)}~\)それぞれの四分位範囲を比べて、どちらが散らばりが大きいか答えよ。
Point:データの最大値・最小値・範囲

データを小さい順に並べたとき、

一番小さい値を「最小値」、
一番大きい値を「最大値」、
最大値-最小値の値を「範囲」という。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
Point:四分位数と四分位範囲
■ データの個数が偶数の場合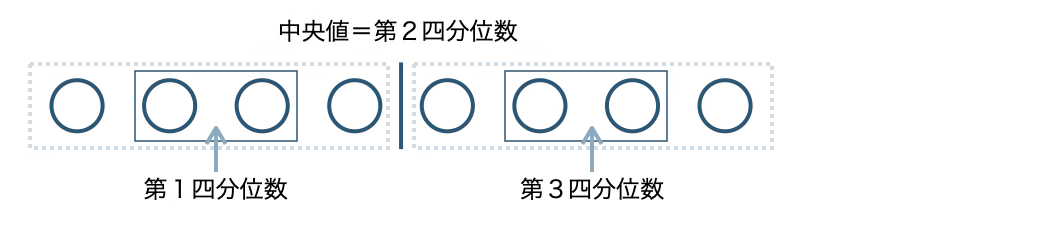
また、この第3四分位数ー第1四分位数の値を「四分位範囲」という。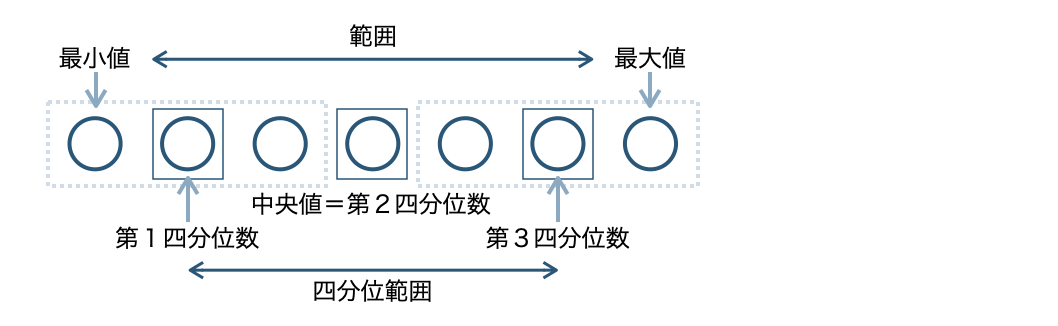
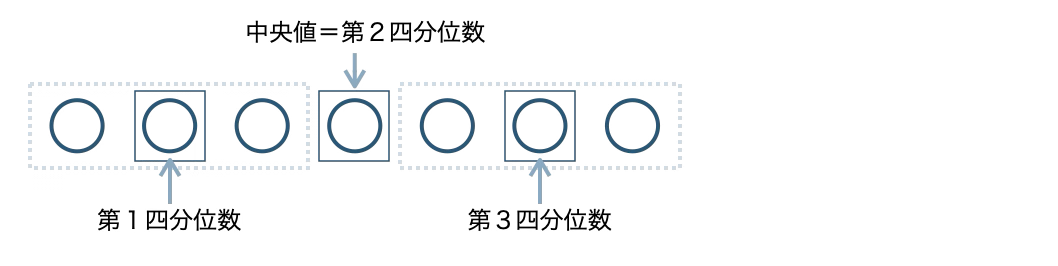
■ データの個数が奇数の場合

データの真ん中の値を「中央値」または「第2四分位数」といい、中央値以外の、
小さい組の真ん中の値を「第1四分位数」
大きい組の真ん中の値を「第3四分位数」
■ データの個数が偶数の場合

データの真ん中の2つの値の平均値を「中央値」または「第2四分位数」といい、
全体を2つに分けたときの、
小さい組の真ん中の値を「第1四分位数」
大きい組の真ん中の値を「第3四分位数」
また、この第3四分位数ー第1四分位数の値を「四分位範囲」という。

©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
次のページ「解法のPointと問題解説」


