問題:箱ひげ図
次の問いに答えよ。
\({\small (1)}~\)次のデータの箱ひげ図をかけ。
\(\begin{eqnarray}~~~&6~,~8~,~9~,~10~,~12~,~15\\[2pt]~~~&16~,~18~,~19~,~22~,~23\end{eqnarray}\)
\({\small (2)}~\)次の図は、A、B、Cそれぞれ \(20\) 個のデータを分布させた箱ひげ図である。
次の問いに答えよ。
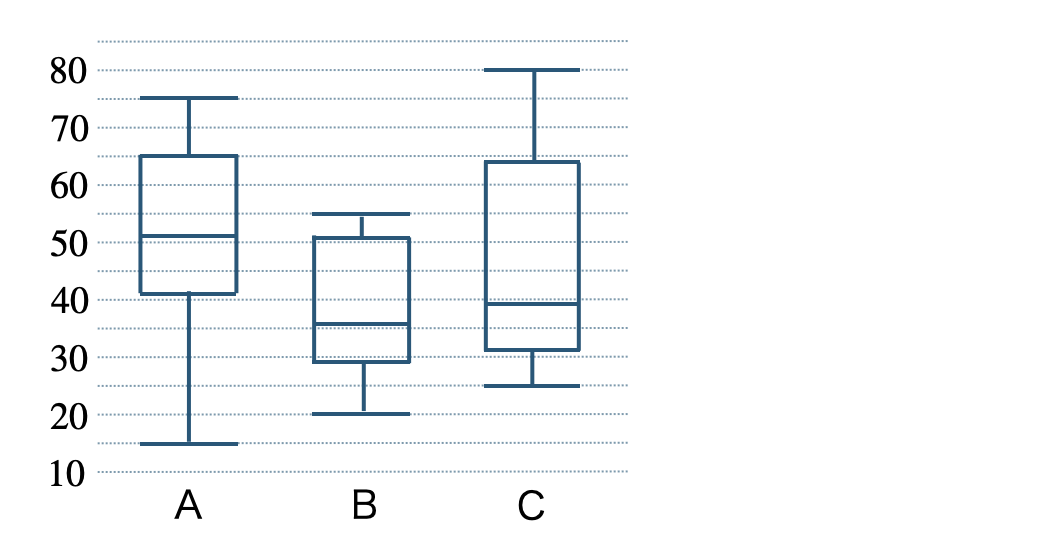
① 最大値が一番大きいデータは?
② 最小値が一番小さいデータは?
③ 範囲が一番大きいデータは?
④ 四分位範囲が一番大きいデータは?
⑤ \(40\) 点以上の数が一番多いデータは?
⑥ \(30\) 点以下の数が一番多いデータは?
⑦ この箱ひげ図から平均値は読み取れるか答えよ。
解法のPoint
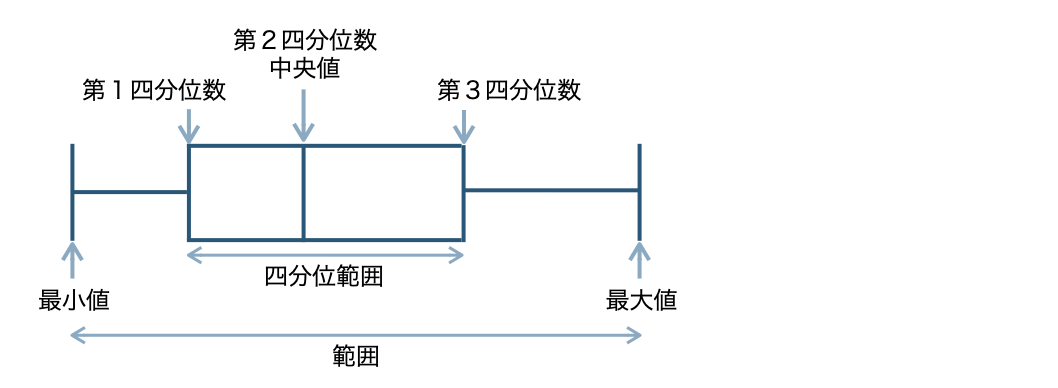
■ 箱ひげ図
データの最小値、最大値、四分位数を分布させたものを「箱ひげ図」といい、真ん中の長方形を「箱」、左右の部分を「ひげ」という。
① ひげの両端に最大値と最小値をつくる。
② 箱の両端が第1四分位数と第3四分位数であり、中央値=第2四分位数を箱の中の仕切りとしてかく。
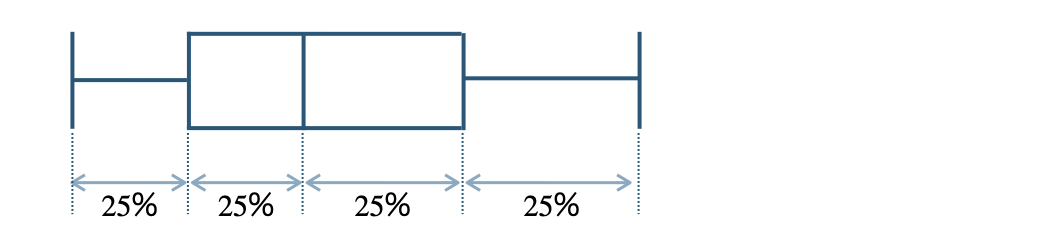
※ 4つに分けられた部分はそれぞれデータの個数の \(25\) %をふくむ。
この箱ひげ図を比べることで、いろいろな事を読み取れる。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:箱ひげ図
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)次のデータの箱ひげ図をかけ。
\(\begin{eqnarray}~~~&6~,~8~,~9~,~10~,~12~,~15\\[2pt]~~~&16~,~18~,~19~,~22~,~23\end{eqnarray}\)
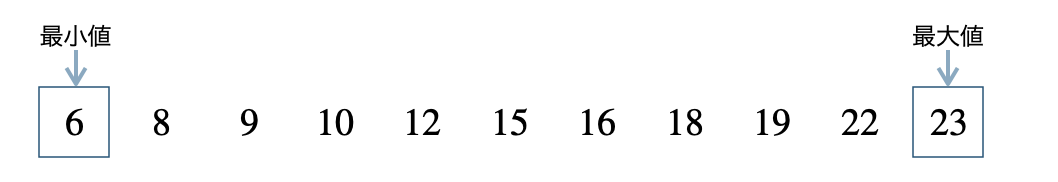
一番小さい値 \(6\) が最小値、
一番大きい値 \(23\) が最大値、
また、個数が \(11\) 個で奇数個あるので、

これより、中央値は真ん中の値の \(15\) となり、
第2四分位数も \(15\) となる

また、最小値をふくむ組の真ん中の値 \(9\) が第1四分位数となり、最大値をふくむ組の真ん中の値 \(19\) が第3四分位数となる
これより、箱ひげ図をかくと、
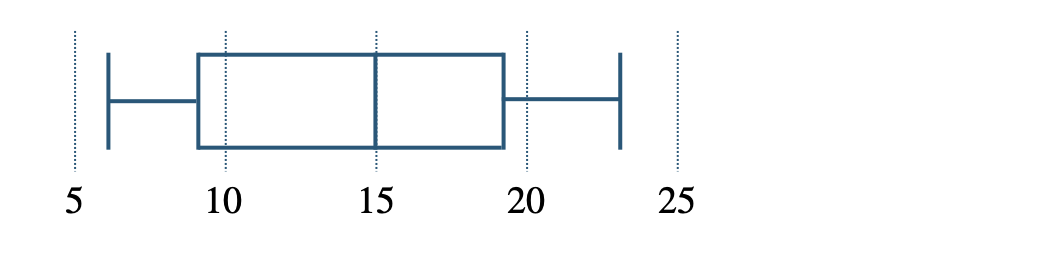
となる
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)次の図は、A、B、Cそれぞれ \(20\) 個のデータを分布させた箱ひげ図である。
次の問いに答えよ。

① 最大値が一番大きいデータは?
② 最小値が一番小さいデータは?
③ 範囲が一番大きいデータは?
④ 四分位範囲が一番大きいデータは?
⑤ \(40\) 点以上の数が一番多いデータは?
⑥ \(30\) 点以下の数が一番多いデータは?
⑦ この箱ひげ図から平均値は読み取れるか答えよ。
① それぞれの最大値を読み取ると、
A \(75\)、B \(55\)、C \(80\)
これより、答えは C となる
② それぞれの最小値を読み取ると、
A \(15\)、B \(20\)、C \(25\)
これより、答えは A となる
③ それぞれの範囲を求めると、
A \(75-15=60\)
B \(55-20=35\)
C \(80-25=55\)
これより、答えは A となる
また、箱ひげ図から範囲を読み取ると、

これより、答えは A となる
④ 箱ひげ図から四分位範囲を読み取ると、
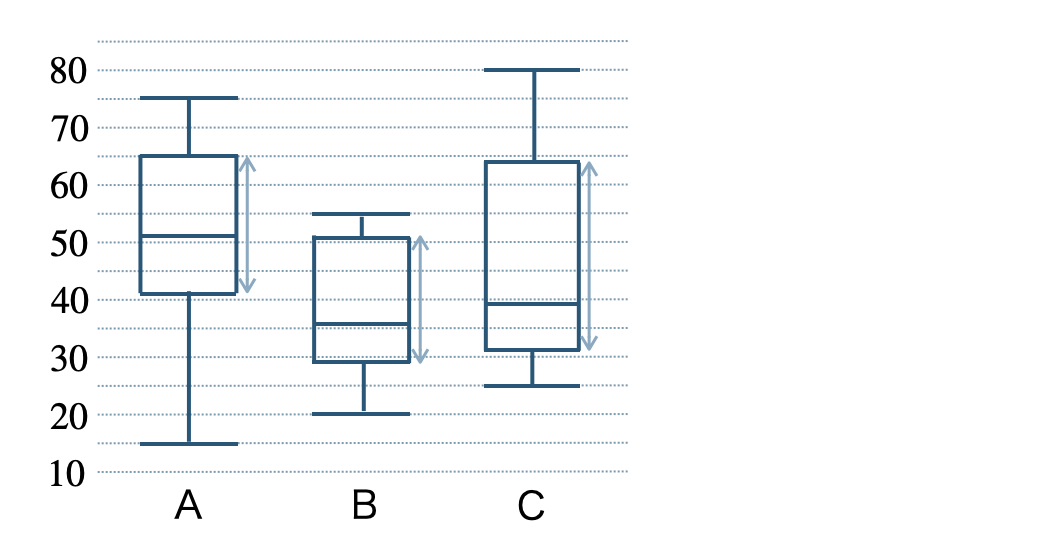
これより、答えは C となる
⑤ 箱ひげ図より、\(40\) 点のラインより上を読み取ると、
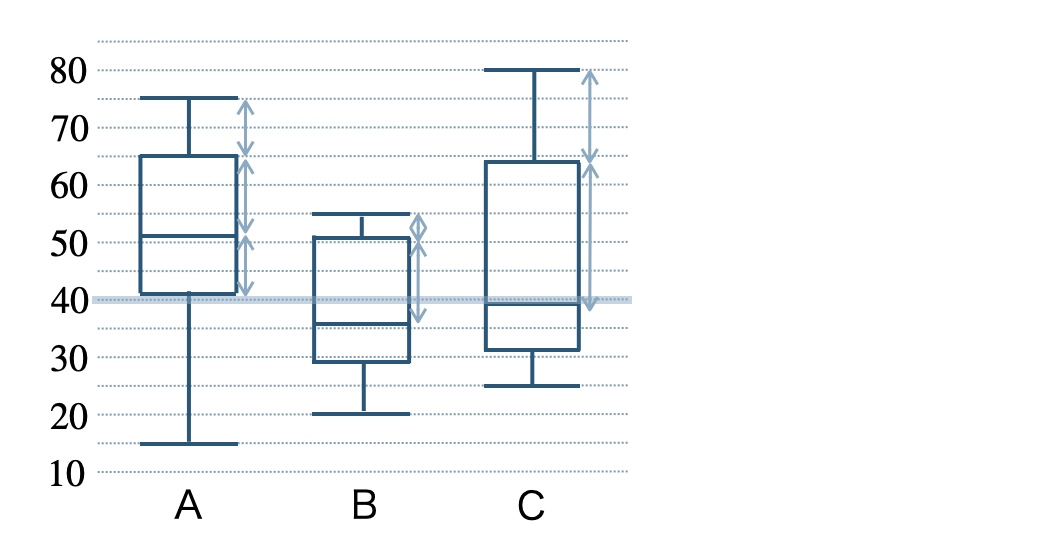
Aは全体の \(75\) %と少し
Bは全体の \(25\) %と少し
Cは全体の \(25\) %と少し
よって、\(40\) 点以上の数が一番多いのは A となる
⑥ 箱ひげ図より、\(30\) 点のラインより下を読み取ると、
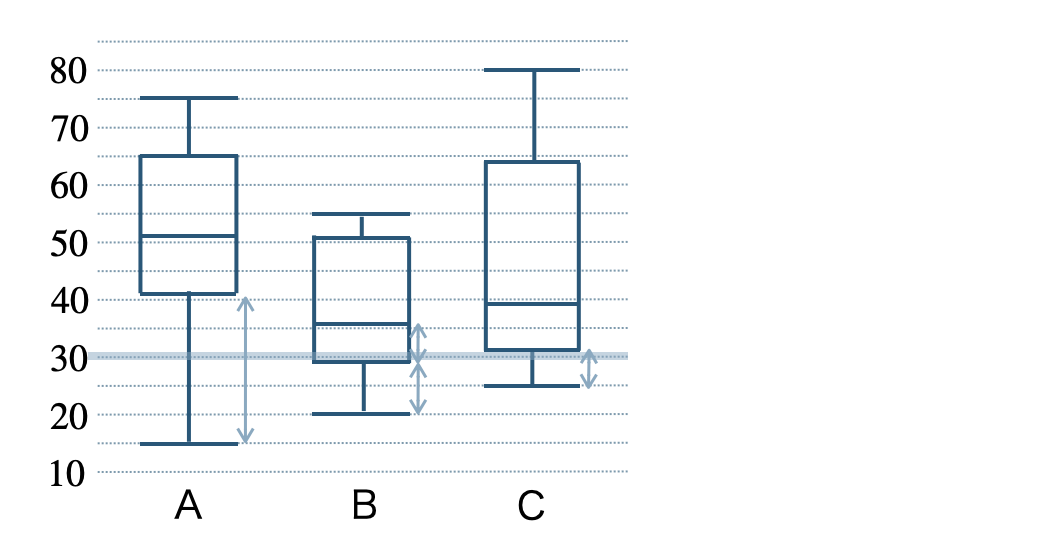
Aは全体の \(25\) %より小さい
Bは全体の \(25\) %と少し
Cは全体の \(25\) %より小さい
よって、\(30\) 点以下の数が一番多いのは B となる
⑦ この箱ひげ図からは、最小値、最大値、中央値や四分位数は読み取れるが、平均値は読み取れない



