2次方程式と道幅の解法
Point:2次方程式と道幅
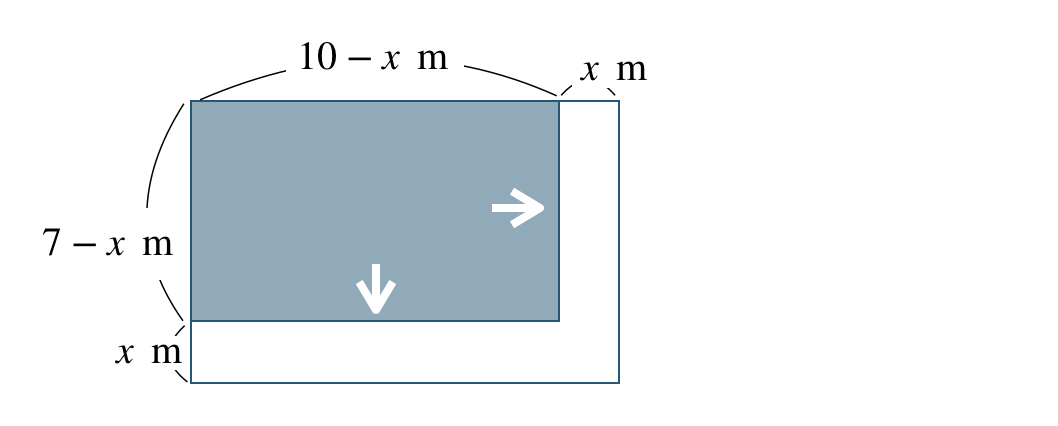
残りの土地の面積が \(40~{\rm m}^2\) より、
\(\begin{split}~~~(7-x)(10-x)=40\end{split}\)
③ 2次方程式を解く。
④ 解が問題に適していることを確認する。
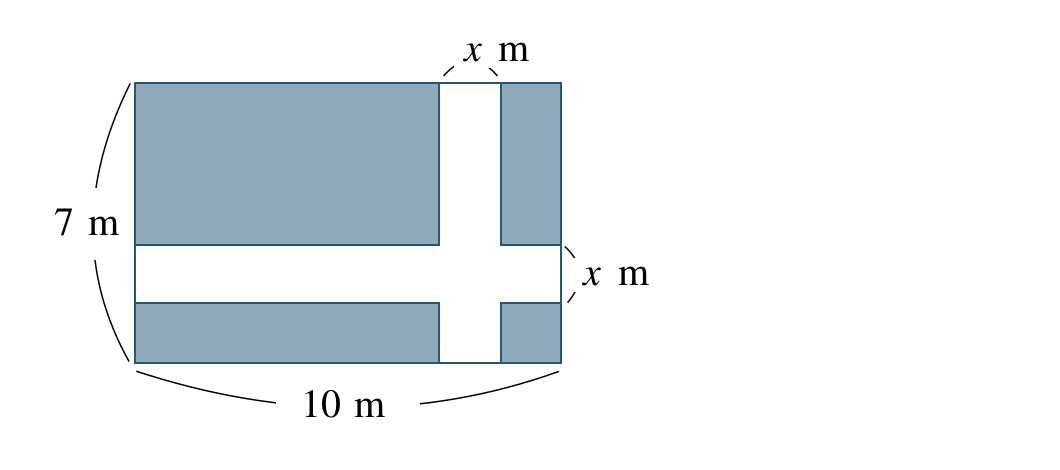
縦 \(7~{\rm m}\)、横 \(10~{\rm m}\) の土地に道幅 \(x~{\rm m}\) の道を上下左右に通すと残りの土地の面積が \(40~{\rm m}^2\) となった、道幅 \(x~{\rm m}\) の求め方は、

① 道を端に移動させて、残りの土地の縦と横の長さを求める。

② 残りの土地の面積より、2次方程式を立てる。
残りの土地の面積が \(40~{\rm m}^2\) より、
\(\begin{split}~~~(7-x)(10-x)=40\end{split}\)
③ 2次方程式を解く。
④ 解が問題に適していることを確認する。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:2次方程式と道幅
問題
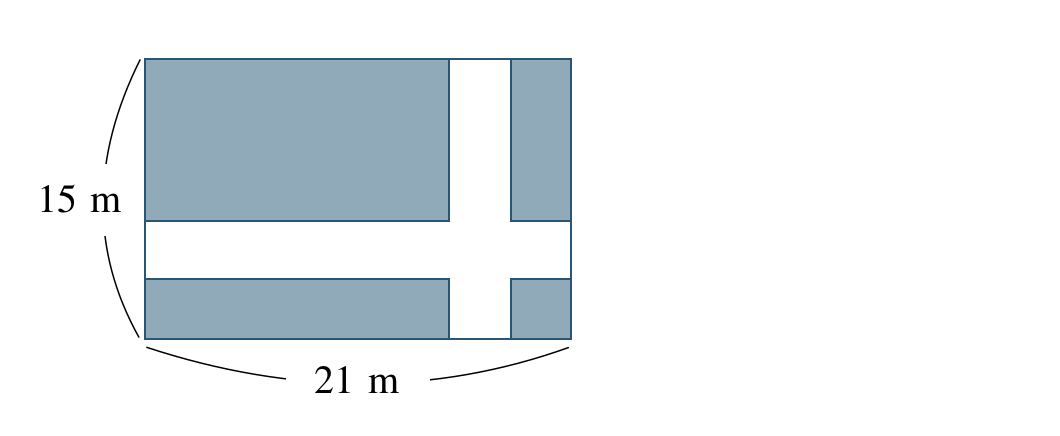
縦の長さが \(15~{\rm m}\)、横の長さが \(21~{\rm m}\) の長方形の土地に図のように道幅が同じで垂直に交わる道を2本つくり、残りの土地を花だんとした。
花だんとした土地の面積を \(280~{\rm m}^2\) とするとき、道幅は何 \({\rm m}\) となるか答えよ。

道幅を \(x~{\rm m}\) として、道を端に移動させると、
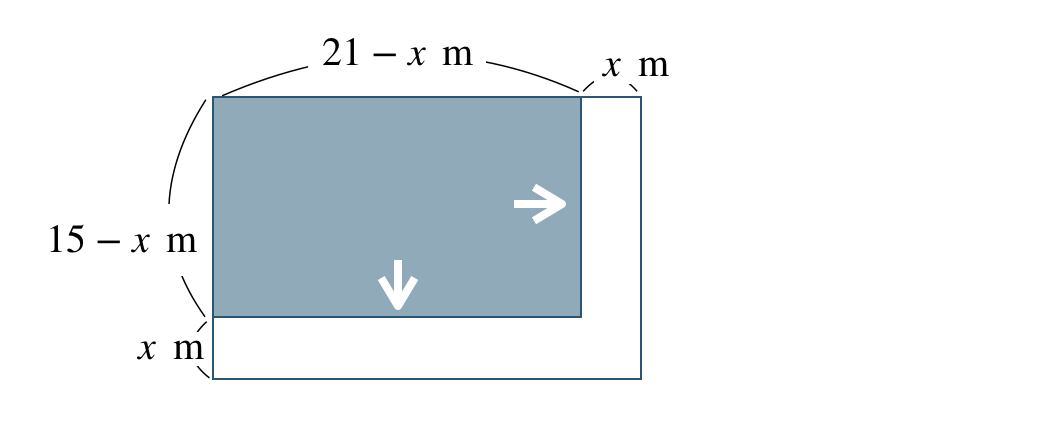
土地の面積 \(280~{\rm m}^2\) は縦の長さ \(15-x~{\rm m}\)、横の長さ \(21-x~{\rm m}\) より、
\(\begin{split}~~~(15-x)(21-x)=280\end{split}\)
この2次方程式を解くと、
\(\begin{eqnarray}~~~315-36x+x^2-280&=&0\\[2pt]~~~x^2-36x+35&=&0\\[2pt]~~~(x-1)(x-35)&=&0\\[2pt]~~~x&=&1~,~35\end{eqnarray}\)
\(0< x <15\) でなければならないので、
※ 道幅は \(0\) より大きく、もとの土地の縦の長さ \(15\) より小さい
\(x=35\) は問題は適してない
\(x=1\) は問題に適している
したがって、答えは \(1~{\rm m}\) となる
\(\begin{split}~~~(15-x)(21-x)=280\end{split}\)
この2次方程式を解くと、
\(\begin{eqnarray}~~~315-36x+x^2-280&=&0\\[2pt]~~~x^2-36x+35&=&0\\[2pt]~~~(x-1)(x-35)&=&0\\[2pt]~~~x&=&1~,~35\end{eqnarray}\)
\(0< x <15\) でなければならないので、
※ 道幅は \(0\) より大きく、もとの土地の縦の長さ \(15\) より小さい
\(x=35\) は問題は適してない
\(x=1\) は問題に適している
したがって、答えは \(1~{\rm m}\) となる

【問題一覧】中3|2次方程式
このページは「中学数学3 2次方程式」の問題一覧ページとなります。解説の見たい単元名がわからないとき...


