三角形と線分の比の解法
Point:三角形と線分の比
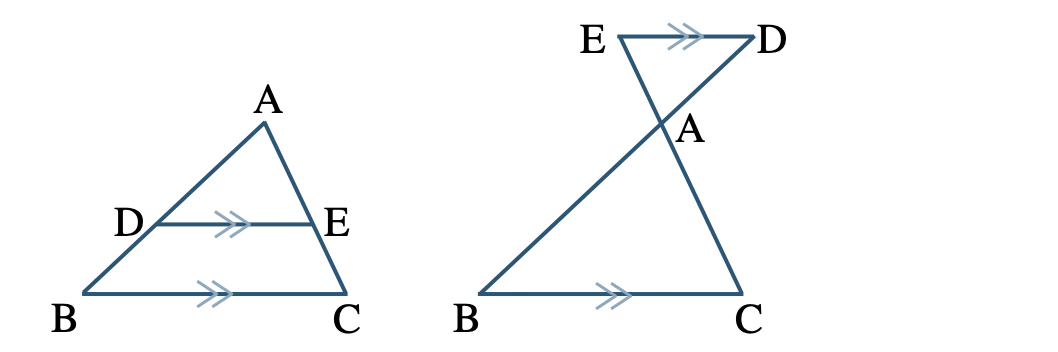
\({\rm AD:AB=AE:AC=DE:BC}\)
※ \(\triangle {\rm ADE}\,\,\unicode{x223D}\,\,\triangle {\rm ABC}\) より、対応する辺の比が等しい。
※ \({\rm AB~,~AC}\) の延長線上に点 \({\rm D~,~E}\) があっても成り立つ。
\({\small (2)}~\)\({\rm DE\,//\,BC}\) ならば、
\({\rm AD:DB=AE:EC}\)

\(\triangle {\rm ABC}\) の辺 \({\rm AB~,~AC}\) 上の点を \({\rm D~,~E}\) とするとき、

\({\small (1)}~\)\({\rm DE\,//\,BC}\) ならば、
\({\rm AD:AB=AE:AC=DE:BC}\)
※ \(\triangle {\rm ADE}\,\,\unicode{x223D}\,\,\triangle {\rm ABC}\) より、対応する辺の比が等しい。
※ \({\rm AB~,~AC}\) の延長線上に点 \({\rm D~,~E}\) があっても成り立つ。
\({\small (2)}~\)\({\rm DE\,//\,BC}\) ならば、
\({\rm AD:DB=AE:EC}\)

※ このとき、\({\rm DE:BC}\) は等しくないので注意!
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:三角形と線分の比
問題解説(1)
問題
\({\small (1)}~\)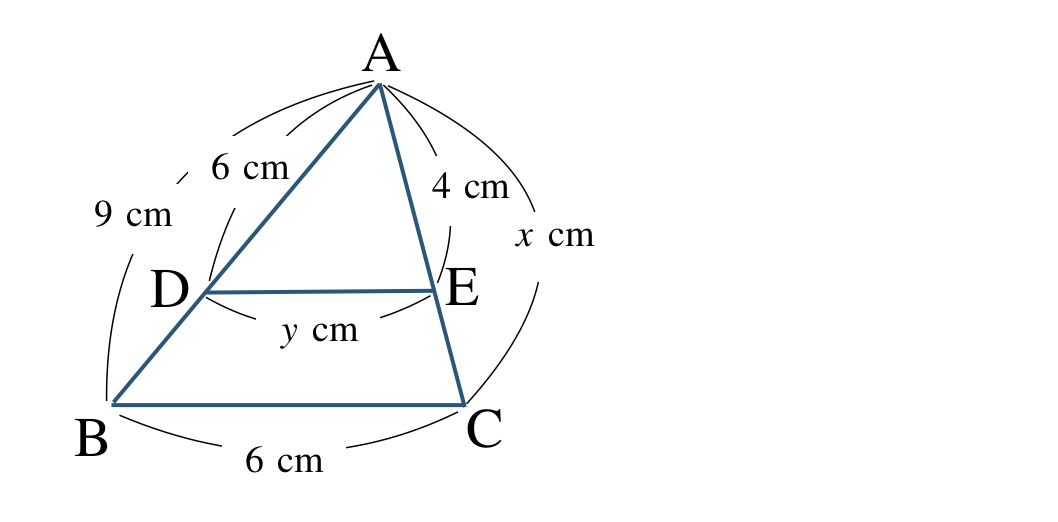
次の図で \({\rm BC\,//\,DE}\) のとき、\(x~,~y\) の値を求めよ。
\({\small (1)}~\)

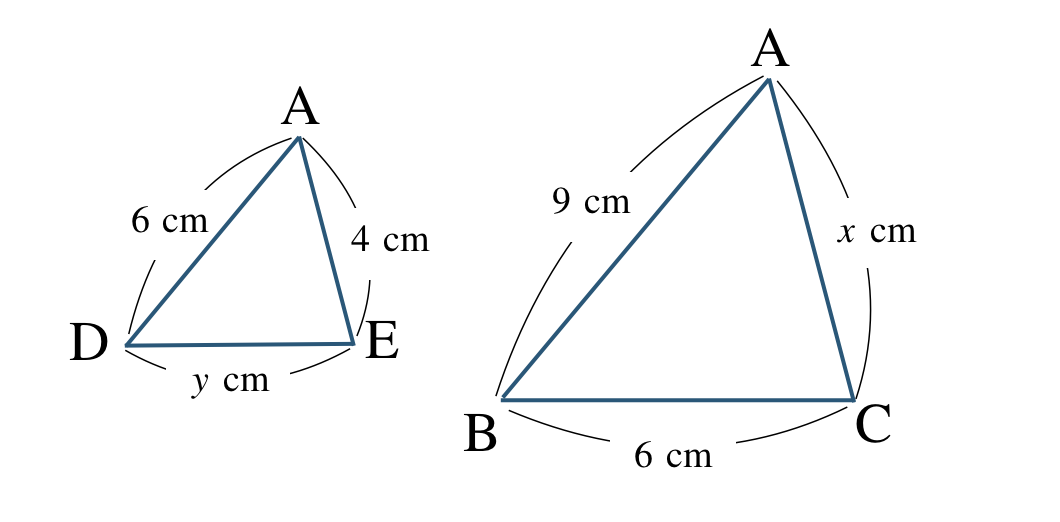
三角形と線分の比の定理より、
\({\rm AD:AB=AE:AC}\) が成り立つので、
\(\begin{eqnarray}~~~6:9&=&4:x\\[2pt]~~~6{\, \small \times \,} x&=&9{\, \small \times \,}4\\[2pt]~~~6x&=&36\\[3pt]~~~\frac{\,6x\,}{\,6\,}&=&\frac{\,36\,}{\,6\,}\\[3pt]~~~x&=&6~~{\rm cm}\end{eqnarray}\)
また、\({\rm AD:AB=DE:BC}\) が成り立つので、
\(\begin{eqnarray}~~~6:9&=&y:6\\[2pt]~~~9{\, \small \times \,} y&=&6{\, \small \times \,}6\\[2pt]~~~9y&=&36\\[3pt]~~~\frac{\,9y\,}{\,9\,}&=&\frac{\,36\,}{\,9\,}\\[3pt]~~~y&=&4~~{\rm cm}\end{eqnarray}\)
したがって、\(x=6~~{\rm cm}~,~y=4~~{\rm cm}\) となる
問題解説(2)
問題
\({\small (2)}~\)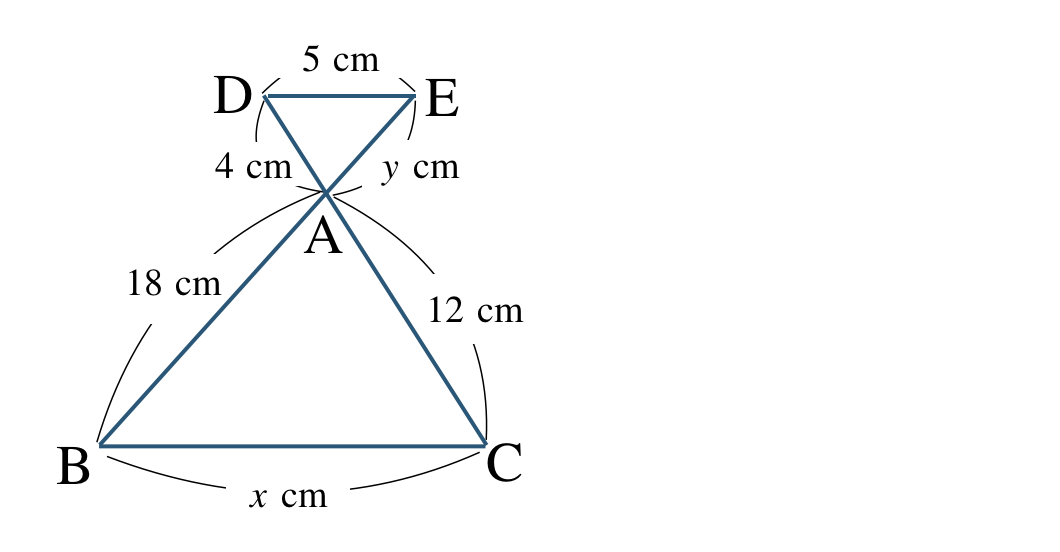
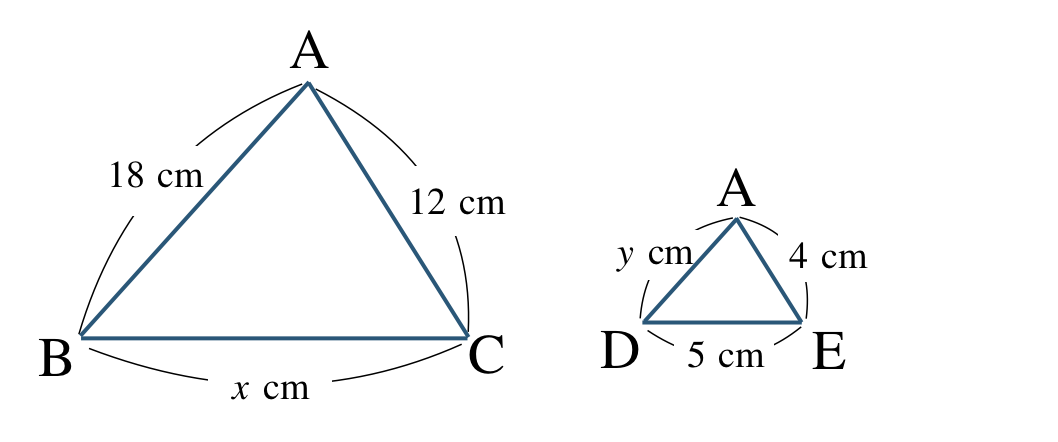
次の図で \({\rm BC\,//\,DE}\) のとき、\(x~,~y\) の値を求めよ。
\({\small (2)}~\)

\({\rm BC\,//\,DE}\) より、錯角が等しいから、
\(\angle{\rm ACB}=\angle{\rm AED}\)
対頂角が等しいから、
\(\angle{\rm BAC}=\angle{\rm DAE}\)
2組の角がそれぞれ等しいから、
\(\triangle {\rm ABC}\,\,\unicode{x223D}\,\,\triangle {\rm ADE}\)
相似な図形では、対応する辺の比がそれぞれ等しいから、
\({\rm AC:AE=BC:DE}\)
これより、
\(\begin{eqnarray}~~~12:4&=&x:5\\[2pt]~~~4{\, \small \times \,} x&=&12{\, \small \times \,}5\\[2pt]~~~4x&=&60\\[3pt]~~~\frac{\,4x\,}{\,4\,}&=&\frac{\,60\,}{\,4\,}\\[3pt]~~~x&=&15~~{\rm cm}\end{eqnarray}\)
また、\({\rm AB:AD=AC:AE}\) が成り立つので、
\(\begin{eqnarray}~~~18:y&=&12:4\\[2pt]~~~y{\, \small \times \,} 12&=&18{\, \small \times \,}4\\[2pt]~~~12y&=&72\\[3pt]~~~\frac{\,12y\,}{\,12\,}&=&\frac{\,72\,}{\,12\,}\\[3pt]~~~y&=&6~~{\rm cm}\end{eqnarray}\)
したがって、\(x=15~~{\rm cm}~,~y=6~~{\rm cm}\) となる
※ これより、点 \({\rm D~,~E}\) が辺 \({\rm AB~,~AC}\) の延長線上にある場合でも、三角形と線分の比の定理が成り立つことがわかる。
問題解説(3)
問題
\({\small (3)}~\)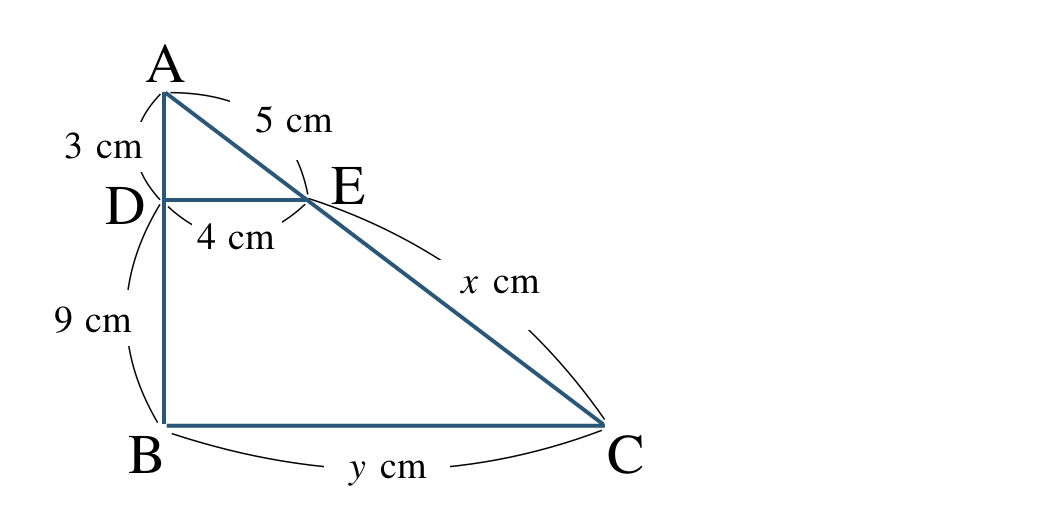
次の図で \({\rm BC\,//\,DE}\) のとき、\(x~,~y\) の値を求めよ。
\({\small (3)}~\)

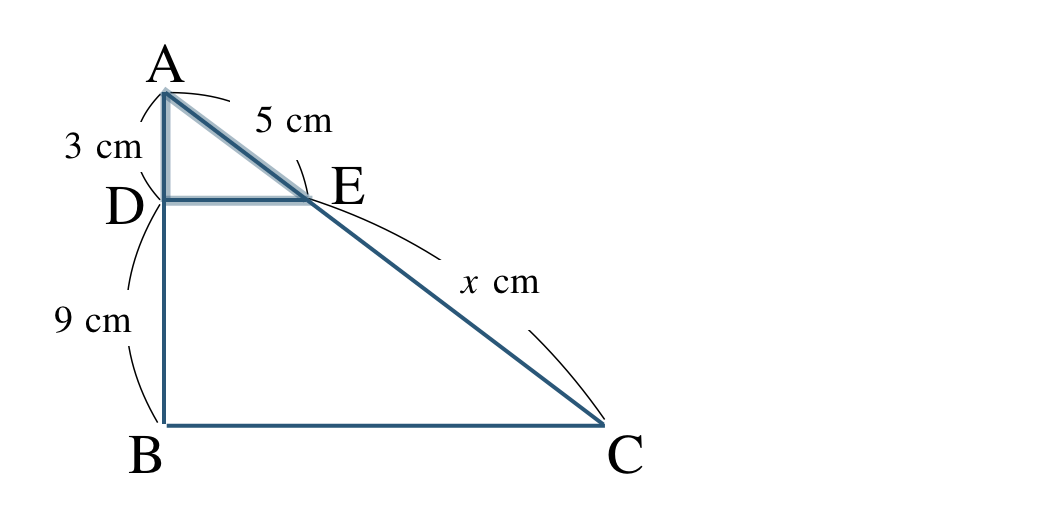
三角形と線分の比の定理より、
\({\rm AD:DB=AE:EC}\) が成り立つので、
\(\begin{eqnarray}~~~3:9&=&5:x\\[2pt]~~~3{\, \small \times \,} x&=&9{\, \small \times \,}5\\[2pt]~~~3x&=&45\\[3pt]~~~\frac{\,3x\,}{\,3\,}&=&\frac{\,45\,}{\,3\,}\\[3pt]~~~x&=&15~~{\rm cm}\end{eqnarray}\)
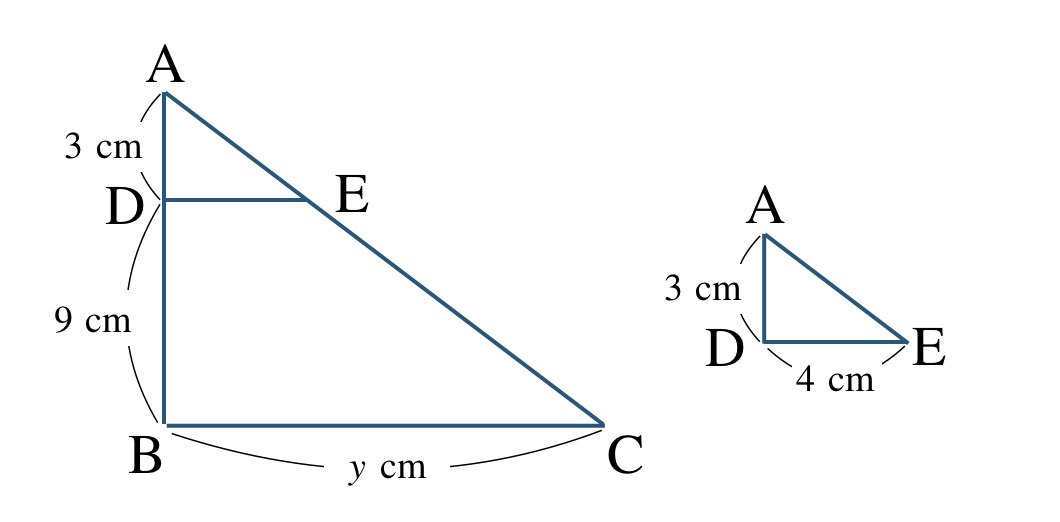
また、\({\rm AD:AB=DE:BC}\) が成り立つので、
\(\begin{eqnarray}~~~3:3+9&=&4:y\\[2pt]~~~3:12&=&4:y\\[2pt]~~~3{\, \small \times \,} y&=&12{\, \small \times \,}4\\[2pt]~~~3y&=&48\\[3pt]~~~\frac{\,3y\,}{\,3\,}&=&\frac{\,48\,}{\,3\,}\\[3pt]~~~y&=&16~~{\rm cm}\end{eqnarray}\)
したがって、\(x=15~~{\rm cm}~,~y=16~~{\rm cm}\) となる

【問題一覧】中3|相似な図形
このページは「中学数学3 相似な図形」の問題一覧ページとなります。解説の見たい単元名がわからないとき...


