三角形の線分の比と平行線の解法
\(\triangle {\rm ABC}\) の辺 \({\rm AB~,~AC}\) 上の点をそれぞれ \({\rm D~,~E}\) とするとき、
\({\small (1)}~\)\({\rm AD:AB=AE:AC}\) ならば、
\({\rm DE\,//\,BC}\)
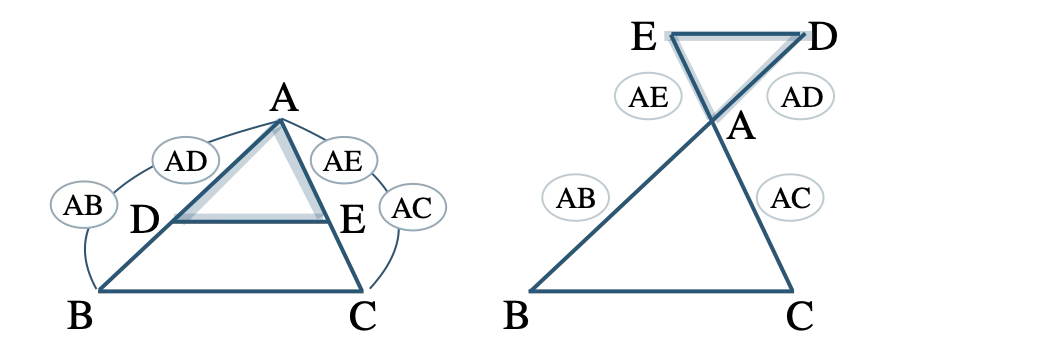
※ 2点 \({\rm D~,~E}\) が辺 \({\rm AB~,~AC}\) の延長線上にあるときも成り立つ。
\({\small (2)}~\)\({\rm AD:DB=AE:EC}\) ならば、
\({\rm DE\,//\,BC}\)
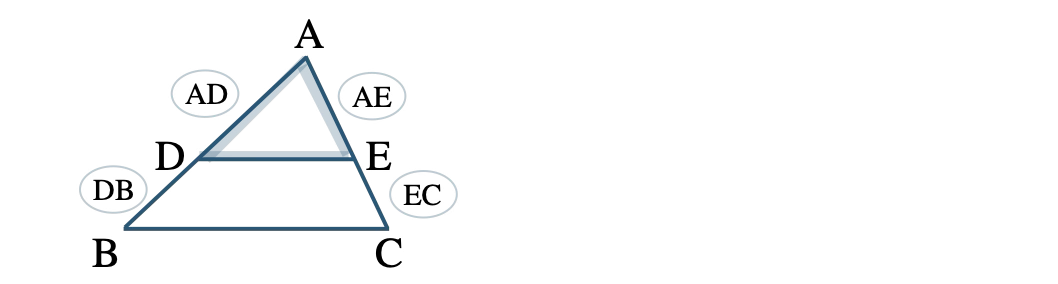
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:三角形の線分の比と平行線
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)次の \(\triangle {\rm ABC}\) において、
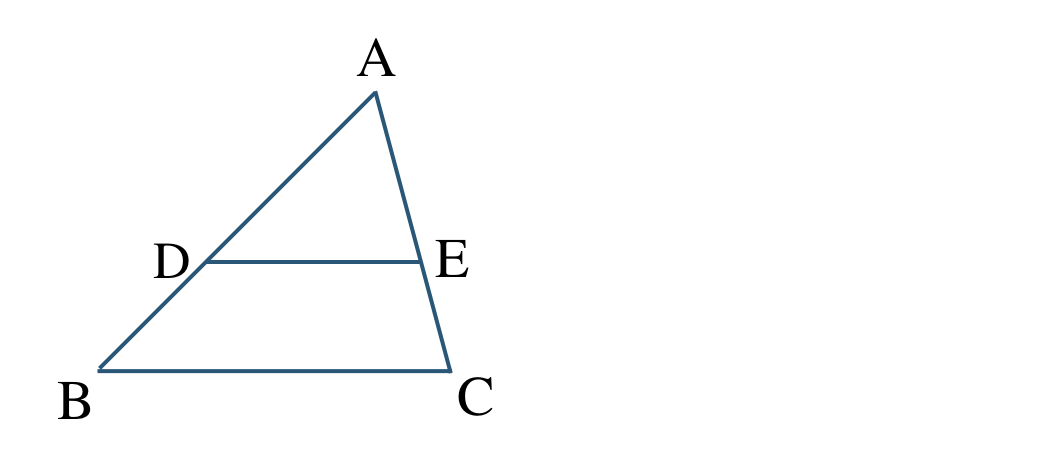
\({\rm AD:DB=AE:EC}=2:1\)
であるとき、次の問いに答えよ。
① \({\rm AD:AB}\) の比を求めよ。
② \({\rm BC}\) と \({\rm DE}\) の関係を答えよ。
③ \({\rm BC:DE}\) の比を求めよ。
① \({\rm AD:DB}=2:1\) より、$$\begin{split}&{\rm AD:AB}\\[2pt]~~=~&{\rm AD:AD+DB}\\[2pt]~~=~&2:2+1\\[2pt]~~=~&2:3\end{split}$$したがって、
\({\rm AD:AB}=2:3\)
となる
② 三角形と線分の比の定理の逆より、
\({\rm AD:DB=AE:EC}\)
であるので、
\({\rm DE\,//\,BC}\)
したがって、
線分 \({\rm BC}\) と \({\rm DE}\) は平行
である
③
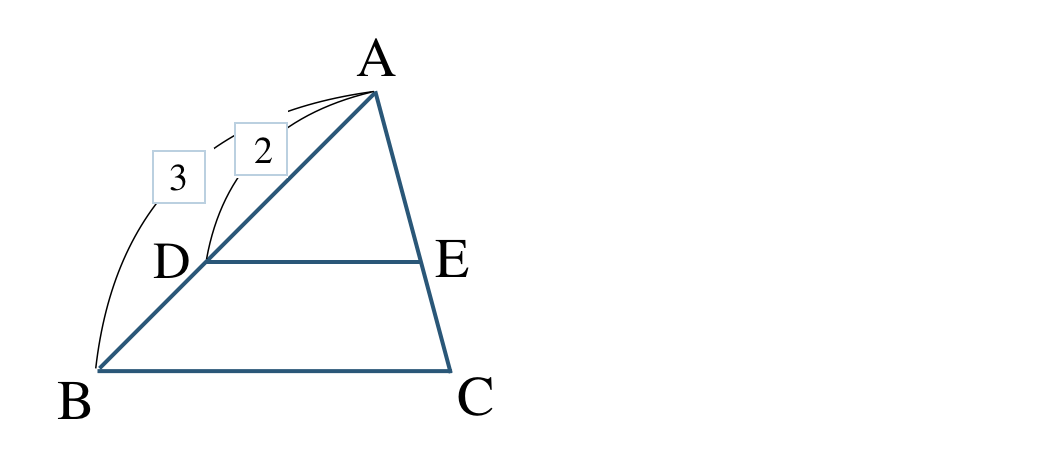
①より、\({\rm AB:AD}=3:2\) であるので、
三角形と線分の比の定理より、
\({\rm AB:AD=BC:DE}\)
したがって、
\({\rm BC:DE}=3:2\)
となる
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)次の \(\triangle {\rm ABC}\) において、線分 \({\rm DE~,~EF~,~FD}\) のうち、\(\triangle {\rm ABC}\) の辺と平行であるものを答えよ。
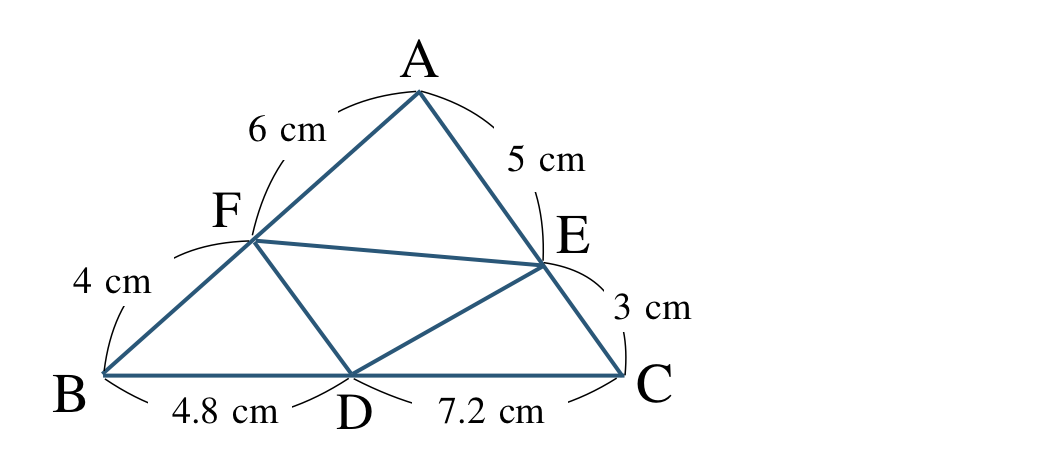
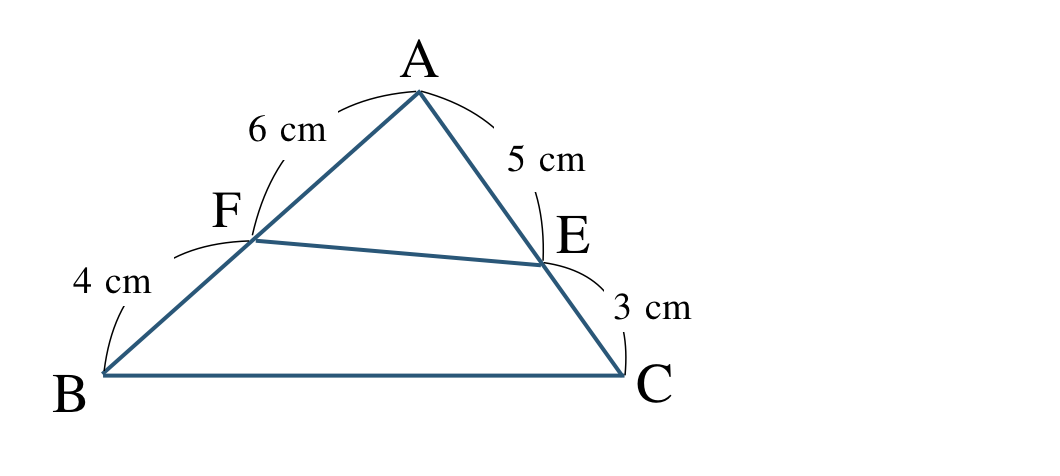
\(\triangle {\rm ABC}\) と線分 \({\rm FE}\) について、
\({\rm AF:FB}=6:4=3:2\)
\({\rm AE:EC}=5:3\)
これより、線分 \({\rm FE}\) と \({\rm BC}\) は平行でない
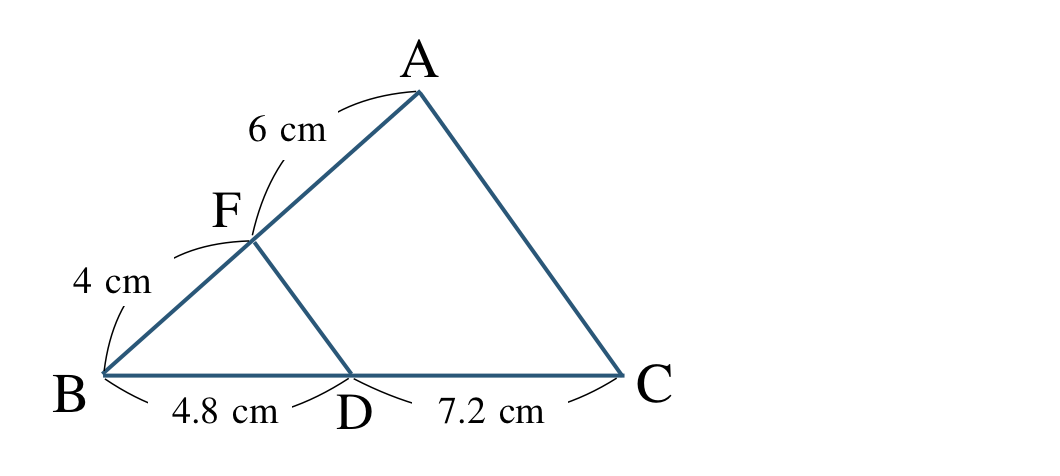
\(\triangle {\rm BAC}\) と線分 \({\rm FD}\) について、
\({\rm BF:FA}=4:6=2:3\)
\({\rm BD:DC}=4.8:7.2=2:3\)
これより、三角形の線分の比の定理の逆より、
\({\rm BF:FA=BD:DC}\) ならば \({\rm FD\,//\,AC}\)
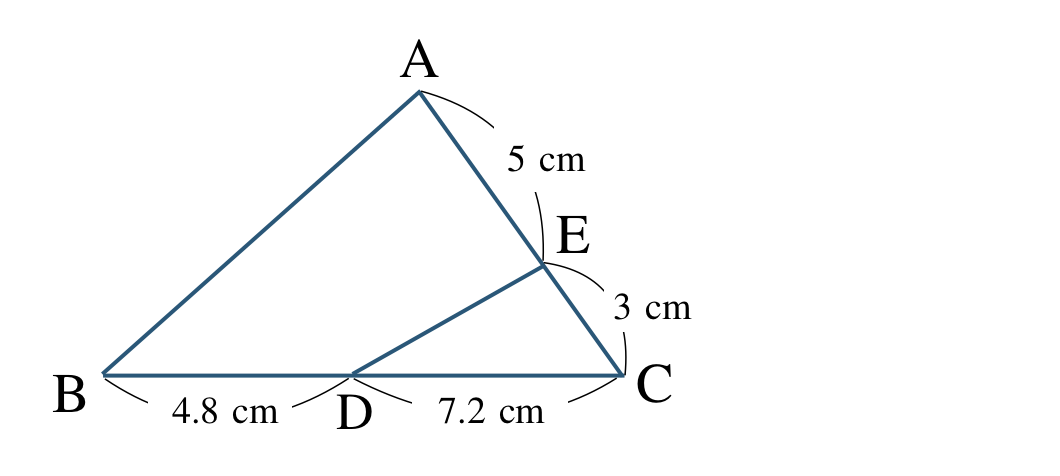
\(\triangle {\rm CAB}\) と線分 \({\rm ED}\) について、
\({\rm CE:EA}=3:5\)
\({\rm CD:DB}=7.2:4.8=3:2\)
これより、線分 \({\rm ED}\) と \({\rm AB}\) は平行でない
したがって、
辺 \({\rm AC}\) と線分 \({\rm FD}\) が平行である



