中点連結定理の利用の解法
四角形 \({\rm ABCD}\) の辺 \({\rm AB~,~BC~,~CD~,~DA}\) の中点がそれぞれ \({\rm E~,~F~,~G~,~H}\) であるとき、
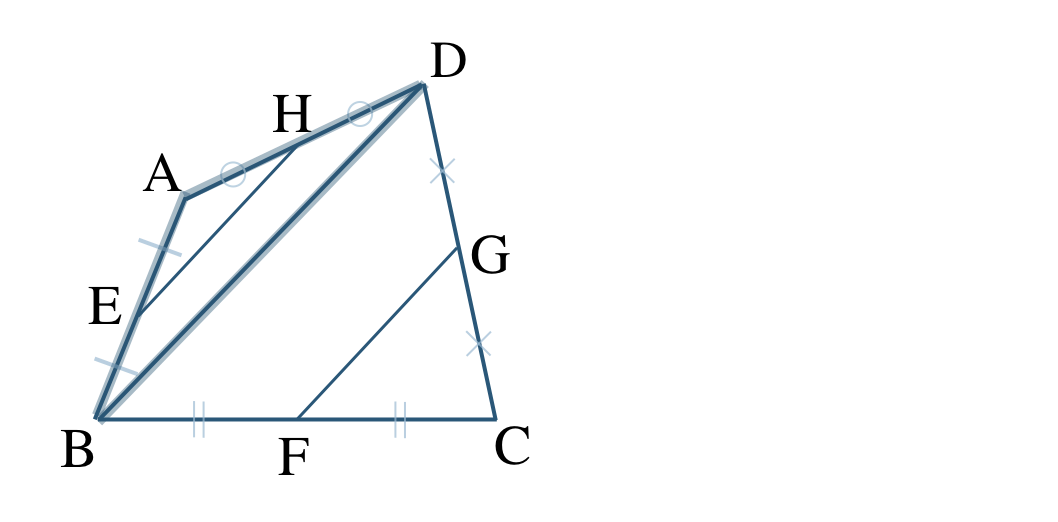
対角線を引くことで、2つの三角形に分けることができ、それぞれの三角形で中点連結定理を利用する。
\(\triangle {\rm ABD}\) で、\(\begin{split}{\rm EH\,//\,BD}~,~{\rm EH}=\frac{\,1\,}{\,2\,}{\rm BD}\end{split}\)
\(\triangle {\rm CBD}\) で、\(\begin{split}{\rm FG\,//\,BD}~,~{\rm FG}=\frac{\,1\,}{\,2\,}{\rm BD}\end{split}\)
これより、\(\begin{split}{\rm EH\,//\,FG~,~EH=FG}\end{split}\)
1組の対辺が等しくて平行であるので、
四角形 \({\rm EFGG}\) は平行四辺形である。
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:中点連結定理の利用
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)次の四角形 \({\rm ABCD}\) について、点 \({\rm E~,~F~,~G~,~H}\) がそれぞれ辺 \({\rm AB~,~BC~,~CD~,~DA}\) の中点であるとき、
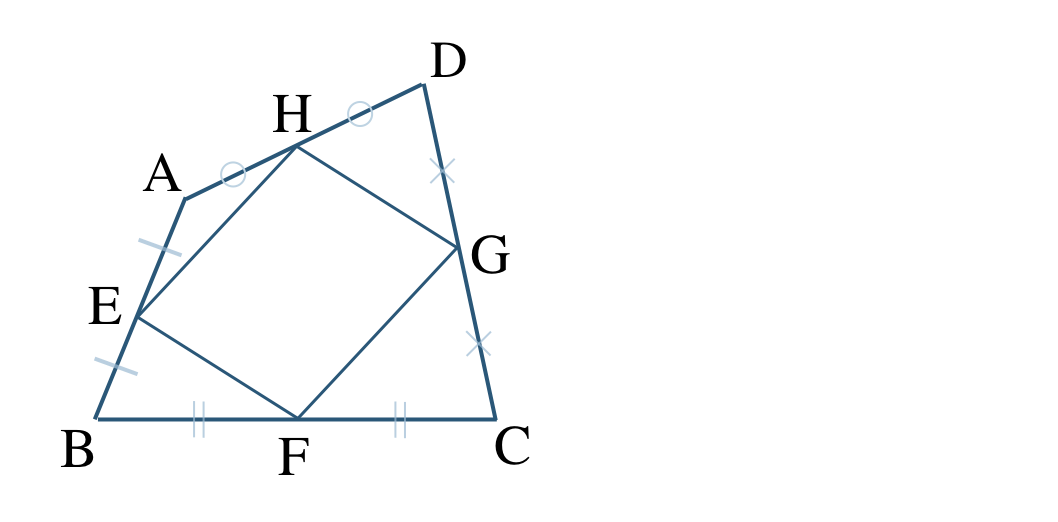
① 四角形 \({\rm EFGH}\) が平行四辺形であることを証明せよ。
② \({\rm AC=BD}\) のとき、四角形 \({\rm EFGH}\) はどのような四角形となるか答えよ。
③ 四角形 \({\rm ABCD}\) が長方形のとき、四角形 \({\rm EFGH}\) はどのような四角形となるか答えよ。
④ 四角形 \({\rm ABCD}\) がひし形のとき、四角形 \({\rm EFGH}\) はどのような四角形となるか答えよ。
① [証明] 対角線 \({\rm AC}\) を引くと、
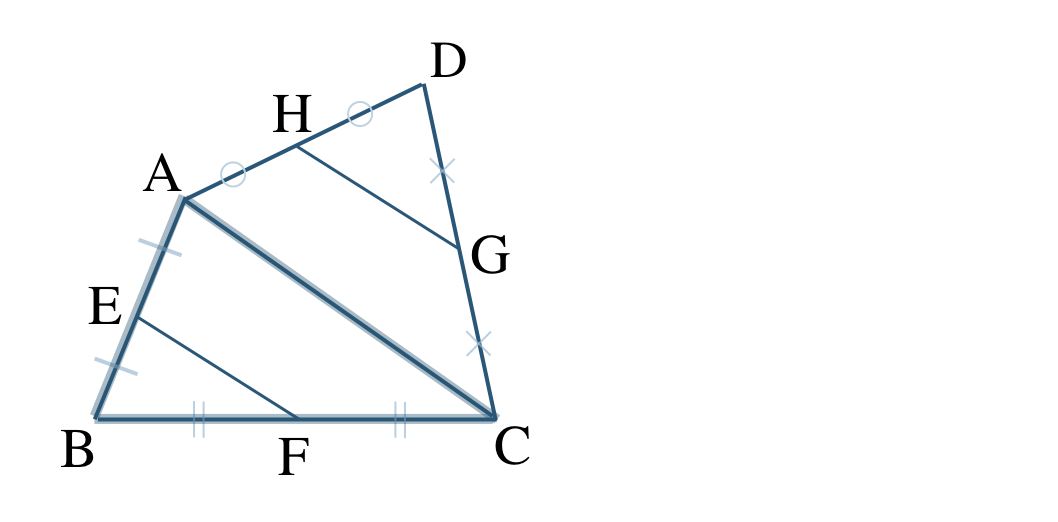
\(\triangle {\rm ABC}\) において、点 \({\rm E~,~F}\)はそれぞれ辺 \({\rm AB~,~BC}\) の中点であるので、中点連結定理より、
\(\begin{split}~~~{\rm EF\,//\,AC}~,~{\rm EF}=\frac{\,1\,}{\,2\,}{\rm AC}\end{split}\)
また、\(\triangle {\rm DAC}\) において、点 \({\rm H~,~G}\)はそれぞれ辺 \({\rm AD~,~CD}\) の中点であるので、中点連結定理より、
\(\begin{split}~~~{\rm HG\,//\,AC}~,~{\rm HG}=\frac{\,1\,}{\,2\,}{\rm AC}\end{split}\)
よって、\({\rm EF\,//\,AC}\) と \({\rm HG\,//\,AC}\) より、
\(\begin{split}~~~{\rm EF\,//\,HG}\end{split}\)
\(\begin{split}{\rm EF={ \frac{\,1\,}{\,2\,}}AC}\end{split}\) と \(\begin{split}{\rm HG={ \frac{\,1\,}{\,2\,}}AC}\end{split}\) より、
\(\begin{split}~~~{\rm EF=HG}\end{split}\)
これより、1組の対辺が等しくて平行であるので、
四角形 \({\rm EFGG}\) は平行四辺形である
[終]
② \({\rm AC=BD}\) のとき、
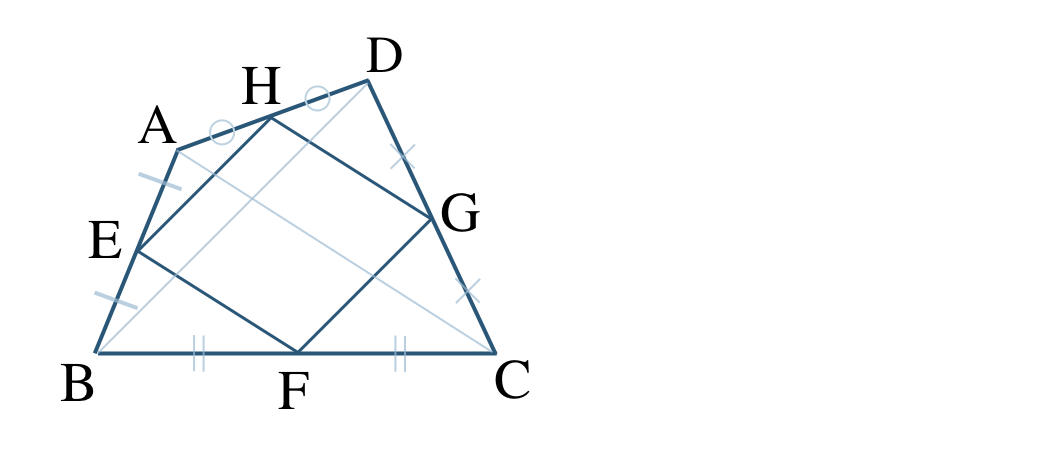
①より、
\(\begin{split}~~~{\rm EF=HG=\frac{\,1\,}{\,2\,}AC}\end{split}\)
また、対角線 \({\rm BD}\) でも同様に、
\(\begin{split}~~~{\rm EH=FG=\frac{\,1\,}{\,2\,}BD}\end{split}\)
\({\rm AC=BD}\) より、
\(\begin{split}~~~{\rm EF=HG=EH=FG}\end{split}\)
これより、平行四辺形の4つの辺の長さが等しいので、
四角形 \({\rm EFGH}\) はひし形となる
③ 長方形の対角線は等しいので、\({\rm AC=BD}\) となる
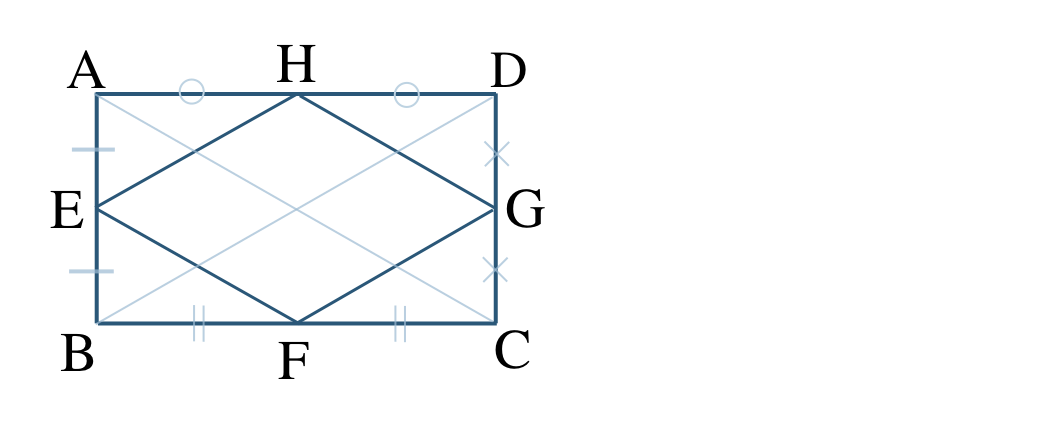
②と同じ条件となるので、
四角形 \({\rm EFGH}\) はひし形となる
④ 四角形 \({\rm ABCD}\) がひし形のとき、
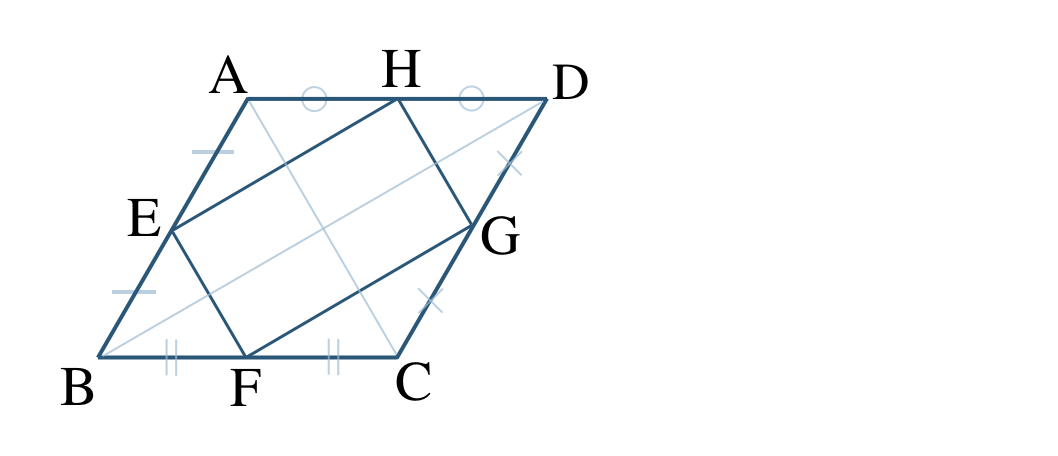
ひし形の対角線は垂直に交わるので、
\(\begin{split}~~~{\rm BD\perp AC}\end{split}\)
①より、\({\rm EF\,//\,AC}\)
対角線 \({\rm BD}\) でも同様に、\({\rm EH\,//\,BD}\)
よって、
\(\begin{split}~~~{\rm EF\perp EH}\end{split}\)
これより、平行四辺形 \({\rm EFGH}\) の1つの角が \(90^\circ\) であるので、
四角形 \({\rm EFGH}\) は長方形となる
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)次の四角形 \({\rm ABCD}\) について、点 \({\rm E~,~F}\) がそれぞれ辺 \({\rm AB~,~CD}\) の中点で、点 \({\rm P~,~Q}\) がそれぞれ対角線 \({\rm BD~,~AC}\) の中点であるとき、
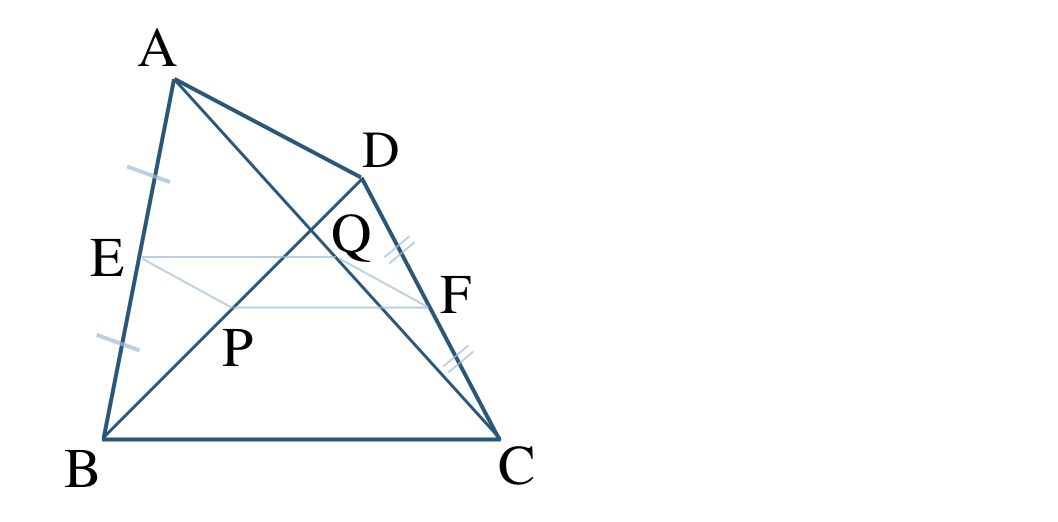
① 四角形 \({\rm EPFQ}\) が平行四辺形であることを証明せよ。
② \({\rm AD=BC}\) のとき、四角形 \({\rm EPFQ}\) はどのような四角形となるか答えよ。
① [証明]\(\triangle {\rm ABC}\) において、
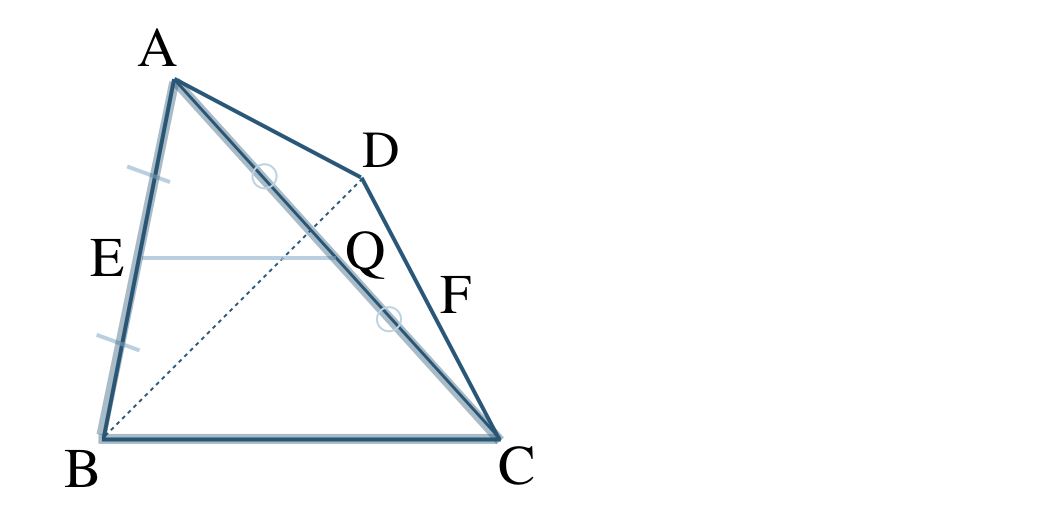
点 \({\rm E~,~Q}\)はそれぞれ辺 \({\rm AB~,~AC}\) の中点であるので、中点連結定理より、
\(\begin{split}~~~{\rm EQ\,//\,BC}~,~{\rm EQ}=\frac{\,1\,}{\,2\,}{\rm BC}\end{split}\)
また、\(\triangle {\rm DBC}\) において、
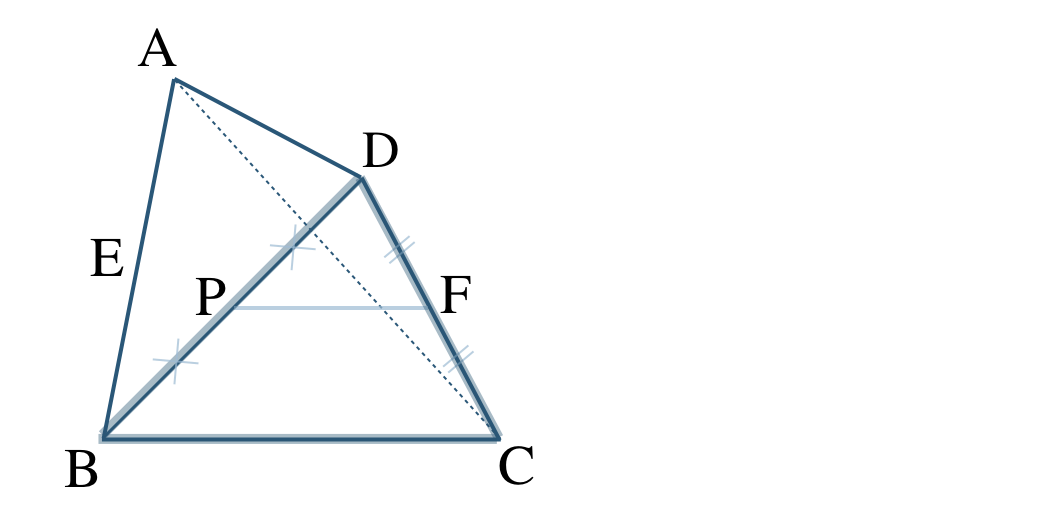
点 \({\rm P~,~F}\)はそれぞれ辺 \({\rm DB~,~DC}\) の中点であるので、中点連結定理より、
\(\begin{split}~~~{\rm PF\,//\,BC}~,~{\rm PF}=\frac{\,1\,}{\,2\,}{\rm BC}\end{split}\)
よって、\({\rm EQ\,//\,BC}\) と \({\rm PF\,//\,BC}\) より、
\(\begin{split}~~~{\rm EQ\,//\,PF}\end{split}\)
\(\begin{split}{\rm EQ={ \frac{\,1\,}{\,2\,}}BC}\end{split}\) と \(\begin{split}{\rm PF={ \frac{\,1\,}{\,2\,}}BC}\end{split}\) より、
\(\begin{split}~~~{\rm EQ=PF}\end{split}\)
これより、1組の対辺が等しくて平行であるので、
四角形 \({\rm EPFQ}\) は平行四辺形である
[終]
② \({\rm AD=BC}\) のとき、
①より、
\(\begin{split}~~~{\rm EQ=PF}=\frac{\,1\,}{\,2\,}{\rm BC}\end{split}\)
また、\(\triangle {\rm ABD}\) と \(\triangle {\rm ACD}\) でも同様に、
\(\begin{split}~~~{\rm EP=FQ}=\frac{\,1\,}{\,2\,}{\rm AD}\end{split}\)
\({\rm AD=BC}\) であるから、
\(\begin{split}~~~{\rm EQ=PF=EP=FQ}\end{split}\)
これより、平行四辺形の4つの辺の長さが等しいので、
四角形 \({\rm EPFQ}\) はひし形となる



