問題:平行線と線分の比
問題
\({\small (1)}~\)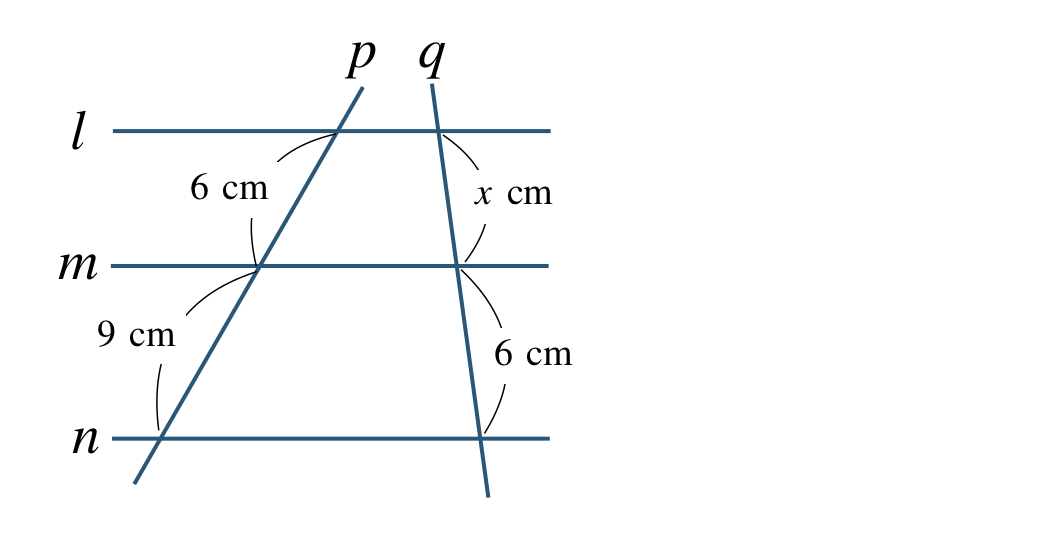
次の図で \(l\,//\,m\,//\,n\) であるとき、\(x\) の値を求めよ。
\({\small (1)}~\)

\({\small (2)}~\)

\({\small (3)}~\)

解法のPoint
Point:平行線と線分の比
平行な3直線 \(l~,~m~,~n\) に、
直線 \(p\) がそれぞれ点 \({\rm A~,~B~,~C}\) と交わり、
直線 \(q\) がそれぞれ点 \({\rm A’~,~B’~,~C’}\) と交わるとき、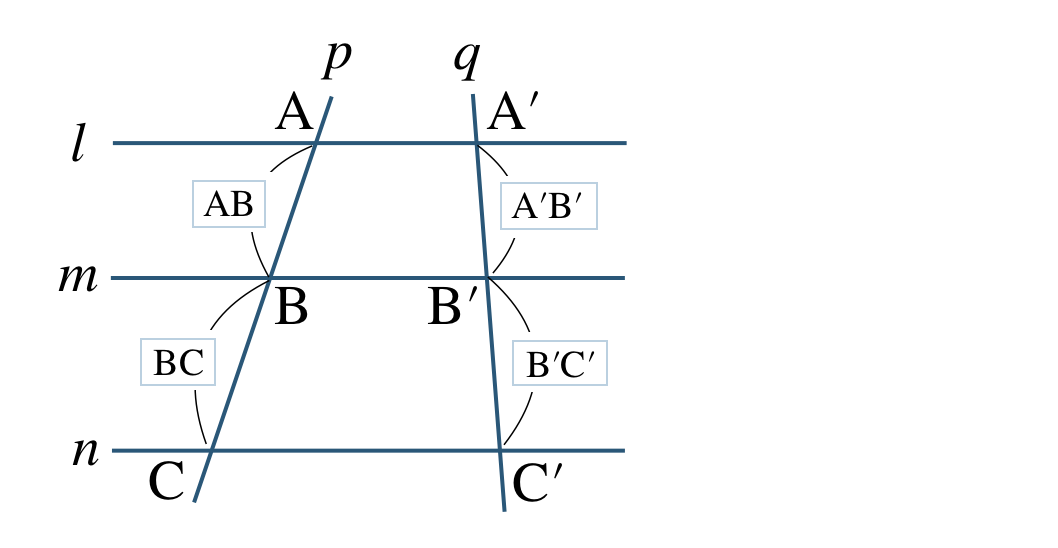
\({\rm AB:BC=A’B’:B’C’}\)
■ 平行線と線分の比
平行な3直線 \(l~,~m~,~n\) に、
直線 \(p\) がそれぞれ点 \({\rm A~,~B~,~C}\) と交わり、
直線 \(q\) がそれぞれ点 \({\rm A’~,~B’~,~C’}\) と交わるとき、

\({\rm A}\) と \({\rm A}\) が重なるように移動させると、
三角形と平行線の定理より、
\({\rm AB:BC=A’B’:B’C’}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:平行線と線分の比
問題解説(1)
問題
\({\small (1)}~\)
次の図で \(l\,//\,m\,//\,n\) であるとき、\(x\) の値を求めよ。
\({\small (1)}~\)

平行線と線分の比より、
\(\begin{eqnarray}~~~6:9&=&x:6\\[2pt]~~~9{\, \small \times \,} x&=&6{\, \small \times \,}6\\[2pt]~~~9x&=&36\\[3pt]~~~\frac{\,9x\,}{\,9\,}&=&\frac{\,36\,}{\,9\,}\\[3pt]~~~x&=&4~~{\rm cm}\end{eqnarray}\)
したがって、\(4~{\rm cm}\) となる
問題解説(2)
問題
\({\small (2)}~\)
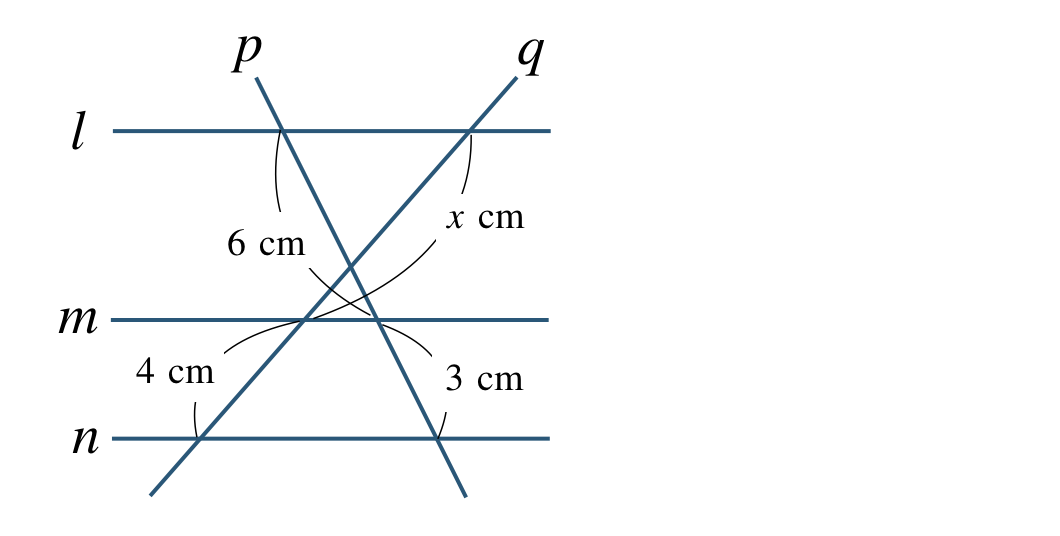
次の図で \(l\,//\,m\,//\,n\) であるとき、\(x\) の値を求めよ。
\({\small (2)}~\)

交わっている2直線 \(p~,~q\) を平行移動させると、
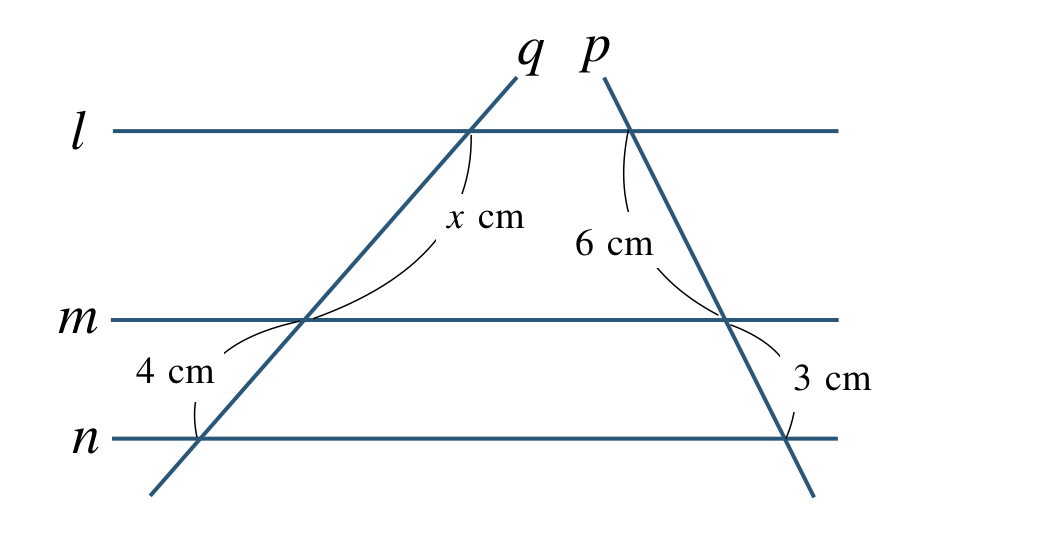
平行線と線分の比より、
\(\begin{eqnarray}~~~x:4&=&6:3\\[2pt]~~~x{\, \small \times \,} 3&=&4{\, \small \times \,}6\\[2pt]~~~3x&=&24\\[3pt]~~~\frac{\,3x\,}{\,3\,}&=&\frac{\,24\,}{\,3\,}\\[3pt]~~~x&=&8~~{\rm cm}\end{eqnarray}\)
したがって、\(8~{\rm cm}\) となる
問題解説(3)
問題
\({\small (3)}~\)
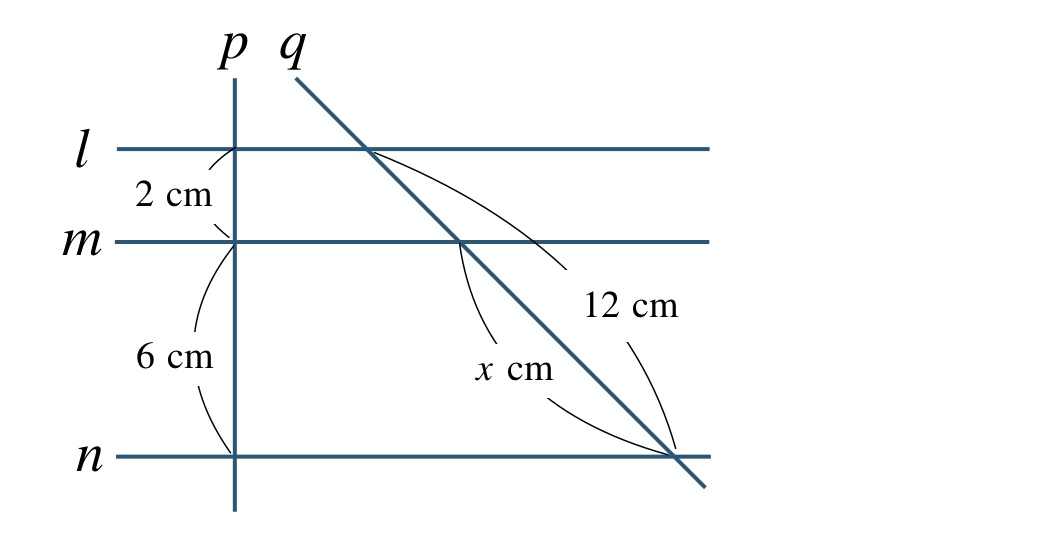
次の図で \(l\,//\,m\,//\,n\) であるとき、\(x\) の値を求めよ。
\({\small (3)}~\)

直線 \(q\) と直線 \(l~,~m\) の間の線分の長さは、
\(~~~12-x~~{\rm cm}\)
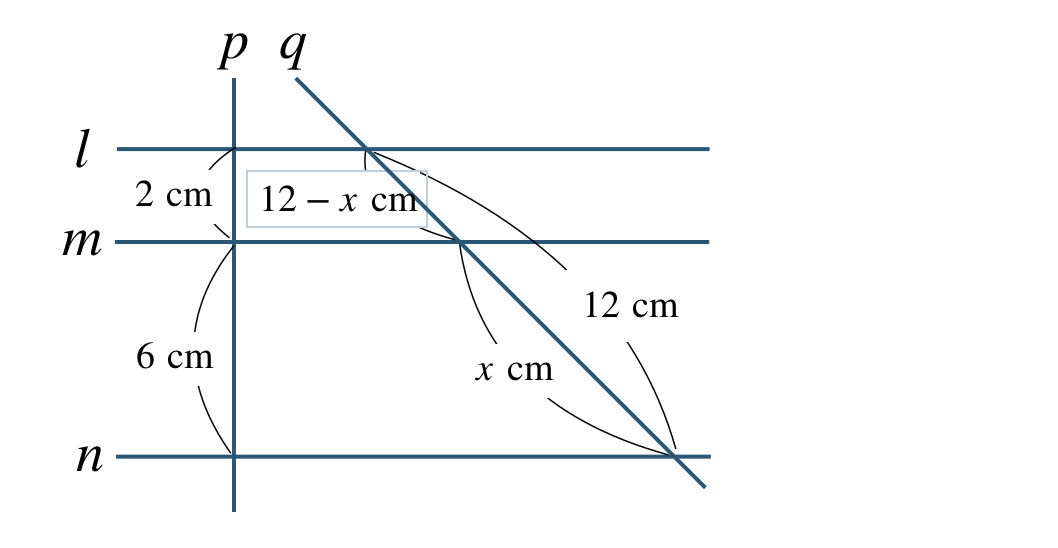
平行線と線分の比より、
\(\begin{eqnarray}~~~2:6&=&12-x:x\\[2pt]~~~2{\, \small \times \,} x&=&6{\, \small \times \,}(12-x)\\[2pt]~~~2x&=&6{\, \small \times \,}12+6{\, \small \times \,}(-x)\\[2pt]~~~2x&=&72-6x\\[2pt]~~~2x+6x&=&72\\[2pt]~~~8x&=&72\\[3pt]~~~\frac{\,8x\,}{\,8\,}&=&\frac{\,72\,}{\,8\,}\\[3pt]~~~x&=&9~~{\rm cm}\end{eqnarray}\)
したがって、\(9~{\rm cm}\) となる

【問題一覧】中3|相似な図形
このページは「中学数学3 相似な図形」の問題一覧ページとなります。解説の見たい単元名がわからないとき...


