問題:相似な図形の面積比
次の問いに答えよ。
\({\small (1)}~\)半径 \(6~{\rm cm}\) の円Aと半径 \(12~{\rm cm}\) の円Bにおいて、
① 相似比を求めよ。
② 面積比を求めよ。
\({\small (2)}~\)次の \(\triangle {\rm ABC}\) と \(\triangle {\rm ABC}\) が相似であるとき、
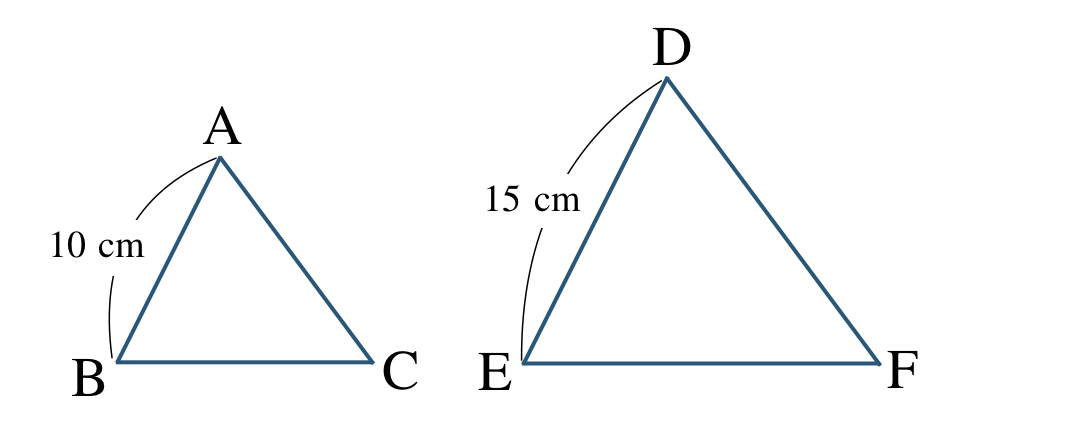
① 相似比を求めよ。
② 面積比を求めよ。
③ \(\triangle {\rm ABC}\) の面積が \(60~{\rm cm}^2\) のとき、\(\triangle {\rm DEF}\) の面積を求めよ。
\({\small (3)}~\)次の \(\triangle {\rm ABC}\) について、
\({\rm AD:DF:FB=2:1:1}\)
\({\rm BC\,//\,DE\,//\,FG}\)
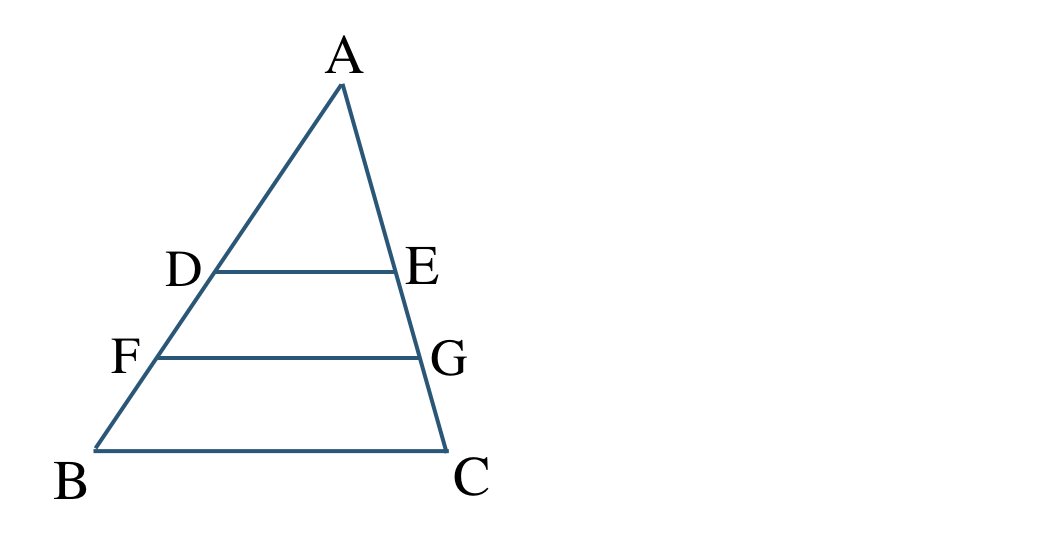
① \(\triangle {\rm ABC}\) と \(\triangle {\rm ADE}\) の面積比を求めよ。
② \(\triangle {\rm ABC}\) と \(\triangle {\rm AFG}\) の面積比を求めよ。
③ 台形 \({\rm DFGE}\) と台形 \({\rm FBCG}\) の面積比を求めよ。
\({\small (4)}~\)次の図形の面積比を求めよ。
① \(\triangle {\rm ABC}\) と \(\triangle {\rm DBC}\)
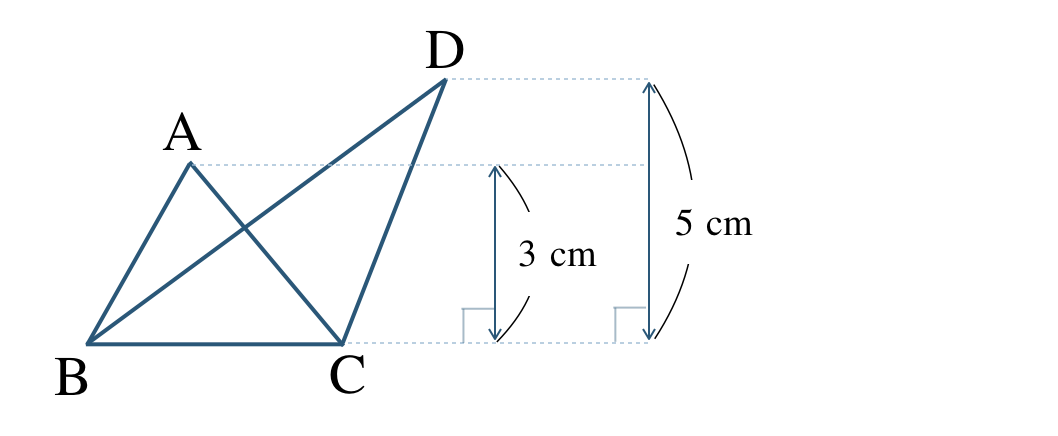
② \(\triangle {\rm ABC}\) と \(\triangle {\rm DEF}\)
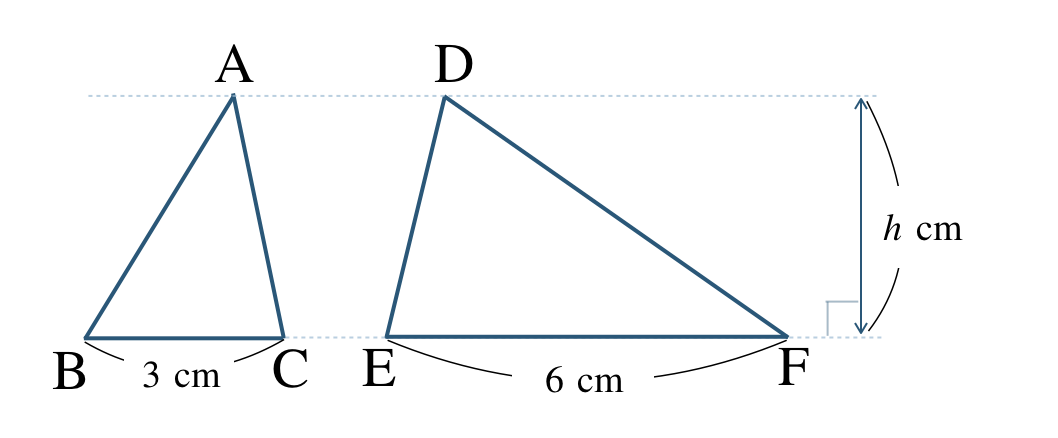
解法のPoint
\(\triangle {\rm ABC}\) と \(\triangle {\rm A’B’C’}\) の相似比が \(m:n\) であるとき、
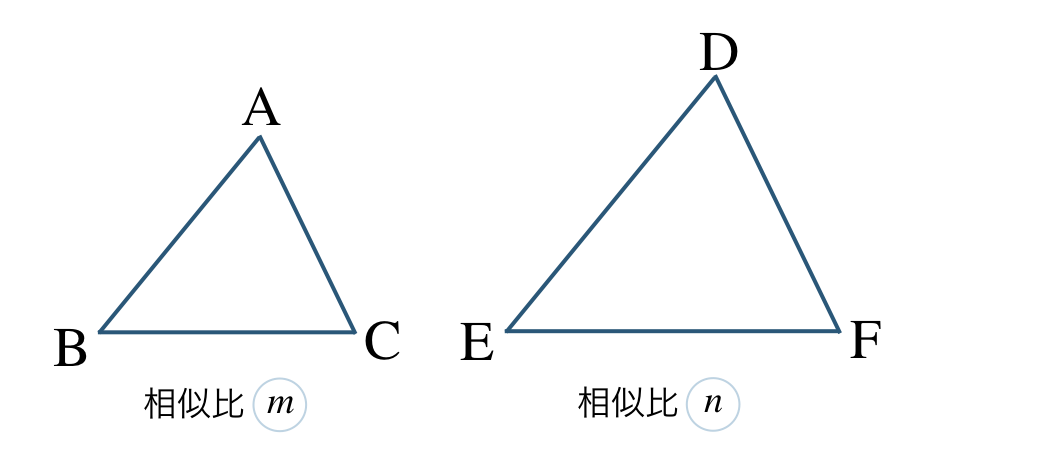
面積比は相似比の2乗に等しくなるので、
\(m^2:n^2\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
■ 底辺が等しい三角形の面積比
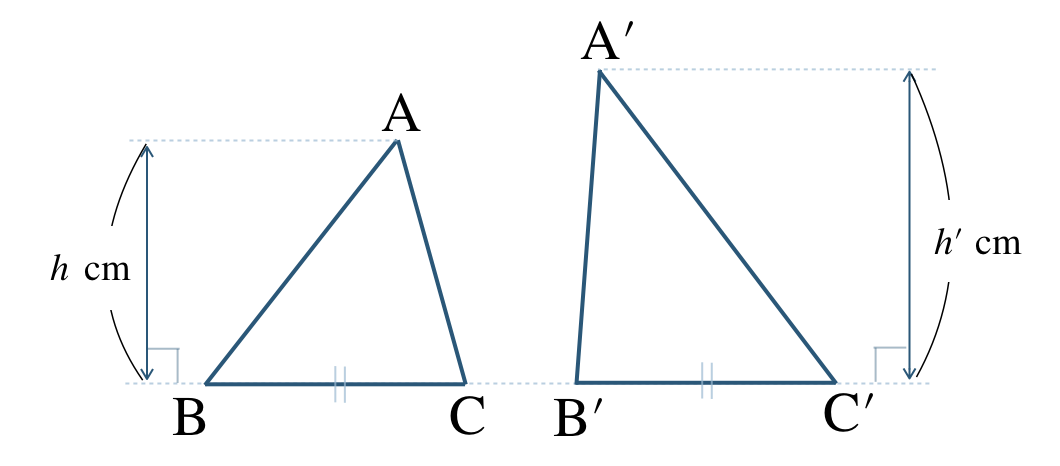
底辺 \({\rm BC=B’C’}\) で等しいので、高さの比が面積比となる。
\(h:h’\)
■ 高さが等しい三角形の面積比
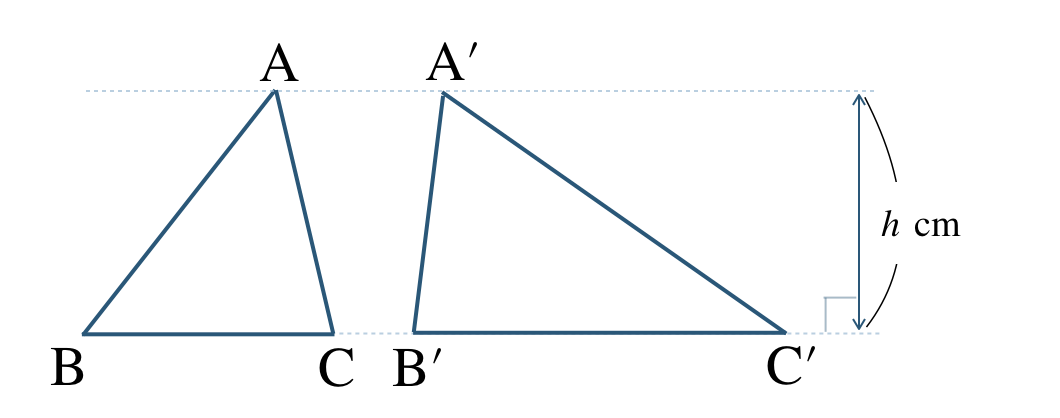
高さ \(h\) で等しいので、底辺の比が面積の比となる。
\({\rm BC:B’C’}\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:相似な図形の面積比
問題解説(1)
次の問いに答えよ。
\({\small (1)}~\)半径 \(6~{\rm cm}\) の円Aと半径 \(12~{\rm cm}\) の円Bにおいて、
① 相似比を求めよ。
② 面積比を求めよ。
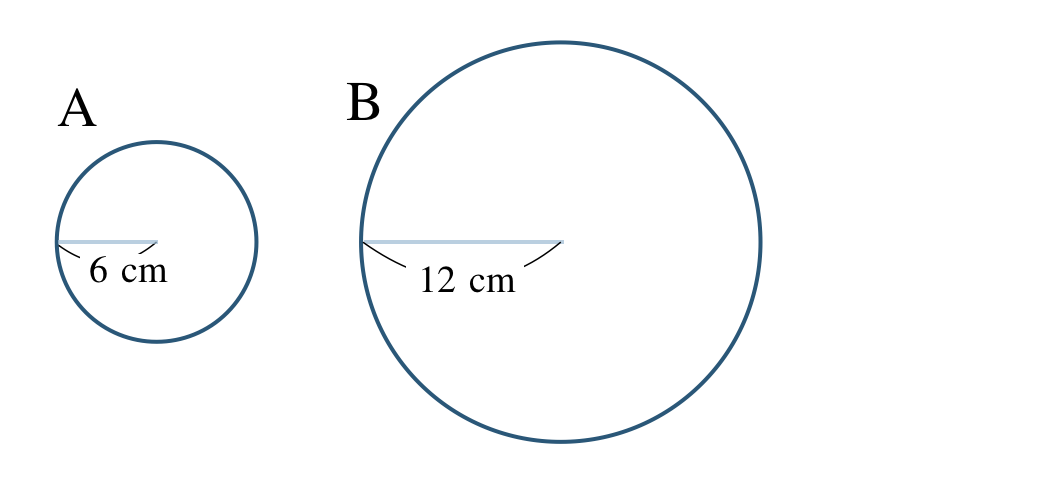
① 半径の比が相似比となるので、
\(~~~6:12=1:2\)
したがって、\(1:2\) となる
② 相似な図形の面積比は、相似比の2乗に等しいので、
\(~~~1^2:2^2=1:4\)
したがって、\(1:4\) となる
問題解説(2)
次の問いに答えよ。
\({\small (2)}~\)次の \(\triangle {\rm ABC}\) と \(\triangle {\rm ABC}\) が相似であるとき、

① 相似比を求めよ。
② 面積比を求めよ。
③ \(\triangle {\rm ABC}\) の面積が \(60~{\rm cm}^2\) のとき、\(\triangle {\rm DEF}\) の面積を求めよ。
①
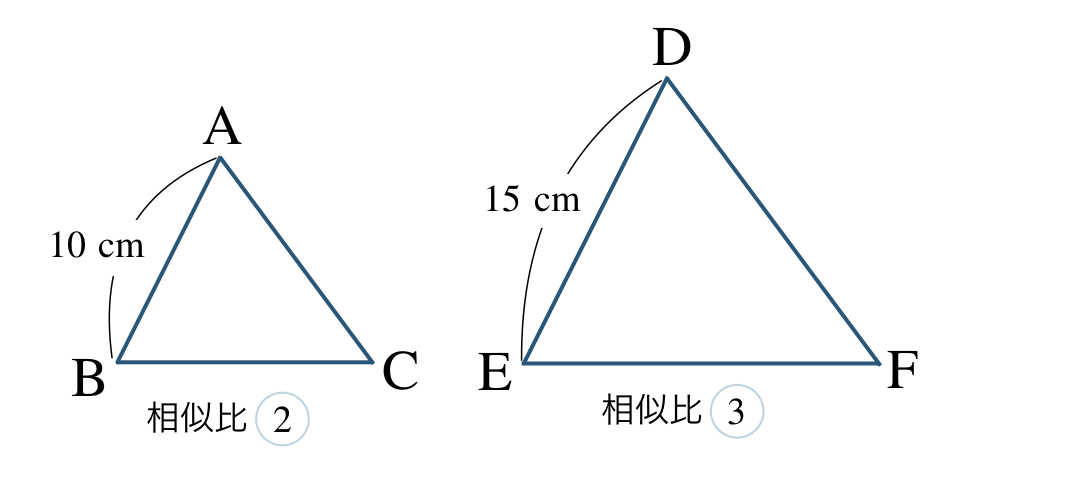
辺の比が相似比となるので、
\(~~~{\rm AB:DE}=10:15=2:3\)
したがって、\(2:3\) となる
② 相似な図形の面積比は、相似比の2乗に等しいので、
\(~~~2^2:3^2=149\)
したがって、\(4:9\) となる
③ \(\triangle {\rm DEF}\) の面積を \(x~{\rm cm}^2\) とすると、\(\triangle {\rm ABC}\) と \(\triangle {\rm ABC}\) の面積比が \(4:9\) より、
\(\begin{eqnarray}~~~60:x&=&4:9\\[2pt]~~~x\times 4&=&60\times9\\[2pt]~~~4x&=&540\\[3pt]~~~\frac{\,4x\,}{\,4\,}&=&\frac{\,540\,}{\,4\,}\\[3pt]~~~x&=&135\end{eqnarray}\)
したがって、\(135~{\rm cm}^2\) となる
問題解説(3)
次の問いに答えよ。
\({\small (3)}~\)次の \(\triangle {\rm ABC}\) について、
\({\rm AD:DF:FB=2:1:1}\)
\({\rm BC\,//\,DE\,//\,FG}\)
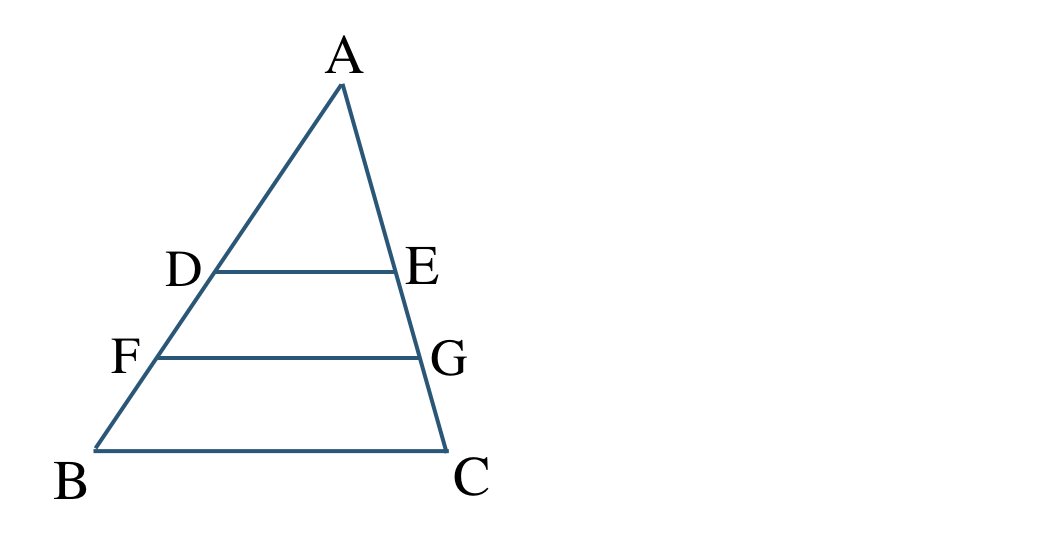
① \(\triangle {\rm ABC}\) と \(\triangle {\rm ADE}\) の面積比を求めよ。
② \(\triangle {\rm ABC}\) と \(\triangle {\rm AFG}\) の面積比を求めよ。
③ 台形 \({\rm DFGE}\) と台形 \({\rm FBCG}\) の面積比を求めよ。
① \(\triangle {\rm ABC}\) と \(\triangle {\rm ADE}\) において、
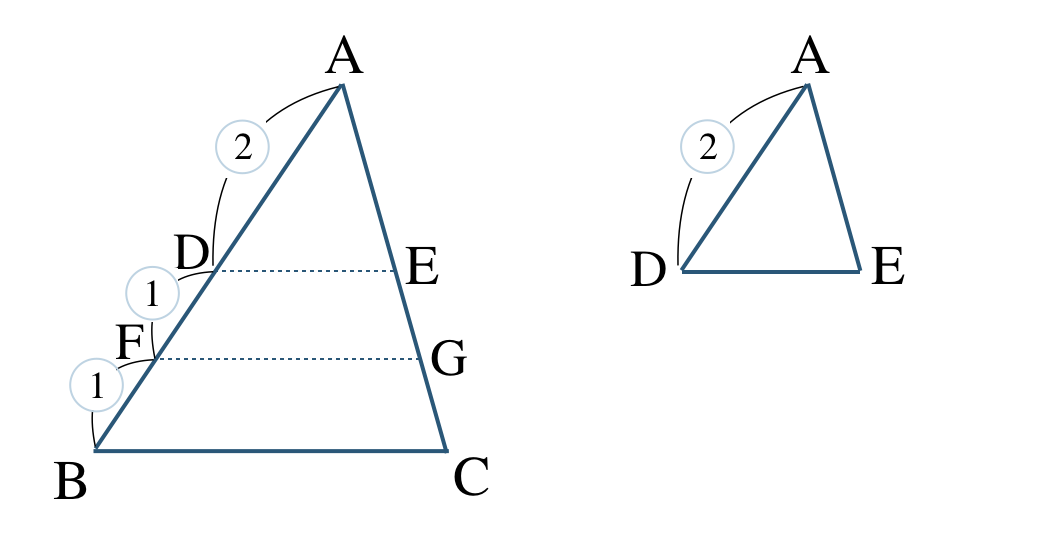
辺 \({\rm AB}\) と \({\rm AD}\) の比は、
\(\begin{eqnarray}~~~{\rm AB:AD}&=&2+1+1:2\\[2pt]~~~&=&4:2\\[2pt]~~~&=&2:1\end{eqnarray}\)
相似比が \(2:1\) となり、面積比はこれの2乗に等しいので、
\(~~~2^2:1^2=4:1\)
したがって、\(4:1\) となる
② \(\triangle {\rm ABC}\) と \(\triangle {\rm AFG}\) において、
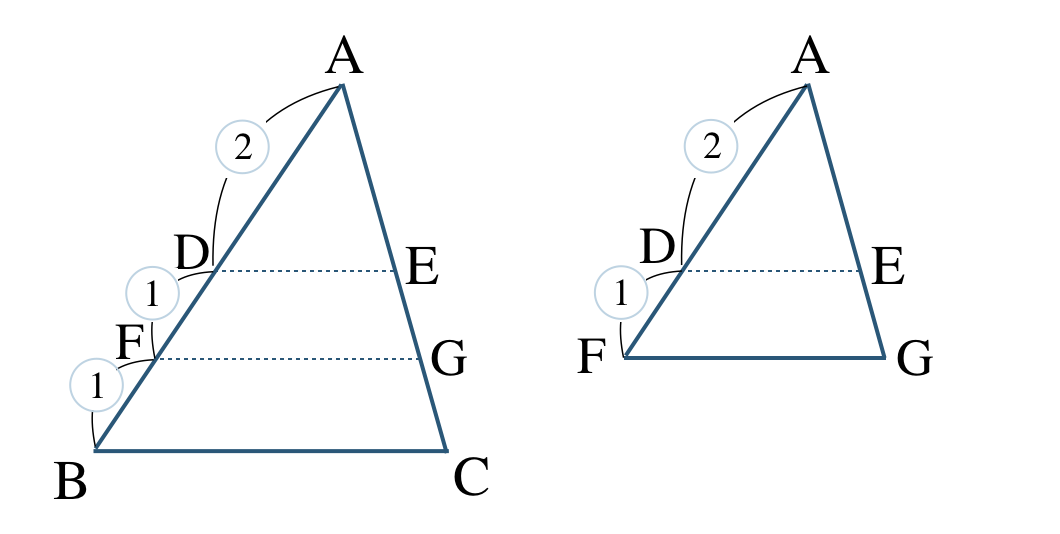
辺 \({\rm AB}\) と \({\rm AF}\) の比は、
\(\begin{eqnarray}~~~{\rm AB:AF}&=&2+1+1:2+1\\[2pt]~~~&=&4:3\end{eqnarray}\)
相似比が \(4:3\) となり、面積比はこれの2乗に等しいので、
\(~~~4^2:3^2=16:9\)
したがって、\(16:9\) となる
③ \(\triangle {\rm ABC}\) と \(\triangle {\rm ADE}\) の面積比は、
\(~~~4:1=16:4\)
\(\triangle {\rm ABC}\) と\(\triangle {\rm AFG}\) の面積比は、
\(~~~16:9\)
これより、\(\triangle {\rm ABC}\) と \(\triangle {\rm AFG}\) と \(\triangle {\rm ADE}\) の面積比は、
\(~~~16:9:4\)
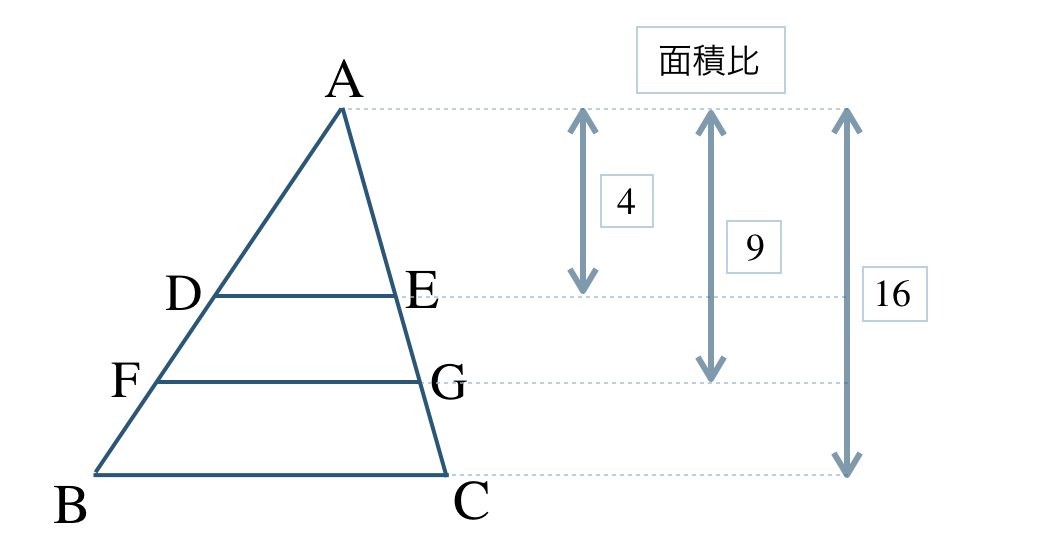
\(\triangle {\rm ABC}\) の面積比を \(16\) としたとき、
台形 \({\rm DBCE}\) の面積比は、
\(~~~16-4=12\)
台形 \({\rm FBCG}\) の面積比は、
\(~~~16-9=7\)
これより、台形 \({\rm DFGE}\) の面積比は、
\(~~~12-7=5\)
したがって、台形 \({\rm DFGE}\) と台形 \({\rm FBCG}\) の面積比は \(5:7\) となる
問題解説(4)
次の問いに答えよ。
\({\small (4)}~\)次の図形の面積比を求めよ。
① \(\triangle {\rm ABC}\) と \(\triangle {\rm DBC}\)

② \(\triangle {\rm ABC}\) と \(\triangle {\rm DEF}\)

① 底辺が \({\rm BC}\) で等しいので、面積比は高さの比となる
よって、
\(~~~\triangle {\rm ABC}:\triangle {\rm DBC}=3:5\)
したがって、\(3:5\) となる
② 高さが \(h\) で等しいので、面積比は底辺の比となる
よって、
\(~~~\triangle {\rm ABC}:\triangle {\rm DEF}=3:6=1:2\)
したがって、\(1:2\) となる



