問題:相似な立体の表面積比と体積比
問題
\({\small (1)}~\)半径 \(6~{\rm cm}\) の球Aと半径 \(10~{\rm cm}\) の球Bについて、
① 相似比を求めよ。
② 表面積比を求めよ。
③ 体積比を求めよ。
\({\small (2)}~\)相似な2つの立体P、Qについて、相似比が \(7:2\) であるとき、
① Pの表面積が \(147~{\rm cm}^2\) であるとき、Qの表面積を求めよ。
② Qの体積が \(40~{\rm cm}^3\) であるとき、Pの体積を求めよ。
\({\small (3)}~\)次の図の円すいを高さで2等分するように分けたとき、上の円すいをA、下の立体をBとすると、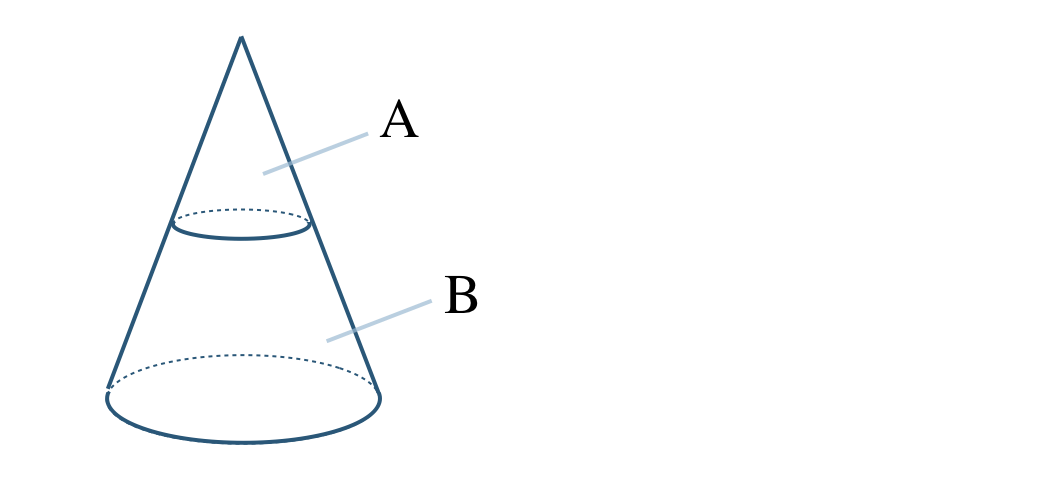
次の問いに答えよ。
\({\small (1)}~\)半径 \(6~{\rm cm}\) の球Aと半径 \(10~{\rm cm}\) の球Bについて、
① 相似比を求めよ。
② 表面積比を求めよ。
③ 体積比を求めよ。
\({\small (2)}~\)相似な2つの立体P、Qについて、相似比が \(7:2\) であるとき、
① Pの表面積が \(147~{\rm cm}^2\) であるとき、Qの表面積を求めよ。
② Qの体積が \(40~{\rm cm}^3\) であるとき、Pの体積を求めよ。
\({\small (3)}~\)次の図の円すいを高さで2等分するように分けたとき、上の円すいをA、下の立体をBとすると、

① もとの円すいと円すいAの体積比を求めよ。
② 円すいAと立体Bの体積比を求めよ。
③ もとの円すいの体積が \(96\pi~{\rm cm}^3\) のとき、立体Bの体積を求めよ。
解法のPoint
Point:相似な立体の表面積比と体積比

表面積比 \(m^2:n^2\)
体積比は、相似比の3乗に等しくなるので、
体積比 \(m^3:n^3\)
相似な2つの立体の相似比が \(m:n\) であるとき、

表面積比は、相似比の2乗に等しくなるので、
表面積比 \(m^2:n^2\)
体積比は、相似比の3乗に等しくなるので、
体積比 \(m^3:n^3\)
©︎ 2024 教科書より詳しい中学数学 jhs.yorikuwa.com
問題解説:相似な立体の表面積比と体積比
問題解説(1)
問題
\({\small (1)}~\)半径 \(6~{\rm cm}\) の球Aと半径 \(10~{\rm cm}\) の球Bについて、
① 相似比を求めよ。
② 表面積比を求めよ。
③ 体積比を求めよ。
次の問いに答えよ。
\({\small (1)}~\)半径 \(6~{\rm cm}\) の球Aと半径 \(10~{\rm cm}\) の球Bについて、
① 相似比を求めよ。
② 表面積比を求めよ。
③ 体積比を求めよ。
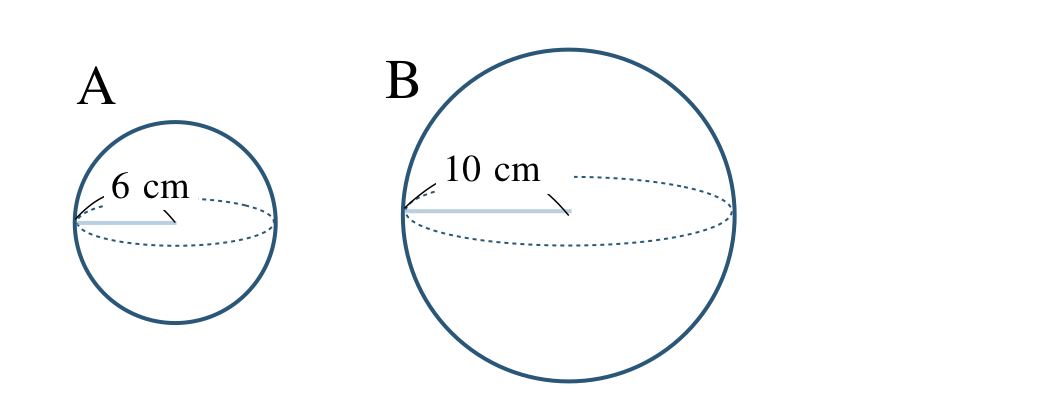
① 半径の比が相似比となるので、
\(~~~6:10=3:5\)
したがって、相似比は \(3:5\) となる
② 表面積比は、相似比 \(3:5\) の2乗に等しいので、
\(~~~3^2:5^2=9:25\)
したがって、表面積比は \(9:25\) となる
③ 体積比は、相似比 \(3:5\) の3乗に等しいので、
\(~~~3^3:5^3=27:125\)
したがって、体積比は \(27:125\) となる
問題解説(2)
問題
\({\small (2)}~\)相似な2つの立体P、Qについて、相似比が \(7:2\) であるとき、
① Pの表面積が \(147~{\rm cm}^2\) であるとき、Qの表面積を求めよ。
② Qの体積が \(40~{\rm cm}^3\) であるとき、Pの体積を求めよ。
次の問いに答えよ。
\({\small (2)}~\)相似な2つの立体P、Qについて、相似比が \(7:2\) であるとき、
① Pの表面積が \(147~{\rm cm}^2\) であるとき、Qの表面積を求めよ。
② Qの体積が \(40~{\rm cm}^3\) であるとき、Pの体積を求めよ。
① 表面積比は、相似比 \(7:2\) の2乗に等しいので、
\(~~~7^2:2^2=49:4\)
Pの表面積が \(147~{\rm cm}^2\) で、Qの表面積を \(S~{\rm cm}^2\) とすると、
\(\begin{eqnarray}~~~147:S&=&49:4\\[2pt]~~~S\times 49&=&147\times 4\\[3pt]~~~\frac{\,49S\,}{\,49\,}&=&\frac{\,147\times4\,}{\,49\,}\\[3pt]~~~S&=&3\times4\\[2pt]~~~S&=&12\end{eqnarray}\)
したがって、Qの表面積は \(12~{\rm cm}^2\) となる
② 体積比は、相似比 \(7:2\) の3乗に等しいので、
\(~~~7^3:2^3=343:8\)
Qの体積が \(40~{\rm cm}^2\) で、Pの体積を \(V~{\rm cm}^2\) とすると、
\(\begin{eqnarray}~~~V:40&=&343:8\\[2pt]~~~V\times 8&=&40\times 343\\[3pt]~~~\frac{\,8V\,}{\,8\,}&=&\frac{\,40\times343\,}{\,8\,}\\[3pt]~~~V&=&5\times343\\[2pt]~~~V&=&1715\end{eqnarray}\)
したがって、Pの体積は \(1715~{\rm cm}^3\) となる
問題解説(3)
問題
\({\small (3)}~\)次の図の円すいを高さで2等分するように分けたとき、上の円すいをA、下の立体をBとすると、
次の問いに答えよ。
\({\small (3)}~\)次の図の円すいを高さで2等分するように分けたとき、上の円すいをA、下の立体をBとすると、

① もとの円すいと円すいAの体積比を求めよ。
② 円すいAと立体Bの体積比を求めよ。
③ もとの円すいの体積が \(96\pi~{\rm cm}^3\) のとき、立体Bの体積を求めよ。
①
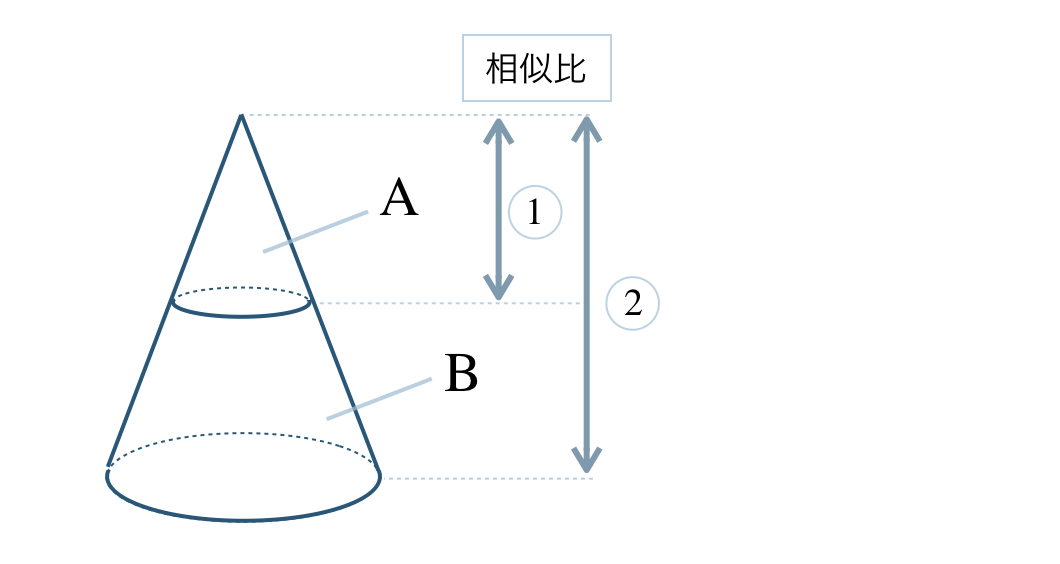
相似比が \(2:1\) より、体積比は相似比の3乗に等しいので、
\(~~~2^3:1^3=8:1\)
したがって、体積比は \(8:1\) となる
②
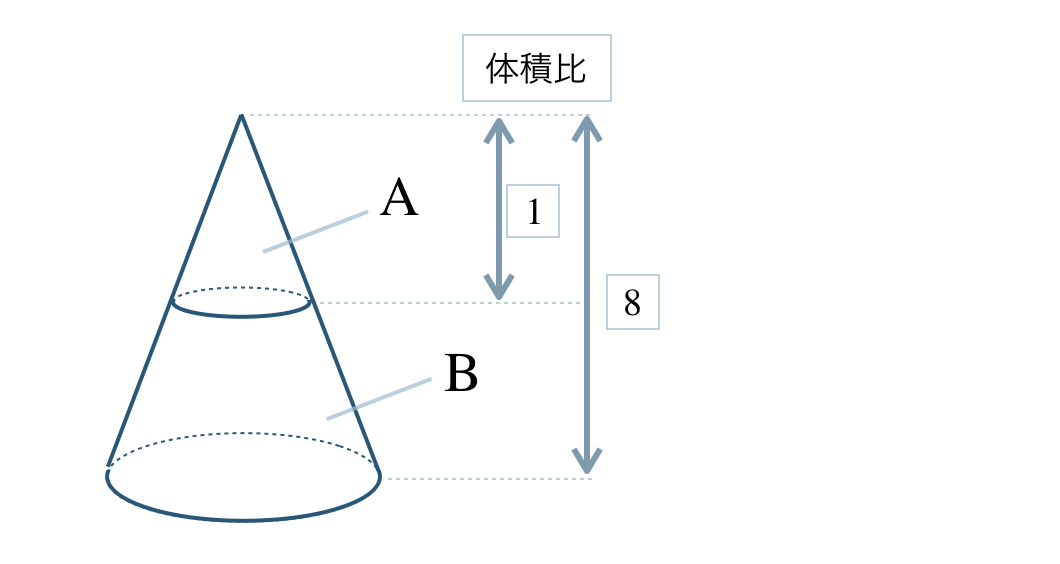
円すいAの体積比を \(1\) としたときの、立体Bの体積比は、
\(~~~8-1=7\)
したがって、円すいAと立体Bの体積比は \(1:7\) となる
③ もとの円すいの立体Bの体積比は、\(8:7\) である
立体Bの体積を \(x~{\rm cm}^3\) とすると、
\(\begin{eqnarray}~~~96\pi : x&=&8:7\\[2pt]~~~x\times 8&=&96\pi \times 7\\[3pt]~~~\frac{\,8x\,}{\,8\,}&=&\frac{\,96\pi \times 7\,}{\,8\,}\\[3pt]~~~x&=&12\pi \times7\\[2pt]~~~x&=&84\pi\end{eqnarray}\)
したがって、立体Bの体積は \(84\pi~{\rm cm}^3\) となる

【問題一覧】中3|相似な図形
このページは「中学数学3 相似な図形」の問題一覧ページとなります。解説の見たい単元名がわからないとき...


